Приближенный синтез Н∞ – регуляторов в нелинейных динамических системах на полубесконечном промежутке времени

Original Empirical Research

Approximate Synthesis of Н∞ – Controllers in Nonlinear Dynamic Systems over a Semi-Infinite Time Period

Andrei V. Panteleev , Aleksandra A. Yakovleva © H

Introduction . Problems and methods of finding Н ∞ – control are the basis of modern control theory. They are actively used to develop robust controllers, especially in aircraft control systems under limited external actions. These methods allow for adapting control systems to changing environmental conditions, which is critically important for providing the reliability and safety of aircraft operation. Current research is aimed at improving approaches to the synthesis of controllers covering both linear and nonlinear dynamic systems. In this context, special attention is paid to the integration of new mathematical methods, such as linear matrix inequalities and frequency analysis, which allows for optimizing the system response to various external actions and providing protection against unexpected conditions. It is important to note that, despite the progress made in this area, significant problems remain unsolved regarding the analysis and synthesis of controllers for nonlinear systems. This necessitates further research and development in this promising area. In this paper, in order to fill the existing gap, sufficient conditions for the existence of control for one of the frequently encountered classes of nonlinear systems are formulated and proven, which will then be used as a theoretical basis for developing approximate algorithms for finding it.

Информатика, вычислительная техника и управление

Materials and Methods . The basic research tool was the Н ∞ – control synthesis methods based on the minimax approach, which consisted in finding the control law under the worst external action. In this context, it was proposed to prove sufficient conditions for the existence of control using the extension principle. However, due to the computational difficulties that might arise when applying those conditions, it was decided to simplify the initial formulation of the problem. The simplification process was performed by approximate replacing the nonlinear system with another nonlinear system, which was similar in structure to the linear one, using the factorization procedure. This approach made it possible to use the solution of the Riccati equation, whose coefficients depended on the state vector, for the synthesis of controllers. To solve model examples and applied problems, a software package was developed using the MATLAB mathematical package.

Results . The article solved the problem of synthesis of Н ∞ – control of the state of nonlinear continuous dynamic systems, linear in control and disturbance. Sufficient conditions for the existence of Н ∞ – control were formulated and proved on the basis of the extension principle. An approximate method was proposed that provided solving the problem of finding control laws for dynamic systems that were nonlinear in state, similar to the methods used for linear systems. Analytical solutions were found for two model examples, which were illustrated by graphs of transient processes to demonstrate the results of numerical modeling of the considered nonlinear dynamic systems in the presence of external actions.

Discussion and Conclusion. The proposed approximate algorithm for synthesizing state and output controllers guarantees the required quality of transient processes and asymptotic stability of closed nonlinear control systems. This significantly expands the class of dynamic systems for which it is possible to synthesize controllers capable of resisting various external actions. The methods presented in this paper can be effectively applied to solve a variety of control problems, including the design of autopilots and automatic navigation systems for aircraft, even under conditions of limited external actions.

Введение. Методы современной теории управления играют важную роль в разработке сложных авиационнокосмических систем, обеспечивая их эффективное функционирование. Для достижения высокой производительности, устойчивости и эффективности таких систем необходимо разработать алгоритмы синтеза регуляторов, способных работать в условиях неопределенности описания внешних воздействий. Современной основой для их разработки являются метод пространства состояний, частотный анализ и подход на основе линейных матричных неравенств [1] . Для решения задач нахождения оптимального управления обычно применяются достаточные условия оптимальности в форме уравнения Беллмана и вытекающие из него соотношения в частных случаях. Для поиска Н ∞ – регуляторов могут быть использованы линейные матричные неравенства. Они применяются для определения существования регулятора, который удовлетворяет определенным критериям производительности и обеспечивает устойчивость системы к внешним воздействиям. Эти критерии обычно связаны с Н ∞ – нормой, которая является мерой чувствительности системы к внешним возмущениям. Суть проблемы заключается в нахождении такого регулятора, который минимизирует эту норму, обеспечивая при этом устойчивость системы и удовлетворение критерию качества управления. Метод решения основывается на нахождении экстремума выпуклой целевой функции, где условия представлены в виде линейных матричных неравенств [2] . Благодаря использованию данного метода имеется возможность свести решение сложных систем линейных и нелинейных алгебраических матричных уравнений определенного вида к решению задач выпуклой оптимизации. Однако решение линейных матричных неравенств может быть затруднительно при рассмотрении сложных технических задач.

Альтернативный метод, основанный на стохастическом минимаксе, представлен в анизотропийной теории стохастического робастного управления, описанной в [3] . Основная идея при использовании данного метода заключается в том, что робастность при стохастическом управлении достигается с помощью явного включения различных сценариев распределения шума в единый показатель качества, подлежащий оптимизации. Статистическая неопределенность выражается через энтропию, а показатель робастного качества выбирается таким образом, чтобы дать возможность количественно оценить способность системы подавлять наихудшее внешнее воздействие. Применение такого подхода для решения сложных систем взаимосвязанных уравнений требует разработки и использования специализированных алгоритмов.

Следует отметить, что методы Н ∞ – оптимизации находят применение при решении множества различных прикладных задач, например, управления самолетом [4] , вертолетом [5] , квадрокоптером [6] и мультиагентными системами [7] , стабилизации роботов [8] , проектирования ракетных двигателей [9] , где при сравнении с другими регуляторами данные методы показывают хорошие результаты и меньшее значение ошибок при наличии ограниченных возмущений. Также стоит упоминания их использование в задачах фильтрации [10] , оценивания вектора состояния [11] и проектирования нейронных сетей [12] . Таким образом, разработка и развитие Н ∞ – методов оптимизации является актуальной темой для исследований. Ранее авторами рассматривалась задачи синтеза Н ∞ – регулятора [13] и Н ∞ – наблюдателя [14] для линейных динамических систем, для решения которых использовались достаточные условия оптимальности на основе принципа расширения. Их применение позволило обосновать процедуры синтеза и, как следствие, сформировать пошаговые алгоритмы решения задач.

Несмотря на значительные достижения в данной области, ряд проблем, связанных с анализом и синтезом регуляторов для нелинейных систем, остаются нерешенными. В связи с этим, в настоящей работе рассматривается задача синтеза регуляторов для нелинейных динамических систем, линейных по управлению и возмущению, на полубесконечном промежутке времени. Целью исследования является формулировка и доказательство достаточных условий существования управления, что позволит не только создать основу для новых исследований и разработок, но и восполнить существующие пробелы в области знаний. В частности, в работе предусмотрено использование достаточных условий в качестве теоретического обоснования для формулировки приближенных алгоритмов поиска управления для рассматриваемого класса динамических систем. Для проверки эффективности предложенного алгоритма будет решено два модельных примера.

Материалы и методы. Пусть имеется математическая модель объекта управления

X ( t ) = f ( x ( t )) + B 1 ( x ( t )) w ( t ) + B 2 ( x ( t )) u ( t ), x (0) = 0 , (1)

и модель измерительной системы y (t) = C (x (t)) x (t),                                                         (2)

где x ∈ R ⁿ — вектор состояния, u ∈ R ^q — вектор управления, w ∈ R ^p — вектор внешних воздействий, y ∈ R ^m — вектор выхода, t ∈ T = [0, ∞) — текущее время, 0 — нулевая матрица-столбец размеров ( n × 1). Будем считать заданными непрерывно-дифференцируемую векторную функцию f ( x ) размеров ( n × 1), а также матричные функции B 1 ( x ) размеров ( n × p ), B 2 ( x ) размеров ( n × q ), C ( x ) размеров ( m × n ). Модель объекта описывается уравнением, нелинейным по состоянию, но линейным относительно управления и внешних воздействий.

Подразумевается, что:

• а)    w (.) ∈ L 2 [0, ∞), u (.) ∈ L 2 [0, ∞);

• б)    m ≤ n , rg С ( x ) = m ;

• в)    начало координат x ≡ 0 есть точка равновесия, т.е. f ( 0 ) = 0 ;

• г)    B 1 ( x ) ≠ O , B 2 ( x ) ≠ O ;

где O — нулевая матрица соответствующих размеров.

Определен показатель, описывающий текущее поведение модели объекта управления (1) с измерительной системой (2):

|| z ⁽ t )| |2 = y ⁽ t)^T S ⁽ x ⁽ t )) y ⁽ t) + u^{T (} t) Q ⁽ x ⁽ t )) u ⁽ t ),                                             ⁽³⁾

где для всех x ∈ Rn Q(x) > 0 — симметрическая положительно определенная квадратная матрица порядка q, а S(x) > 0 — симметрическая неотрицательно-определенная квадратная матрица порядка m. Функционал (3) явля- ется квадратичным по управлению, но неквадратичным по состоянию.

Заметим, что рассматриваются модели объекта и измерительной системы, матрицы в которых зависят от век- тора состояния.

Требуется обеспечить справедливость условия:

»             »

j | | z ( t )| |² dt    j [ y ( t ) ^T S ( x ( t )) y ( t ) + u^T ( t ) Q ( x ( t )) u ( t )] dt

X                              x

J | H ⁽ t )| P dt                    J I| ^{w (} t ) P dt

X j [ xT (t) CT (x (t)) S (x (t)) C (x (t)) x (t) + uT (t) Q (x (t)) u (t)] dt

X j wT (t) P (x (t)) w (t) dt где ∀ x ∈ Rn P(x) > 0 — симметрическая квадратная матрица порядка p, γ > 0 — некоторое число. В качестве дополнительного условия рассматривается необходимость выполнения свойства асимптотической устойчивости замкнутой системы «объект-регулятор». Заметим, что важно найти наименьшую величину параметра γ*, обеспечивающего сохранение требуемых свойств замкнутой системы. Это возможно лишь при одновременном выполнении условий минимизации числителя и максимизации знаменателя выражения (4).

Информатика, вычислительная техника и управление

Условие (4) перепишем в форме

X

I ( и , ^w ) = j [| z ( t )||2 - у² || ^w ( t )|| p ] dt =

X                                  0^{L                     J}                                                    (5)

= j [ x^T ( t ) C T ( x ( t )) S ( x ( t )) C x ( t ) + u^T ( t ) Q ( x ( t )) и ( t ) - y² w T ( t ) P ( x ( t )) w ( t ) ] dt < 0.

Это означает, что требуется обеспечить выполнение неравенства (5) при минимизации затрат на управление в условиях максимального противодействия внешних воздействий (возмущений).

Достаточные условия существования Н ∞ – регуляторов

Предположим, что известна функция V ( x ) ∈ C ¹( Rⁿ ). Определим функцию

T

R ( x , и , w ) = |----— | [ f ( x ) + B 1 ( x ) w + B 2 ( x ) и ] + x^TC^T ( x ) S ( x ) C ( x ) x +

Id x J

+ uTQ(x)и - у2 wTP(x)w, где 5 V (x) f d V (x)    d V (x) ] T

5 x    ^5 x , , 5 xn J

Теорема. Если существует функция V ( x ) ∈ C ¹( Rⁿ ), удовлетворяющая условиям V ( 0 ) = 0 и

R ( x , и *( x ), w *( x )) = min max R ( x , и , w ) = 0 V x e R n ,                             (7)

uw где u *(x) = - 1 Q“‘ (x)B2T (x) ^Vx-, w *(x) = Л P"‘ (x)B-T (x) ^Vx-,(8)

• 2               dx            2yд

а функция V ( x ) определяется решением уравнения с частными производными:

P-V^ 1 f ( x )-1 1^1 B ( x ) Q - ( x ) Bl ( x ) x + 22

xxx

+ 1 ( Vx) ¹ b _- ( x ) p -¹ ( x ) B - ( x ) ^{d V} ( x ⁾ + x^T C T ( x ) S ( x ) C ( x ) x = 0,

4y f дx J то условие (4) удовлетворяется.

Доказательство. Предположим, что условия теоремы выполняются. Найдем min max R(x, u, w) , применяя не-uw обходимые условия безусловного экстремума, поскольку ограничений на переменные u, w не наложено:

8R ( x , u , w )      _T     8 V ( x )

--- ---- = B 2 (x ) —--2 Q(x ) u = 0, д ux dR (x, u, w)     т .8 V (x)

— ----- = Bi (x) — - 2y P(x)w = 0. 8 w8x

Решая матричные уравнения, получаем:

u *(x) = -1Q(x)B2T (x) ^Vx-, w *(x) = 1-P P(x)BiT (x) ^V-Px-, 2               дx             2y где u*(x), w*(x) — структуры управления моделью объекта и внешним воздействием (возмущением).

• 2 R (x, U, w)                       n~

Так как справедливо ---- t ----= 2 Q ( x ) >  0 v x e R , то достаточные условия минимума по управлению вы-

• 8 u 8 u

полняются. Также справедливы достаточные условия, гарантирующие достижение максимума по внешнему воз-

• 2 R (x, u, w)        2

действию w , поскольку---- t ----= -²Y P ( x ) <  0 v x e R .

• 8 w' 8 w

В таком случае:

R ( x , u , w ) = R ( x , u * ( x ), w * ( x )) - Y 2 [ w - w * ( x )] T P ( x )[ w - w * ( x )] + [ u - u * ( x )] ^T Q ( x )[ u - u * ( x )].

Отсюда получим:

R ( x , u * ( x ), w ( x )) <  R ( x , u *( x ), w * ( x )) <  R ( x , u ( x ), w * ( x )),

т.е. выполняются условия наличия седловой точки.

Предположим, что функция V ( x ) ∈ C ¹( Rⁿ ) удовлетворяет условиям V ( 0 ) = 0 и R ( x , u *( x ), w *( x )) = 0.

Тогда справедливо соотношение, выполняющееся вдоль траекторий системы (1), а именно:

8 a V (x (t)) 1T fJ [f(x(t)) + Bi(x(t))w(x(t)) + B2(x(t))u(x(t))] + ||z(t)|| -y ||w(t)|P =

= dV ( x ( t ))

dt

^- Y²11 ^w ( t )| P = ^R ( ^x ( t ), ^u * ( ^x ( t )), ^w * ( ^x ( t ))) ^-4----------------------------V----------------------------'

-Y 2 [ w ( t ) - w * ( x ( t ))] ^T P ( x ( t ))[ w ( t ) - w * ( x ( t ))] + [ u ( t ) - u * ( x ( t ))] ^T Q ( x ( t )) [ u ( t ) - u * ( x ( t ))].

При u = u*(x) перепишем левую часть неравенства (10), т.е. R(x, u *(x), w(x)) < R(x, u *(x), w*(x)), в виде: V________________v________________/

dV ( x ( t )) dt

1² -Y²1| w ( t )| P < 0 .

Проинтегрировав левую и правую части полученного неравенства на промежутке времени от 0 до t 1 , получим:

t ₁

t ₁

V ( ^x ( t i ⁾⁾ - V ( ^{x (0))} + j | z ( t ⁾||² dt ^- Y² j 11 w ( t ⁾|[

I P < ⁰ .

Так как требуется обеспечить выполнение условия асимптотической устойчивости замкнутой системы, то x ( 1 1 ) ^ 0 при 1 1 ^ + м, поэтому V ( x ( 1 1 )) ^ V ( 0 ) = 0. Поскольку x (0) = 0 то V ( x (0)) ^ V ( 0 ) = 0. Отсюда можно сделать вывод о том, что при t 1 → + ∞ справедливо неравенство:

от                             от f||z(t)||2 dt < Y2 f|H(t)|Pddt, свидетельствующее о выполнении условия (4), что и требовалось доказать.

В качестве замечания подчеркнем, что при выполнении

от условий P(x) = E, j ||w(t)||2 dt < 1, т.е. ограниченности

от энергии внешних воздействий, справедливо неравенство вида j || z ( t )| |2 dt < у ² .

Приближенный синтез Н ∞ – регуляторов по состоянию методом SDRE

Вследствие нелинейности уравнения (9) и трудностей в получении его решения, для дальнейшего анализа применяется метод, основанный на алгебраическом уравнении Риккати с коэффициентами, зависящими от вектора состояния [15] .

В результате применения операции факторизации получим нелинейную систему, преобразованную к структуре, похожей на линейную, с матрицами, зависящими от вектора состояния.

Известно [16], что если f ( 0 ) = 0 и f ( x ) ∈ C ¹( Rⁿ ), то существует матричная функция A ( x ), такая что:

f ( x ) = A ( x ) x .                                                   (11)

Замечания

• 1.    Процедура факторизации для n = 1 единственная V x ^ 0 , т.е. A ( x ) = f(x ) / x = a ( x ).

• 2.    При n > 1 процедура факторизации дает неединственный результат [16]. Например, при n = 2 имеются, по крайней мере, два варианта: f ( x ) = A 1 ( x ) x и f ( x ) = A 2 ( x ) x , т.е. для системы вида:

( x A ( ^f .^{( x} ) A

I l =         1 + B 1 ⁽ x ) ^{W +} B 2 ^{( x} ) u .

I ^x 2 J I ^f 2 ⁽ x ) J

Получаем:

' f i x ) 0'

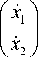
₀ Pxl'

x 2

₀ px).

x 2 J W

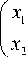
+ B 1 ( x ) w + B ₂ ( x ) u .

x        ( x 1 у

+ B (x) w + B2 (x)u или f2 (x) 0 Ix 2 J            2^

X ^x 1         J

Aw

3. Если имеются два варианта параметризации, т.е. f ( x ) = A 1 ( x ) x = A 2 ( x ) x , то имеется бесконечное семейство вариантов вида [16]: A ( x , α) = α A 1 ( x ) + (1 – α) A 2 ( x ) ∀ α. Выбор параметра α позволяет обеспечить гибкость при проектировании системы управления. Решение уравнения Риккати и соответствующее управление становятся функциями этого параметра.

В результате факторизации математическая модель системы (1) принимает вид:

x ( t ) = A ( x ( t )) x ( t ) + B 1 ( x ( t )) w ( t ) + B 2 ( x ( t )) u ( t ), x (0) = 0 .                                 (12)

На траекториях системы (12) задан функционал (5).

Предполагается, что система (12) является управляемой и наблюдаемой, т.е. ∀ x ∈ Rⁿ поточечно выполняются условия [16]:

rg[B2 (x) A(x)B2 (x)... An-1 (x)B2 (x)] = n , rg[CT (x) AT (x)CT (x) ... (AT (x))n-1 CT (x)] = n.

Уравнение (9) принимает вид:

у A(x)x -1 ^VW A B2 (x)Q-1 (x)BT (x) ^Ш + xx   x

₊ 1 p V ( x ) у ^T 4у² ^5 x J

B 1 ( x ) P -¹ ( x ) B 1 ^T ( x ) ^d V ( ^{x )} cx

+ x^TC^T ( x ) S ( x ) C ( x ) x = 0.

Предположим, что:

^ V ^ x ) = 2 K ₂ ( x ) x , dx        ²

Информатика, вычислительная техника и управление

где K 2 ( x ) > 0 — неизвестная матричная функция (при фиксированном x ∈ Rⁿ матрица K 2 ( x ) является симметрической положительно определенной числовой матрицей). Таким образом, делается предположение не о виде функции V ( x ), а только о структуре ее частной производной.

Тогда структуры управления объектом и возмущением принимают вид:

u *( x ) = -¹ Q-‘ ( x ) B 2 T ( x ) ^ Vx- = - Q - 1 ( x ) B 2 T ( x ) K 2 ( x ) x ,

• 2               d x

w *^{( x} ) = 717 ^P "‘^{( x} ) B i T ^{( x} ) Vx)- = Л ^P ~‘^{( x} ) B 1 T ^{( x} ) ^K 2^{( x} ) ^x . 2 y ²                  d x      у ²

Уравнение (13) принимает вид:

2 x T K ₂ ( x ) A ( x ) x - x T K ₂ ( x ) B ₂ ( x ) Q ^{- 1} ( x ) B T ( x ) K ₂ ( x ) x +

+ xT K 2 (x) B1 (x ) P 1-1 (x) Bi (x ) K2 (x ) x + xTCT (x) S (x ) C (x ) x = 0, Y или xT[2K2 (x)A(x) - K2 (x)B2 (x)Q~1 (x)BT(x)K2 (x) + -1 K2 (x)B1 (x)P^1 (x)B1T (x)K2 (x) + CT (x)S(x)C(x)]x = 0. Y

Применяя операцию транспонирования, получаем:

x^T [2 A T ( x ) K ₂ ( x ) - K ₂ ( x ) B ₂ ( x ) Q -¹ ( x ) B T ( x ) K ₂ ( x ) + -1- K ₂ ( x ) B 1 ( x ) P -1 ( x ) B 1 ^T ( x ) K ₂ ( x ) + C^T ( x ) S ( x ) C ( x )] x = 0. Y

Суммируя два последних выражения, приходим к равенству:

x^T [2 K ₂ ( x ) A ( x ) + 2 A^T ( x ) K ₂ ( x ) - 2 K ₂ ( x ) B ₂ ( x ) Q - 1 ( x ) B T ( x ) K ₂ ( x ) +

+ -- K ₂ ( x ) B 1 ( x ) P 1 ( x ) B 1 ^T ( x ) K ₂ ( x ) + 2 C^T ( x ) S ( x ) C ( x )] x = 0,

Y или окончательно:

x^T [ K ₂ ( x ) A ( x ) + A T ( x ) K ₂ ( x ) - K ₂ ( x ) B ₂ ( x ) Q ^{- 1} ( x ) B T ( x ) K ₂ ( x ) + + -1- K ₂ ( x ) B 1 ( x ) P ^- ( x ) B 1 ^T ( x ) K ₂ ( x ) + C^T ( x ) S ( x ) C ( x )] x = 0.

Заметим, что в силу зависимости всех матриц от вектора состояния, из (16) не следует равенство нулевой матрице выражения в квадратных скобках.

По аналогии со случаем линейной стационарной системы предлагается решать алгебраическое уравнение Риккати, все матрицы в котором являются функциями вектора состояния системы (State Dependent Riccati Equation, SDRE). При этом ищется положительно определенное решение уравнения Риккати, порождающее закон управления, гарантирующий то, что система будет асимптотически устойчива в окрестности положения равновесия. Для проверки этого свойства используется критерий устойчивости по корням характеристического уравнения, проверяемый поточечно, или критерий Рауса-Гурвица.

В рассматриваемой задаче предлагается решать уравнение:

K ₂ ( x ) A ( x ) + A^T ( x ) K ₂ ( x ) - K ₂ ( x ) [ B ₂ ( x ) Q ^-1 ( x ) B ₂ ^T ( x ) - -L B 1 ( x ) P ⁴ ( x ) B ^ ( x )] K ₂ ( x ) + C^T ( x ) S ( x ) C ( x ) = O ,   (17)

Y т.е. искать матрицу K2(x) > 0, которая удовлетворяет уравнению Риккати, коэффициенты которого зависят от x. Уравнение (17) решается многократно при фиксированном x ∈ Rn. Координаты вектора состояния определяются в процессе интегрирования дифференциального уравнения (12) совместно с управлениями объектом и возмущениями:

u *( x ) = - Q ^{, - 1} ( x ) B T ( x ) K ₂ ( x ) x , w *( x ) = -^-P' ^{- 1} ( x ) B T ( x ) K ₂ ( x ) x .                            (18)

Y

При этом решение уравнения Риккати должно быть таким, чтобы удовлетворялся критерий o{A(x) + [B1 (x)P,-1 (x)BT (x) - B2 (x)Q 1-1 (x)B2T (x)]K2 (x)} c CVx £ Rn, где о — спектр матрицы, C — открытая Y левая полуплоскость комплексной плоскости. Заметим, что критерий устойчивости замкнутой системы можно заменить проверкой поточечного выполнения критерия Рауса-Гурвица.

Алгоритм приближенного синтеза Н ∞ – регуляторов по состоянию

Шаг 1. Задать параметр γ > 0.

Шаг 2. Найти решение уравнения

x( t) = A (x (t)) x (t) + B1 (x (t)) w (t) + B 2 (x (t)) u (t), x (0) = 0, с управлениями u (t) = u * (x (t)) = - Q-1 (x (t)) B 2 T (x (t)) K 2 (x (t)) x (t), w (t) = w *( x (t)) = 2-P(x (t)) Bi (x (t)) K 2 (x (t)) x (t),

Y одним из численных методов интегрирования с постоянным шагом h (явным методом Эйлера, методом Эйлера–Коши, методами Адамса–Бэшфорта, Милна, Хэмминга различных порядков).

При этом для каждого из дискретных моментов времени t i = ih , i = 0, 1, 2, … решить уравнение Риккати:

K 2 (x) A (x) + AT (x) K 2 (x) - K 2 (x) [ B2 (x) Q ’* (x) B2 T (x) - -12- B1 (x) P ^‘ (x) B1T (x)] K 2 (x) + CT (x) S (x) C (x) = O, Y при x = x(ti ). В результате найти матрицу K2(x) и использовать ее при формировании законов управления.

Шаг 3. Найти минимальное γ*. Для этого требуется последовательно уменьшать γ пока свойство устойчивости решений дифференциального уравнения

x ( t ) = [ A ( x ( t )) + ^ B 1 ( x ( t )) P -1 ( x ( t )) B? ( x ( t )) - B 2 ( x ( t )) Q -¹ ( x ( t )) B 2 ^T ( x ( t ))] K 2 ( x ( t )) x ( t ) ,

Y описывающего динамику системы с полученными управлениями, остается справедливым.

Результаты исследования. Для проверки эффективности предложенного приближенного алгоритма синтеза Н ∞ – регуляторов по состоянию решены два модельных примера.

Модельный пример №1. Рассмотрен одномерный случай, когда уравнения (1), (2) и функционал (5) имеют вид: x( t) = f (x) + B1 (x) w + B 2 (x) u = A (x) x + B1 (x) w+B 2 (x) u, y = C (x) x,

I = | [ S ( x ( t )) x ² ( t ) + Q ( x ( t )) u ² ( t ) - у ² P ( x ( t )) w ² ( t )] dt .

Решение. Структуры управления следуют из (18):

u *( x) = - 1— В 2(x) K 2(x) x, u *( x) = - 1— В 2(x) K2(x) x, Q(x)

а уравнение (17) имеет форму:

B,2 (x)       1       ,    ’,

2 A ( x ) K 2 ( x ) - K 2 ( x )

'„' ) -^— B 2 ( x ) + C ² ( x ) S ( x ) = 0.

Q (x)   у2 P (x)

Запишем полученное квадратное уравнение в канонической форме:

Решение имеет вид:

K 2 ( x ) =

B y x ) - ^-1— B l ( x ) K 22 ( x ) - 2 A ( x ) K 2 ( x ) - C ² ( x ) S ( x ) = 0.

L Q ( x ) Y ² P ( x )

4 A 2 ( x ) + 4 C 2 S ( x )	[ B ^ - ^ B ,2 ( x ) 1 _ Q ( x ) y 2 P ( x ) 1 V _

2 A ( x ) ±

2

[ B     -         B 2 ( x ) 1 _ Q ( x ) у 2 P ( x ) 1 V _

.

Поскольку K 2 > 0, то:

A ( x ) + A 2 ( x ) + C 2 S ( x ) [ B^x- -        B 2 ( x )

, 4          V                     Q ( x )    Y 2 P ( x ) 1

K ( x ) =

B ^ -       B. 2 ( x )

L Q ( x )    Y2 P ( x ) 1 V 7 J

Рассмотрим подробнее частный случай:

x(t ) = x - x ³ + w + u = (1 - x ²) x + w + u , У = 2 x ,

I = j [ x ² ( t ) + u ² ( t ) -Y ² w ² ( t )] dt , где A ( x ) = (1 – x ²), B 1 ( x ) = 1, B 2 ( x ) = 1, C ( x ) = 2⁰, Q ( x ) = 1, S ( x ) = 1, P ( x ) = 1.

Тогда (опуская зависимость от х ) получаем:

2 AK ₂ - K ₂ ² 1 1 -| + C ² = 0 ^ K ₂ ² ( 1 -у - ² ) - 2 AK ₂ - C ² = 0.

Корни квадратного уравнения

K 2 =

A ± 7 A ² + C ² (1 -Y - ² ) i-T ²

C ²

Y* 1, K 2 =^-    , Y = 1.

2 A

Информатика, вычислительная техника и управление

Заметим, что при рассмотрении случая γ ≠ 1 пока невозможно исключить лишние корни, так как A ( x ) и (1 – γ^–2)

могут изменять знак.

В результате получаем структуры управления:

w *( x ) = -2 B 1 TK ₂ x = —2 K ₂ x , u *( x ) = B ₂ TK ₂ x = - K ₂ x .

Y           Y

При этом уравнение замкнутой системы имеет вид:

x = [ A - (1 - y^{- 2} ) K ₂ ] x = + 7 A ² + C ² (1 -y^{- 2} ) x .

Для обеспечения асимптотической устойчивости берем знак минус, а в выражении для K 2 — плюс. Для дан-

ного примера получаем: 1) если γ ≠ 1, то

A ( x ) + 7 A ² ( x ) + C ² ( x )(1 -y^{- 2} ) 1 - x ² + 7 (1 - x ² )² + 4(1 -Y - ² ) 1 -y^{- 2}             =             1 -Y^{- 2}

> 0.

2) если функции A ( x ), C ( x ) не равны нулю одновременно, то дискриминант A ²( x ) + C ² ( x )( 1 – γ^–2). Тогда

A ² ( x) + C ² ( x) >  C ² ( x ) y^{- 2} ,

- 2 <  A ² ( x ) + C ² ( x )

^Y          C ² ( x )

2 >      C ² ( x )        2 ₍₎ =      C ² ( x )

^Y “A ² ( x ) + C ² ( x ), ^YmmW A ² ( x ) + C ² ( x ).

Для решаемого примера y min ( x ) =

C ² ( x )     =      4

A ² ( x ) + C ² ( x ) = (1 - x ² )² + 4,

т.е. при каждом текущем x имеется свое зна-

чение γ² ( x ).

min

При γ = γ min выполняется x = 0, x (0) = 0 (условие асимптотической устойчивости не выполняется, но справедливо x ( t ) ≡ 0).

При γ = γ_m i _n имеем

A ( x ) + 7 A ² ( x ) + C ² ( x )(1 -y^{- 2} ) = 1 - x ² + 7 (1 - x ² )² + 4(1 -Y - ²) 1 -Y - ²                             1 -Y - ²

> 0,

Y * 1 .

C ² ( x )

Если y = 1, то K ( x ) =--

,       ²        2 A ( x )

—

. Для выполнения условия K 2 > 0 требуется выполнение условия 2(1 - x ²)

A ( x ) = 1 – x ²< 0 задающее множество | x | < 1 возможного функционирования системы.

Моделирование. Для моделирования при различных начальных условиях был выбран конечный промежуток времени T = [0, 20], поскольку все переходные процессы в замкнутой системе практически завершаются.

Согласно рис. 1–3, значение вектора состояния асимптотически стремится к нулю для различных начальных условий, что свидетельствует об устойчивости системы и правильном выборе параметров, при которых система сохраняет свойство устойчивости при любых заданных ограниченных возмущениях.

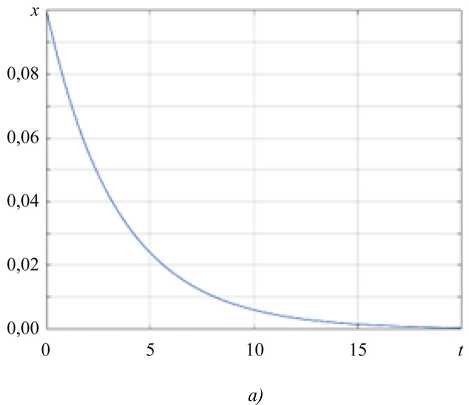
Рис. 1. Изменение вектора состояния: а — для начального состояния x 0 = 0,1; б — для начального состояния x 0 = –0,1

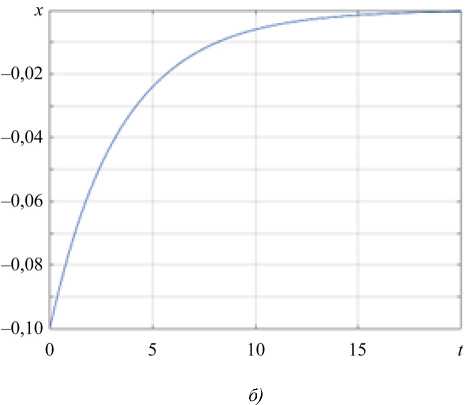
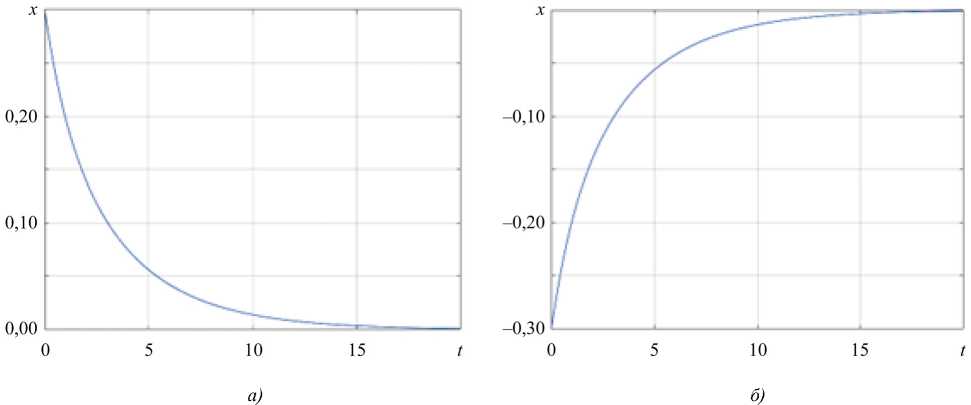
Рис. 2. Изменение вектора состояния: а — для начального состояния x 0 = 0,3; б — для начального состояния x 0 = –0,3

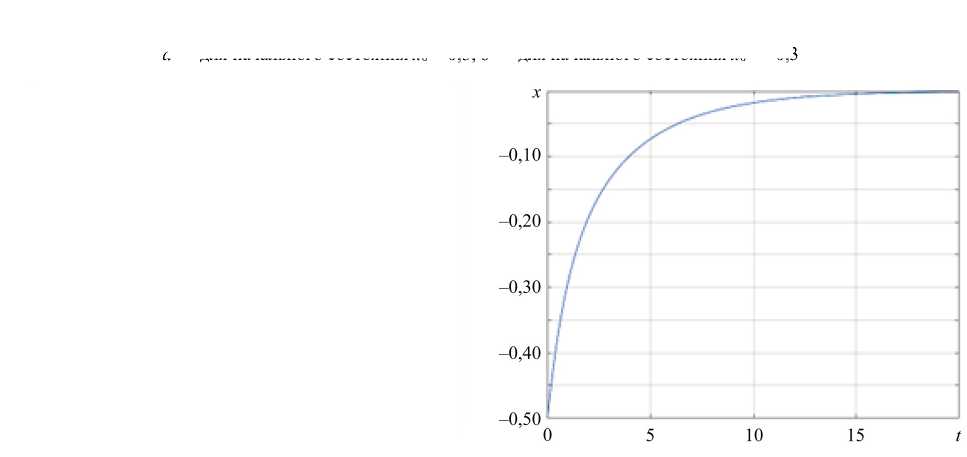
б)

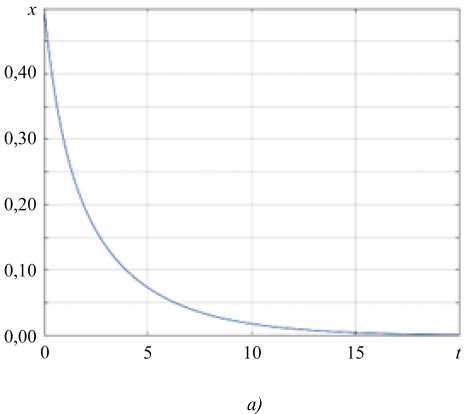
Рис. 3. Изменение вектора состояния: а — для начального состояния x 0 = 0,5; б — для начального состояния x 0 = –0,5

Модельный пример № 2. Рассмотрен один из вариантов двумерного случая, когда уравнения (1), (2) и функционал (5) имеют вид:

_ ( 0 x ( t ) = I

I ^x i '

^—^^ A ( x )

( 0 I _ I 1 I u ⁽ t ),

'—,—1

B 2 ( x )

1 I _ ( 0 I

0 I x ⁽ t) + I 1 I w ⁽ t ) + —                           .

B 1 ( x )

y ( t ) = x ( t),

®

I (u, w) = j [ xT (t) x (t) + u2 (t) - у 2 w2 (t)] dt < 0, т.е. C(x) = E2, S(x) = E2, Q(x) = 1, P(x) = 1.

Решение. Структуры управления объектом и возмущением следуют из (18):

K 11 ( x )

K ₁₂ ( x )

K 12 ( x ) |( x 1 |

II I = -K12 ( x) xi - K 22 ( x) x 2 , K 22 (x) Д x2 J w *( x) =

K 11 ( x )

K 12 ( x )

K ₁₂( x )

K 22 ( x )

Информатика, вычислительная техника и управление

и уравнение (17) имеет форму:

f K 11 ( x )   K 12 ( x ) Y 0  1 ^  ^ 0   x 1 V K 11 ( x )   K 12 ( x ) ^

t K 12 ( x )   K 22 ( x ) Д x 1   0 J\ 1  0 K 12 ( x )   K 22 ( x ) ^J-

• -f K ii ( x ) K 12 ( x ) W 0 Y      £ f 0 Y 0    V K ii ( x ) K 12 ( x ) W 1 0 V 0 0 ^

t K 12 ( x )   K 22 ( x ) Д 1/    ’  Y ² 1 1 /    1 K 12 ( x )   K 22 ( x ) ^J  ^ 0  1 J   [0   0 ^J .

Отсюда

2 K ₁₂ x ₁ -5 K 12 + 1 = 0,

K ₁₁ + K 22 x ₁ -5 K ₁₂ K 22 = 0,

2 K ₁₂ -5 K ₂ 2 ₂ + 1 = 0,

• Y ² - 1 где 5 = —2 = 1 -y 2 .

• Y ²

Решение первого уравнения δ K ₁²₂ - K ₁₂ x ₁ - 1 = 0 имеет вид:

2 x ₁ ± 4 x 2 + 45    x ₁ ± x 2 +5

K =--------------=

• 12          255

Решение третьего уравнения:

12 K ₁₂ + 1    2 x ₁ + 5± 2y/ x 2 +5

K 22 =           =         52

Решение второго уравнения:

2 x , + 5± 2 Jx 2 +5   /—г---

K_n = K ₂₂ (5 K ₁₂ - x ) = J            ----± x_x 2 +5 .

В полученных решениях выбраны положительные знаки с учетом условия K 2 > 0.

Моделирование. Для моделирования системы требуется подобрать такое минимально возможное значение γ, чтобы оно удовлетворяло (4) и в то же время гарантировало асимптотическую устойчивость замкнутой системы. В примере 1 аналитически была найдена величина параметра γ, но возникла проблема с определением значения оптимального параметра γ*, поэтому значение γ, используемое при моделировании, было выбрано экспериментально. При γ * = 1,5 сохраняется устойчивость системы согласно выражению (19). Для моделирования был выбран интервал времени T = [0, 10], так как переходные процессы в замкнутой системе затухают достаточно быстро. Моделирование проводилось для различных начальных условий.

Согласно рис. 4–5, можно сделать вывод, что координаты вектора состояния асимптотически стремятся к нулю. Данный результат наблюдается для каждого из рассмотренных начальных условий. Это свидетельствует о том, что система устойчива, а ее параметры подобраны корректно, что позволяет сохранять свойство устойчивости при любых начальных условиях и в условиях наихудших возмущений.

Начальные условия существенно влияют на траектории изменения координат вектора состояния, но из рис. 4–5 видно, что предложенный подход позволяет не только компенсировать внешние возмущения, но и стабилизировать траекторию движения.

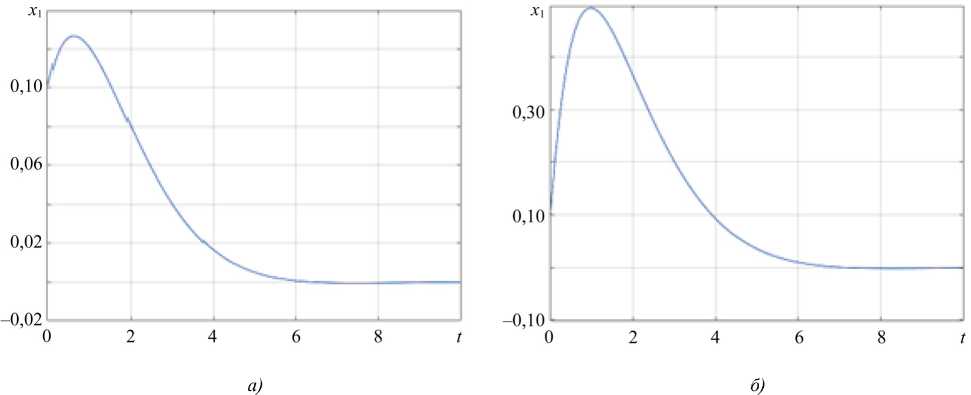
Рис. 4. Изменение x 1 ( t ): а — для начального состояния x 0 = (0,1; 0,1) ^T ; б — для начального состояния x 0 = (0,1; 1) ^T

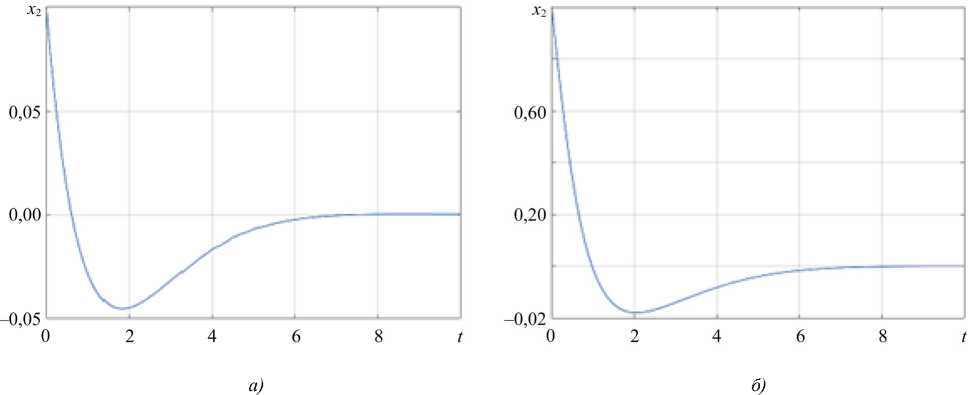
Рис. 5. Изменение x 2 ( t ):

а — для начального состояния x 0 = (1; 0,1) ^T ; б — для начального состояния x 0 = (1; 1) ^T

Обсуждение и заключение. В результате работы были сформулированы и обоснованы достаточные условия Н ∞ – управления, предложен приближенный метод решения. Предложенный в рамках задачи метод был проверен на двух модельных примерах. Результаты моделирования позволяют заключить, что использование разработанного метода синтеза регулятора гарантирует необходимое качество переходных процессов и обеспечивает асимптотическую устойчивость замкнутых систем.

Результаты и методы, предложенные в данной работе, могут быть применены для решения задач управления различной сложности — от проектирования простых автопилотов до разработки сложных систем автоматической навигации для пилотируемых и беспилотных летательных аппаратов. Это подчеркивает перспективность использования предложенного подхода и делает его привлекательным вариантом для дальнейших исследований.