Приближенный способ решения дифференциальных уравнений статики сыпучей среды

Как известно, решение дифференциальных уравнений теории предельного равновесия сыпучей среды с учетом объемных сил для двух семейств линий скольжения может быть получено лишь методом конечных разностей, за исключением частного случая, когда в рассматриваемой обла сти угол наклона главных площадок с осью координат постоянный.

Для того чтобы расширить использование теории предельного равновесия сыпучей среды в инженерной практике, в ряде исследований разрабатывались приближенные решения, основанные на неко

торых допущениях [1; 2], среди которых наиболее часто встречаются:

• 1)    пренебрежение объемными силами ввиду малости областей предельного равновесия;

• 2)    равенство нулю угла внутреннего трения;

• 3)    исключение из учета в инженерных расчетных схемах влияния объемных сил на очертание линий скольжения.

Следует отметить, что все допущения отвечают практической точности расчета, однако разработанные приемы могут быть привлечены и для решения частных задач.

В настоящей статье предлагается приближенный метод интегрирования дифференциальных уравнений линий скольжения для одного распространенного случая — для области радиальных сдвигов с учетом собственного веса (рис. 1).

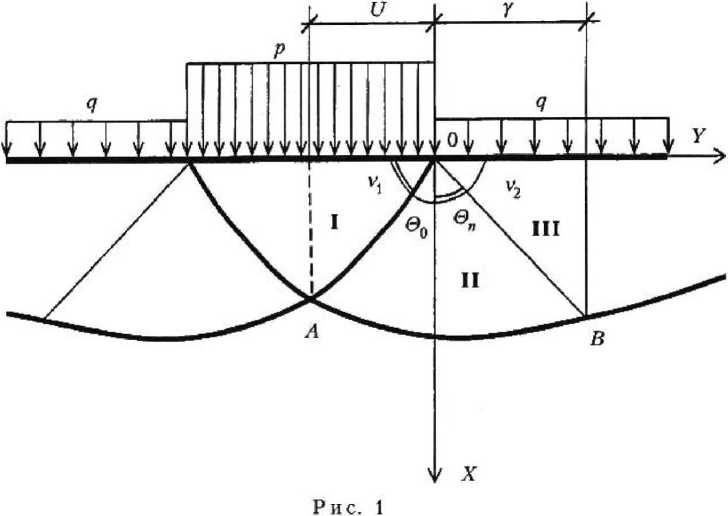
Были преобразованы исходные уравнения статики сыпучей среды, дифференциальные уравнения равновесия:

^+^+х = 0;

дх ду

• —^ - + ^ + У=0

Эх Эу и условие прочности грунта:

И (_       \2      2 _

V 4 ^ ^аУ^ * ^ТхУ ~

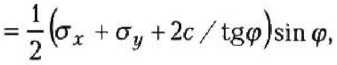
или

(сг1 - сг2) = (<т1 + сг2 + 2c/tg

Здесь сг_г, с^, т Ст], сг₂ — соответственно компоненты напряжений в точке на площадке, параллельной координатным осям, и главные напряжения (рис. 2).

о

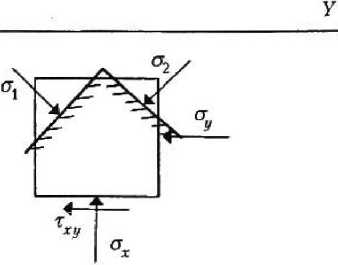
Р и с. 2

Для невесомой сыпучей среды уравнения первого семейства линий скольжения имеют вид r = raexp[(0„-0o)tg

o' = cr0 expfct^ - 0p)tg

si n ^9

AL = ■ А 6Х_Р[(0_Л ~ ⁰O Xg

X

7 Sin 0g        ”

где <7, (7g — средние фиктивные напряжения соответственно в произвольной точке линий скольжения и в точке А.

Второе семейство линий скольжения представлено радиальными линиями.

Для интегрирования разбили линию скольжения АВ на п участков (рис. 3). Для каждого участка значение Д (А = = Х_х + Y_y) принято постоянным. Полученные после интегрирования результаты были использованы для определения коэффициентов формулы предельного давления на грунтовое основание по подошве жесткого фундамента:

tg 7“вп

l + sin^cos2jg

1 - sin ф exp [2(0_О - 9_n )tg

_ exp[-2 (©„ - 0O )tg

7Г

A cos ф cos 6*q + —-

exp[2(0o-0„)tg

x [exp (30„ tgp) sin(

O_n - e) + + exp (3 0g tg^) sin(£ + 0g - y)j -

71 1

- tg 0Q + — I

P = N_vY-N_qq-N_cc, (5)

1+sin (р cos 2/3

где у q c

• —    удельный вес грунта;

• —    боковая пригрузка;

— удельное сцепление грунта.

(l-sin(p)exp[2(0_o - 0„Уйф\

■ (7)

1 + sin (p cos 2/3

(1 - sin

O -

0_n )tg tp]

_ 1 tgp

Здесь

-и

It

— — V

2 ’

M^ = v.

"U * 1

. f 1

e - arcsin —

Рис. 3