Приближённый анализ электродинамических процессов распространения сигналов по двухпроводной симметричной линии

Вопросы применимости различных приближённых методов анализа электромагнитных полей для модельной оценки интегральных параметров электро- и радиотехнических устройств всегда являлись и продолжают оставаться актуальными при совершенствовании их конструктивных исполнений и повышении требований к их эксплуатационным характеристикам.

Двухпроводные симметричные линии специальной конструкции часто используются в качестве соединителей между дистанционно-удалёнными высокочастотными блоками, в частности для различных технологических модификаций цифровых абонентских линий, которые ориентированы, прежде всего, на широкополосный доступ в Интернет при гарантированном качестве обслуживания с вероятностью возникновения ошибок в процессе передачи данных не более 10–7. Для эффективного решения проблем «последней мили» обычно используют симметричные высокочастотные кабели и витые пары различных категорий. Близкое расположение проводников кругового сечения частично обеспечивает определённую помехозащищённость от внешних и взаимных влияний в линии связи. Вместе с тем именно эта особенность создаёт дополнительное перераспределение плотности тока по сечению пары проводников, обусловленное эффектом близости. В итоге вытеснение тока к поверхности проводников при повышенных частотах и его дополнительное перераспределение вследствие эффекта близости приводят к увеличению вносимого затухания, что ведёт к ограничению полосы частот пропускания и к снижению максимально допустимой при заданном качестве обслуживания длины линии связи даже при идеальных прочих условиях. Применительно к реализации VDSL1-технологии, тоже относящейся к развивающимся цифровым технологиям информационного обмена (полоса частот от 1 МГц до 10 МГц, скорость передачи данных до 20 Мбит/с при длине линии от 1,2 до 1,4 км), влияние вышеуказанных следствий становится ещё более существенным. Обычные проектные оценки характеристик таких линий базируются или на аппроксимациях общетеоретических решений определённых модельных задач, или на методике эмпирически установленных соотношений и поправочных коэффициентов [1, 2].

В условиях сильно выраженного поверхностного эффекта и при достаточно малом расстоянии между проводящими поверхностями по сравнению с длиной электромагнитной волны становится возможным использовать промежуточный анализ распределения квазистационар- ного электрического поля, который в сочетании с принципом пропорциональности электрических и магнитных составляющих поля позволяет получать приближённые решения ряда электродинамических задач. Эти возможности исследовались ещё в 60-е годы прошлого века проф. К.М. Поливановым, но тогда ещё не могли быть распространены на более широкий класс прикладных задач. Более поздние результаты прикладных исследований [3] лишь частично использовали эту возможность путём обращения к методам зеркальных изображений в анализе электродинамических процессов СВЧ-диапазона. Применительно к приближённому анализу электродинамических процессов в двухпроводной симметричной линии и упрощённого определения её характеристических параметров за отправную точку исследования принимается промежуточное решение задачи о квазистационарном распределении электрического поля на проводящих поверхностях с последующим переходом к граничным условиям Леонтовича2.

Анализ модели двухпроводной линии

Конструктивные особенности двухпроводных симметричных высокочастотных линий определены их функциональным назначением. Если для обеспечения широкополосного доступа к различным локальным и ведомственным телекоммуникационным сетям на основе DSL-технологий необходимо достаточно малое затухание цифровых сигналов, что достигается, например, применением однопарного кабеля КАЦП-2×0,9, схематически представленного в его сечении на рис. 1, то для межстоечного монтажного соединения станционным кабелем КМС-1 допускается на порядок большее затухание вследствие ограниченной длины двухпроводной симметричной пары.

Конструктивные различия по диаметрам токопроводящих жил симметричных пар, используемых в телекоммуникационных сетях, заключаются в их значениях 0,9, 1,0, 1,1 и 1,2 мм, а для симметричной пары соединительной линии высокочастотных блоков это значение значительно меньше; например, для кабеля КМС-1 оно составляет только 0,6 мм. Наличие определённой экранирующей поверхности является общей характерной чертой двухпроводных высокочастотных симметричных линий, в качестве обобщённой модели которых принимается

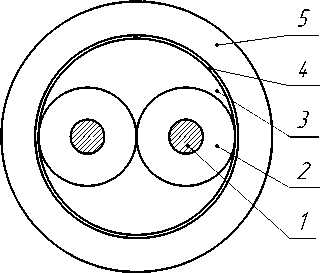
Рис. 1. Однопарный кабель в сечении: 1 – медная токопроводящая жила; 2 – изоляция жилы; 3 – сердечник из диэлектрического материала; 4 – экранирующая алюмополимерная лента; 5 – защитное покрытие геометрия системы проводящих поверхностей (рис. 1) при её различных конструктивных параметрах, что для неэкранированной симметричной пары может быть выражено отношением расстояния между центрами токопроводящих жил к их радиусу.

Согласно граничным условиям Леонтовича комплексное значение осевой составляющей E_z ( r 1 ) электрического поля на поверхности проводника радиуса r 1 в условиях сильно выраженного поверхностного эффекта должно следовать приближённому соотношению

Ez (rl ) = ZcHt X n, где Zc – волновое сопротивление материала проводника; Ht – комплексное значение тангенциальной составляющей магнитного поля на поверхности проводника; n – внутренняя нормаль к проводящей поверхности; (Zc = 4j^Цо К, j = V-Г, ю — угловая частота приложенного поля, γ – удельная электропроводность проводника, μ0 = 4π∙10–7 Гн/м).

Электромагнитное состояние на поверхностях токопроводящих жил (рис. 1) в смежных точках M , M ʹ, принадлежащих этим поверхностям, и соответствующее соотношению (1), показано на рис. 2.

При сильно выраженном поверхностном эффекте степень неравномерности распределения плотности тока 8 _z = ( r , а ) = y E_z ( r ,а ) , 0 <  r < r 1 характеризуют условной глубиной проникновения электромагнитного поля, интенсивность составляющих которого аппроксимируют экспоненциальным уменьшением от поверхности раздела сред «диэлектрик-проводник». Однако это приемлемо только в модели плоской электромагнитной волны, проникающей в проводящую поверхность при условии, что наименьший линейный размер условно плоского участка этой поверхности существенно превышает глубину проникновения поля. Для поверхности токопроводящих жил (рис. 2) аналогичная оценка степени неравномерности распределения плотности тока и применимости граничных условий Леонтовича требует дополнительного количественного уточнения, в частности, на основе уравнения электромагнитного состояния уединённого цилиндрического проводника, которое в комплексной форме представления имеет вид

d2δ1 dδ

2-+Т + — "jz — j ®YH о 5z = 0.

dr r dr

Введением новой независимой переменной Z = r4 ^W YH 0 ' V— 7 (° = 2п f) уравнение (2) сводится к уравнению Бесселя

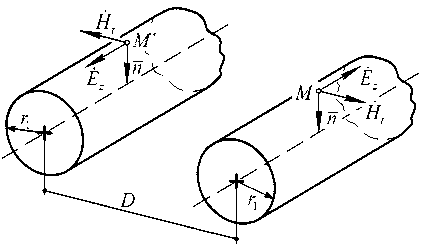
Рис. 2. Электромагнитное состояние на поверхностях токопроводящих жил

d2δ1 dδ

—f+-•  z- + 3. = 0,

dζ2   ζdζz решением которого является

M Z ) = 8 г ( 0) Jо (Z ),                                                        (4)

где о _z ( 0 ) - комплексное значение плотности тока на оси проводника (г = 0); J ₀(Z) - функция Бесселя нулевого порядка комплексного аргумента ζ.

Значение параметра r ₁ ωγμ₀ для медного (γ = 0,562 · 10⁸ См/м) цилиндрического проводника диаметром 1 мм даже при частоте f = 1 МГц равно 10,5, что уже относится к большим значениям модуля аргумента в решении (4), и для вычисления комплекснозначной функции J 0 (ζ) можно использовать асимптотику

J0 (Z) ”J 2 [ Ро (Z) cosфо (Z)-Qo (z) sin Фо (Z )],

где

P(H = 1__9   .  •     = -1+^^2^+  -Ф (Z) = Z+n

P 0 ^{( Z})   ¹    _n,/_o^\2 +•• ’;   Q 0 ^{( Z})          ⁺        x3 +•• •;  ^ф 0 ^{( Z})   ^{Z +}    .

2!( 8 Z)                    8 Z 3!(8Z)                     4

Результаты расчёта изменения отношения модулей δ _z δ ₀ плотностей тока в приповерхностных слоях медного цилиндрического проводника диаметром 1 мм, выполненные по зависимостям (4), (5), представлены на рис. 3.

Выполняя экспоненциальную аппроксимацию начального участка зависимости δ _z δ ₀ находим значение эквивалентной глубины ( r 1 – r e ) проникновения поля, равное 0,072 мм, которое в 7 раз меньше радиуса r 1 проводника. Таким образом, применимость граничных условиях Леонтовича при вышеуказанных условиях обоснована.

Обращаясь к классической модельной системе с круговыми сечениями токопроводящих жил однопарного кабеля как открытой двухпроводной симметричной линии (влияние экра-

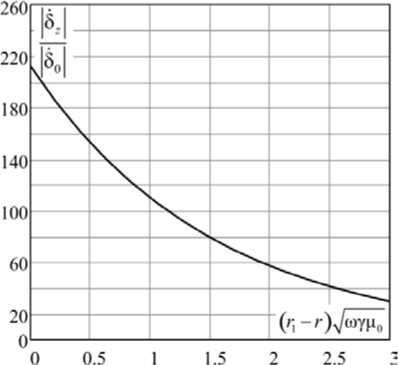
Рис. 3. Изменение отношения модулей плотностей тока в приповерхностных слоях медного цилиндрического проводника диаметром 1 мм при частоте 1 МГц

нирующей поверхности целесообразно учесть отдельно), заметим, что распределённая поверхностная плотность электрических зарядов может при этом эквивалентно заменяться фиктивными сосредоточенными линейными зарядами ±τ так, что эквипотенциальность круговых контуров сечения проводников сохраняется, если расстояние a между указанными фиктивными линейными зарядами относительно центра модельной системы определяется из соотношения

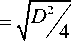
— r12

,

где D – расстояние между центрами токопроводящих жил; r ₁ – радиусы контуров сечений.

Распределение напряжённости электрического поля на контуре сечения проводника вычислим как радиальную составляющую градиента потенциала φ _М произвольной точки М , принадлежащей вспомогательному круговому контуру радиуса ( r 1 + Δ r ), согласно расчётной схеме (рис. 4) по соотношению

E r ( r 1 , ^a ) =

τ

2 π ε ₀ ε ₁

d φ M

• —---- d(Д r)

.

Д r ^ 0

Функцию φ _М находим суперпозицией потенциалов, создаваемых фиктивными линейными зарядами ±τ, в виде

Ф m =

τ 2πε0ε1

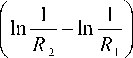
τ

2π ε0ε1

R

ln 1

R 2

где ε 1 – относительная диэлектрическая проницаемость среды, заполняющей пространство между проводящими поверхностями; ε₀ = 8.8542∙10^–12 Ф/м; а R ₁ и R ₂ – расстояния, определяемые, согласно геометрии расчётной схемы рис. 4, соотношениями

R

= {[( D/ 2 + a) + (r + Ar)

cosa ]2

+ (r + A r )2 sin2 a

Г

(D/2 + a) +(D + 2a)(r + Ar)cosa + (r1 + Ar) I :

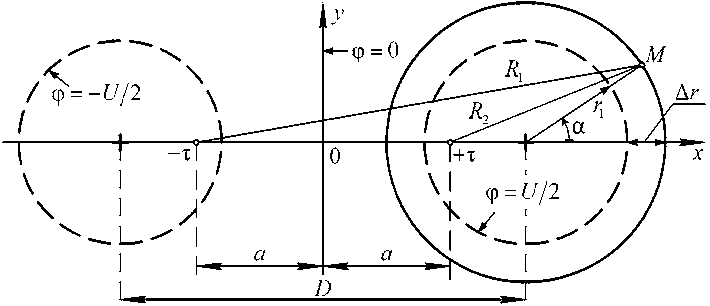
Рис. 4. Расчётная схема для вычисления распределения напряжённости электрического поля на поверхности проводника двухпроводной симметричной линии

2               2           ¹²

R 2 |[ ( DI 2 - a ) + ( r 1 + A r ) cosa ] + ( r + A r ) sin 2 a } =

= l(D/2 — a) +(D — 2a)(r + Ar)cosa +(r+ Ar) I .

Выполняя дифференцирование по соотношению (7) с учётом зависимостей (8), (9), (10) и учитывая при преобразованиях, слагаемых соотношение (6), получим искомое распределение напряжённости электрического поля на поверхности проводника в виде

Er (r1, a ) =

τ

— π ε0ε1r1

a

,

D + 2 r cos a

которое позволяет определить функциональные зависимости относительного перераспределения поверхностной плотности электрического заряда двухпроводной симметричной линии в виде

— = ^,D ² r )  -,

O U    D / ² Г + ^cosa

где о = о (r,a) = EoE,Er (r,a), aU = T/(2n r-).

Некоторые числовые значения, определённые по соотношению (12), показаны на рис. 5.

В процессе распространения сигналов по двухпроводной линии мгновенное электромагнитное состояние для фиксированного момента времени в поперечном сечении линии характеризуется распределением мгновенных значений ( E , H )-векторов соответственно напряжённостей электрического и магнитного поля. Для произвольной точки М , принадлежащей плоскости сечения пространства между проводящими поверхностями, которая совмещена с комплексной ( x , jy )-плоскостью, ( E , H )-векторы показаны на рис. 6. Значение потока электрического поля через криволинейный параллелепипед единичной длины ( l = 1) в направлении

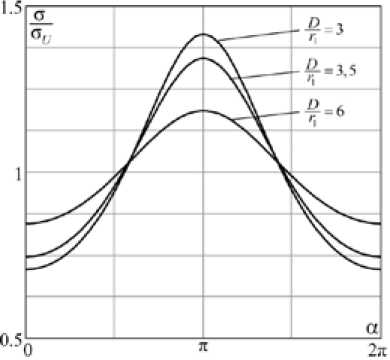
Рис. 5. Зависимости относительного перераспределения поверхностной плотности электрических зарядов на проводниках симметричной двухпроводной линии

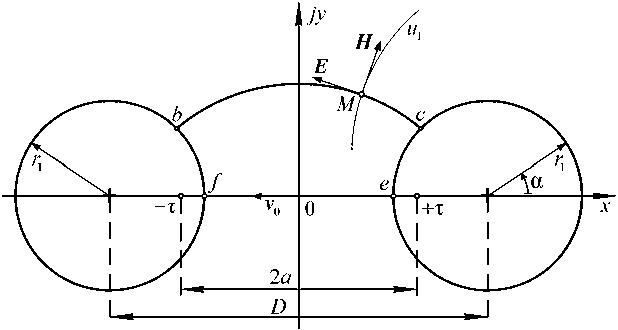
Рис. 6. Плоскость сечения двухпроводной симметричной линии, совмещённая с ( x , jy )-плоскостью

осевой координаты, перпендикулярной сечению, ограниченного двумя линиями v , v потока поля ( v = const ) и двумя эквипотенциалями ( u = const ), определено мгновенной поверхностной плотностью электрического заряда σ( r ₁, α) соотношением

J о (rva) rd а = S0S1 fc (гиа). d а = ( v - vo) EoEl, (13) αcαc где Er(r1, α) – функциональная зависимость (11).

Значения ( E , H )-векторов электромагнитного поля могут быть выражены через градиенты скалярных функций u ( x , y ) и v ( x , y ) по зависимостям

E =- c , V и ( x ^, y ) ; H =- c 2 V v ( , ^, y ) ^, (14) где V - оператор набла ( V = e _x 8/8 x + e _y 8,8 y ); ( c 1 , c ₂) - размерные коэффициенты пропорциональности.

Модули градиентов в (14) зависят от ( x , y )-координат точки М , но имеют равные значения, т.е. V и ( x , у ) = V v ( x , y ) , что следует из условий Коши-Римана конформных преобразований. Пусть точка М перемещена на поверхность проводника, тогда значение v v зависит только от одной угловой переменной, т.е.

1 д v

^V v = e a--7-= e a r i 8 a

1a -----------•------------------------------------------- nri D + 2ricosa

Из соотношения (15) следует, что V v представляет собой нормированное распределение напряжённости магнитного поля на поверхности проводника. Действительно, выполняя интегрирование по контуру кругового сечения проводника, получаем

2π2aπdα

I V v r1 da =--I-------------0           n 0D+2ricosa

4an JD2 - 4 r2

arctg

(D - 2 ri) tg a/2

Do^8

π

=1, (16)

т.е. получаем тождество, которое справедливо при любых D > 2r1 и условии симметрии углово- го распределения мгновенного поверхностного электрического заряда.

Известно, что циркуляция напряжённости H магнитного поля на контуре, охватывающем токи, в данном контексте на контуре кругового сечения проводника с током i , численно равна его значению, т.е. имеет место соотношение

2π

J H_t ( r 1 , a ) r 1 d a = i ,                                                                (17)

из которого следует, что умножение тождества (16) на комплексное значение тока I , при условии симметрии углового распределения плотностей тока в сечении проводника 5 z ( r 1 ,a ) , (0 ≤ r ≤ r 1 ), позволяет найти угловое распределение тангенциальной напряжённости H t магнитного поля на поверхности токопроводящей жилы двухпроводной симметричной линии в виде

H t = “ ■ n/ a ----.                                      (18)

^п r 1 D + 2 r cos^a

Возвращаясь к приближённым граничным условиям (1), определим часть электромагнитной энергии Δ P в единицу времени, проникающей через проводящую поверхность единичной длины жилы, с учётом зависимости (18):

_дP = -Refr E xH* 1 ds = -Re

2 J L z ^- J 2

222 π

'J Zn  rr'a   V n ri   " (D + 2 r-cos a)

I ² D ωμ 0 8π r ₁ a   2γ ,

= Re

4 to 2 d"   V n r- b (D + 2 г-cos a)

где учтено, что Re [ z _c ] = ^®ц ₀ /( 2y ) , а в результате интегрирования получено

D ^π d α

⁺ D² - 4 r i ^{2 J} D + 2 r i cos^a

D 2ππ D

D = -⁴ r- D^ ² - ⁸ a>

(______ d =₇_______ 2 r L^ina________

о ⁽ D + ² r - cos ^a ) ⁽ 4 ^r - D ^{2)( a} + ² r - ^cosa )

D         2          ( D - 2 r ) tg a/2

= nr:i;2 ' /;.2 _л 2 ^arctg    /^2/2

D  ⁴ r 1   V D ^{- 4} r i         4D ^{- 4} r i

Поскольку суммарные электромагнитные потери мощности на единицу длины двухпроводной симметричной линии равны удвоенному значению, определённому зависимостью (19), то активное сопротивление ^1 (r1) на единицу длины для рассматриваемой модельной системы равно

^ ( r ) = -D - J®^^ .

¹¹   4π r 1 a 2γ

По зависимости (19) находится и часть реактивной энергии Δ Q как мнимая часть потока электромагнитного поля, проникающая в токопроводящую жилу, равная

A Q = - Im Г" E-х H t 1 ds =---- Im [ z_c ] ,

2s                 8π r1a которая позволяет найти индуктивность L1(int) на единицу длины линии, обусловленную внутренним электромагнитным полем, равную

_L  Δ Q D μ 0

^{1 (} int )   го 1 ² 4n r 1 a у 2ю у

Приближённый расчёт влияния экранирующей поверхности однопарного кабеля на его первичные параметры тоже может основываться на предварительном анализе квазистацио-нарного распределения поверхностной плотности ε 0 ε 1 E n электрических зарядов, индуцируемой полем знакопеременных электрических зарядов жил кабеля, на цилиндрической поверхности экрана радиуса r 0 . На рис. 7 показана расчётная схема, в которой путём введения согласно методу зеркальных изображений [3], инверсных относительно цилиндрической поверхности экрана дополнительных линейных зарядов ±τ, но при этом эквипотенциальность контуров токопроводящих жил сохраняется здесь только в окрестностях точек 1, 2 неограниченной расчётной среды с относительной диэлектрической проницаемостью ε 1 .

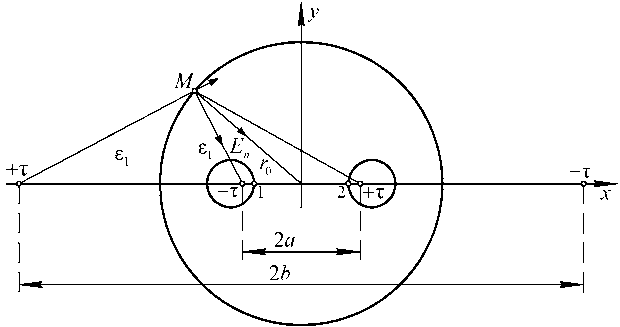
Рис. 7. Расчётная схема учёта влияния экрана однопарного кабеля на его первичные линейные параметры

Разность потенциалов между точками 1, 2, принадлежащими контурам радиуса r 1 , определим в системе четырёх линейных электрических зарядов суперпозицией функций логарифмического потенциала соотношением

τ

Ф 2 ^— Ф 1 =-----

π ε 0 ε 1

( ln -

a + D ² — r i ) _— ln ( b ⁺ D ² — r ) . ^{a —} D 2 + ^ri )    ( b ^— D 2 + r i ) _

—

;

b ^— ra ’ [ - D ² ) 2 ^— r i² Г< a <  a 0 - r o ) , ⁽²³⁾

из которого следует, что ёмкость на единицу длины двухпроводной симметричной экранированной линии

τ

Ci —       — K£ 08i ф1— ф2

1)"

1² — 1 + D 2 r l )    ( x7( D 2 , Г — I + D 2 r —

^—     2     " (X ^ D ^1)‘—' - D 2 Г + 1 ) J

— 1

, (24)

На рис. 8 показана зависимость ёмкости C 1 для некоторых значений переменной D / r 1 при ε 1 = 2.

Как следует из выражения (24), с увеличением значений параметра экранирования χ более 8 ёмкость C 1 стремится к её значениям для неэкранированной симметричной пары, представленным на рис. 8 а . При типичных конструктивных параметрах ( r 1 = 0,5 мм; r 0 = 3 мм; D /2 =1,5 мм) увеличение ёмкости C 1 , обусловленное круговой экранирующей поверхностью, не превосходит 15 % от соответствующего значения C 1 неэкранированной симметричной пары, что уже нужно учитывать при вычислении волнового сопротивления и характеристических параметров двухпроводной экранированной симметричной линии.

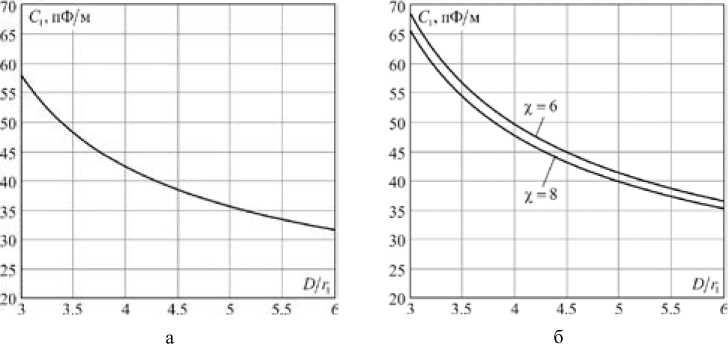
Рис. 8. Зависимость ёмкости C 1 симметричной пары на единицу длины для некоторых значений переменной D / r 1 : а – неэкранированная симметричная пара; б – экранированная симметричная пара

Таким образом, на основе приближённого анализа модельной системы двухпроводной высокочастотной симметричной линии могут быть приняты в качестве её продольных параметров

K,^.D,,r,ю);    L.(D,r )= L„. a+L     L., A,(25)

1      1        1’7’          1        1        1( int) 1( ext) 1( ext)’ где L1  – внешняя индуктивность токопроводящих жил на единицу длины линии без учёта

( ext )

внутреннего магнитного поля в приповерхностном слое проводников –

L, ,, Ho In 1'“l П

Соответственно, в качестве поперечных параметров примем линии

C1=C, (D, r„ X);     G1=G1 (D, r ,x),    X = r02 /a2,

где активная составляющая G1 поперечной комплексной проводимости линии на единицу длины определена двумя слагаемыми, первое из которых пропорционально угловой частоте ω и – 553 – тангенсу угла tgδ диэлектрических потерь в среде, прилегающей к токопроводящим жилам, а второе – электромагнитными потерями на проводящей поверхности экрана –

G i = ® ^C 1 ( 1 ) tg ⁵ = ® ^п£ o ^£ i

и ² a + D - ² r i

2 a - D + 2 r

-J

• tg5

,

X =^

,     ^P ( r)

i2 )      U -

Зависимости (25), (26) позволяют приближённо вычислять характеристические параметры линии как частотнозависимые составляющие комплексного коэффициента распространения n (- )+je (*)-[(*i + j- L)( G+j^f, где η(ω), β(ω) – коэффициент затухания и коэффициент фазы соответственно.

Преобразованием правой части соотношение (27) привод2им к виду

n(to) +jв(to) = jto jlCcx [1 + ^/(jtoLi )J -[1 + Gi /(jtoCi )J , в котором при достаточно высокой частоте выполняются условия toLi 5> ^1, toC 1 3> Gi так, что функции-сомножители в скобках могут быть представлены их разложениями в ряды, т.е. приближённо получаем зависимости

[1 + ^i/(jto Li ^ 1 + ^i/(2 j to Li);   [1 + G/(j toC,)    1 + G] (2 j toC,),

M jL).GK2j.C . ) , как более

которые в их произведении позволяют опустить слагаемое высокого порядка малости и переписать (27) в виде

n ⁽ «W ( « )- «i/ ( ² Z .) ₊ GZ w /2 . j « C ,

где z w – волновое сопротивление двухпроводной линии, которое при достаточно высоких частотах с учётом зависимости (24) и отсутствия экрана определено в виде

L i ГЙТ Г. D - r , 2 a + D - 2 r —      2-°-• In----- ^L- In------------ ^L

(3 )

y ^{C i n}y^e ° ^{£ i} L r      ² a ^{D + 2} r.

Приравнивая в соотношении (30) вещественные и мнимые части, получаем характеристи- ческие параметры двухпроводной симметричной линии n (to) = «i/( 2 Zw ) + GiZw/2;                                              (32)

^{e (} to ) = to^ ^L i ^C i -

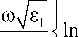
и - i

2 a + D — 2 r ln

2 a — D + 2 r

D—r

r

где c - x/yj £ o ц o - ³-to ⁸ м/с .

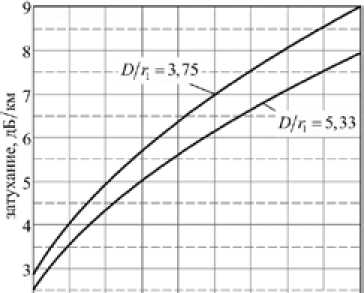
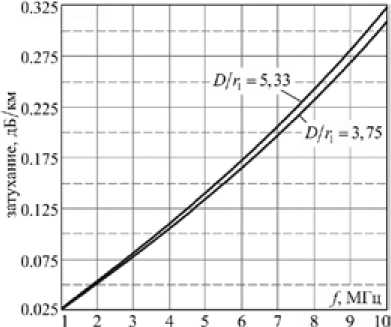
На рис. 9 показаны численные значения составляющих затухания на единицу длины ли- нии по зависимости (32) при некоторых значениях D/r .

Первое слагаемое в (32) вычислялось для параметра D/r = 5,33 при D/2 = 1,6 мм и r = 0,6 мм, а для параметра D/r = 3,75 при D/2 = 1,5 мм и r = 0,8 мм. Изоляция токопроводящих жил принималась полиэтиленовой с tgδ = 2,2 · 10–4 при f = 1 МГц и tgδ = 2,7 · 10–4 при f = 10 МГц. Ре- зультаты (рис. 9б) получены без учёта слагаемого G (2), дополнительное вычисление которого показывает, что для типовых конструктивных исполнений выполняется условие G G 2

– 554 –

|             /МШ|

1   2   3   4   5   6   7   8   9 10

б

Рис. 9. Составляющие затухания на единицу длины двухпроводной симметричной линии: а – составляющая затухания, вносимая токопроводящими жилами; б – составляющая затухания, вносимая диэлектрической средой, прилегающей к поверхностям токопроводящих жил

а

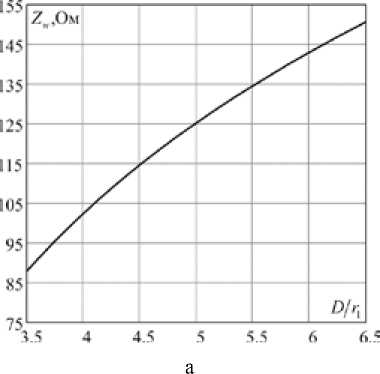
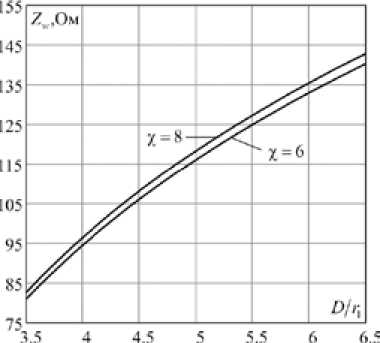
Рис. 10. Зависимости волнового сопротивления симметричной двухпроводной линии для некоторых значений : а – неэкранированная; б – экранированная

б

и учёт электромагнитных потерь на экранирующей оболочке двухпроводных симметричных линий может являться предметом теоретического анализа. Сравнение результатов на рис. 9 также демонстрирует, что вносимое затухание диэлектрической средой, прилегающей к поверхностям жил двухпроводной симметричной линии, составляет только несколько процентов от затухания, вносимого проводящими поверхностями, которое быстро возрастает при уменьшении значений D / r 1 .

На рис. 10 показаны расчётные зависимости волнового сопротивления z_w для некоторых значений D / r 1 при ε = 2.

Значения волнового сопротивления Z_w (рис. 10) вычислялись без учёта внутреннего электромагнитного поля токопроводящих жил. Для уточнений значений L 1 используем соотношение (25) и зависимость (22) в виде

L = L_x, J1 + L_x( JL_X( J = L_x, K² Dk , и),                       (34)

1         1 ( ext ) l 1 ( int )/      1 ( ext ) |          1 ( ext )                  1’

где K2 (Dr, го) = 1 + D (4 г a Цо) • [In (Dlri - 1)] 1- ^/ Цо/(2toY).

Уточнение значений Z w в (31) может сводиться к их умножению на коэффициенты K ²( D / r , ω), которые при f = 1 МГц для D / r ₁ = 3,75 и D / r ₁ = 6 соответственно равны 1,012 и 1,011.

Заключение

На основе анализа модели двухпроводной симметричной высокочастотной линии получены приближённые аналитические зависимости, которые позволяют относительно просто учитывать эффекты электромагнитного влияния близкого расположения токопроводящих жил и вытеснения тока к их поверхности. Современное разнообразие конструктивных особенностей симметричных пар и электрофизических свойств используемых материалов в сочетании с тенденциями повышения скорости передачи цифровых сигналов и пропускной способности каналов передачи данных являются факторами, при которых необходимость в проектных оценках характеристических параметров двухпроводных симметричных высокочастотных соединительных линий возрастает. Ограничения области применимости полученных аналитических результатов могут уточняться вычислительным моделированием соответствующих электромагнитных полей, что потребует бóльших временных и материальных ресурсов.