Приемник сигналов с минимальной частотной модуляцией

ПРИЕМНИК СИГНАЛОВ С МИНИМАЛЬНОЙ ЧАСТОТНОЙ МОДУЛЯЦИЕЙ

Рассмотрены последовательная и параллельная схемы приемника сигналов с минимальной частотной модуляцией на основе оптимальных методов. Исследованы погрешности устройства при измерении амплитуды и фазового сдвига.

Сигналы с минимальной частотной модуляцией (МЧМ) представляются в виде суммы двух ортогональных фазоманипулированных (ФМ) сигналов, сдвинутых на длительность посылки T и выраженных формулами

S ( t ) - I ( t )cos( w₀t + ф) - g ( t )sin( w₀t + ф), I ( t ) -C ( t )|cos( t n/2 T )|, Q( t )=S( t )|sin(tn/ 2 T)|, где I ( t ) и Q(t) - комплексные огибающие квадратурных компонент МЧМ сигнала; C ( t ) и S ( t ) - кодовые последовательности символов ±1 длительностью 2 T .

Сигнал, созданный согласно вышеприведенного закона, имеет вид, приведенный на рис. 1.

При использовании семейства сигналов МЧМ в радионавигации приемное устройство

При использовании семейства сигналов МЧМ в радионавигации приемное устройство должно осуществлять измерение фазового сдвига и амплитуду сигнала.

Оптимальный приемник такого сигнала осуществляет перемножение принимаемого сигнала на синусную и косинусную копии, накопление полученных значений и последующее вычисление оценки угла фазового сдвига и оценки амплитуды сигнала по формулам

Рис. 1. Вид сигнала МЧМ

ф = arctan

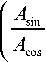
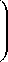
A 1 =   A s²in + A c²os

где ф - фазовый сдвиг принимаемого сигнала относительно опорного сигнала приемника.А^ - интегральное значение синусной составляющей; А - интегральное значение косинусной составляющей; А ₁ - измеренная величина первой гармоники принимаемого сигнала.

Недостатком прямой цифровой реализации оптимального метода является большое количество операций умножения, которое требуется выполнять для каждой выборки сигнала, что усложняет реализацию приемного устройства.

Сократить количество выполняемых операций умно жения можно, если предварительно попериодно накапливать принимаемый сигнал.

Оценка угла фазового сдвига находится из следующе го соотношения:

р= arctan

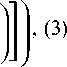
M2

p - i

I Si sin i=0

/

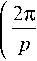
p - 1 I i = 0

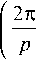
A 1

'c I ² • P I S i • sin I — to I p

M2

p-1          (П у I 2•

+ > 5 • COSI —

i i=оI

,(4)

где   S_j   - z -ая выборка сигнала   S( t ),

, Д   ( T ■ z

= IS — + Tj j=0 V p

S i

)

, k = 1,2,... - число периодов

J

сигнала, укладывающихся во времени измерения.

Для того чтобы применить указанный метод оценки параметров сигнала для оценки сигнала МЧМ, необходимо сформировать сигнал дискретизации, пропорциональный мгновенным частотам МЧМ сигнала. Его формирование осуществляется цифровым синтезатором частоты (рис. 2).

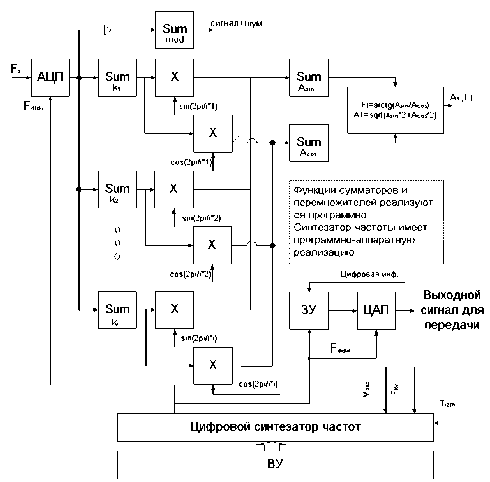
Рис. 2. Функциональная схема устройства

При такой дискретизации сигнала снимается частотная модуляция псевдослучайной последовательности (ПСП). Полученные выборки сигнала попериодно накапливаются. После окончания измерительного периода, накопленные значения выборок сигнала, представляющие собой значения выборок за один период, умножаются на значения выборок в периоде синусной и косинусной составляющей. Полученные значения суммируются сумматорами соответственно синусной и косинусной составляющих. Оценка величины фазового сдвига вычисляется по формуле (1), а оценка амплитуды первой гармоники сигнала по формуле (2).

Точное знание временного положения выборки сигнала, соответствующего ряду фазовых сдвигов на периоде сигнала, позволяет легко сформировать точную копию сигнала МЧМ, необходимую для передачи. Для этого нужно подать на цифровой аналоговый преобразователь (ЦАП), тактовой частотой которого является сформированная частота дискретизации, значения выборок на периоде гармонического сигнала. Значения выборок на периоде сигнала могут быть вычислены заранее и записаны в запоминающем устройстве. При расчете значений выборок учитываются погрешности, вносимые последующими фильтрами и передатчиком.

Погрешности в точности формирования временного положения сигнала дискретизации определяют погрешности измерения фазового сдвига и амплитуды первой гармоники сигнала.

Временное положение выборок рассчитываются из формулы формирования входного сигнала. Как известно сигнал, МЧМ - это последовательность сигналов двух частот, периоды которых рассчитываются согласно формуле T ₁ = 2TT / (2TT + D(t)T_s 1 2), где D(t) - значение модифицированной ПСП, принимающей ±1; T - период опорной частоты входного сигнала, T_psp - половина длительности символа ПСП.

Модифицированная ПСП D ( t ) образована из кодовых последовательностей C ( t ) и 5 ( t ) .

Рассмотрим программно-аппаратный метод реализации синтезатора частоты дискретизации. Аппаратная часть синтезатора состоит из счетчика тактовой частоты и регистра выборки (рис. 3). Счетчик записывает новое значение из регистра после формирования каждой выборки частоты дискретизации. Значение регистра определяется вычислительным устройством (ВУ) в период между формированием выборок частоты дискретизации. Следует отметить следующую особенность: частота квантования F должна быть пропорциональна несущей частоте входного сигнала.

К особенностям формирования частоты дискретизации таким методом следует отнести высокую выходную частоту синтезатора и, как следствие, малое время на выполнения компьютерных обработок. Особенности формирования частоты дискретизации программноаппаратным методом приведены в алгоритме на рис. 4. Граница символа ПСП не совпадает с границей частоты дискретизации, причем она проходит между двумя импульсами частоты дискретизации случайным образом. Среднее значение периода формирования импульсов частоты дискретизации будет соответствовать расчетно- му, а мгновенное будет отличаться на значительную ве личину.

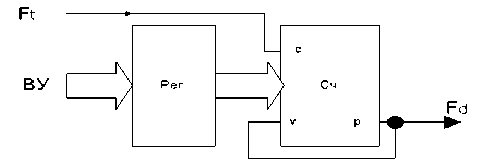
Рис. 3. Аппаратная часть синтезатора частоты

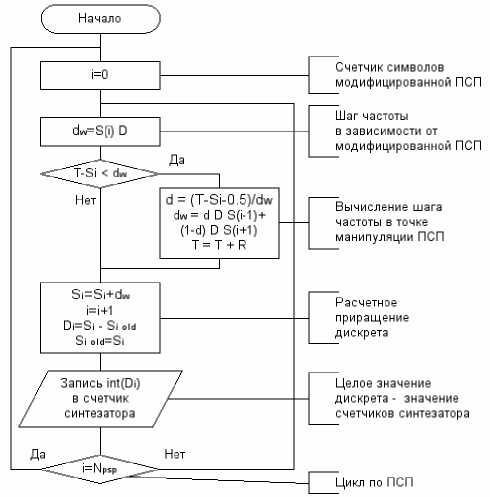
Рис. 4. Алгоритм формирования частоты дискретизации программно-аппаратным способом

Вычисление временного положения импульса частоты дискретизации на момент манипуляции ПСП может осуществляться не в реальном масштабе времени.

Фактическое временное положение сформированного импульса частоты дискретизации зависит от отношения F j F_dkr и не соответствует его расчетному значению. Возникают шумы, вызванные неточностью мгновенного положения импульса дискретизации. Влияние точности формирования выборки сигнала на точность измерения фазового сдвига будет рассмотрено в дальнейшем.

Исследования проводились при помощи компьютерной вычислительной модели. В качестве ПСП использовались следующие последовательности:

ПСП1:[-1 1-111-1-11-1-1-111 11-1],

ПСП2: [-1-11111-1-11111-1-111].

Точность формирования выборки определялась отношением количества исследуемых выборок на периоде сигнала к количеству выборок АЦП на периоде сигнала: R=N_kIN„.

Важнейшей характеристикой ортогонального фазометра МЧМ сигнала является оценка значения погрешности измерения фазового сдвига, зависящая от величины фазового сдвига входного сигнала (рис. 5). Во время исследования изменялось значение фазового сдвига при неизменной величине задержки сигнала. Зависимость характеризует минимально возможные погрешности устройства. При исследовании задавались следующие параметры: количество измерительных точек на периоде сигнала - 80; количество импульсов дискретизации - 4, соответственно точность выборки равна R = 20. Разрядность АЦП не устанавливалась.

Реальное значение погрешности, зависящей от величины фазового сдвига, мы получаем, когда фазовый сдвиг образуется путем задержки ПСП. Соответствующие зависимости при разных значениях точности формирования выборки сигнала приведены на рис. 6. Как видно из приведенных характеристик, зависимость существенно изменяется, что вызвано дополнительной погрешностью, вносимой при манипуляции ПСП, и, как следствие, ошибкой в формировании времени импульсов дискретизации для части периодов сигнала.

Зависимости погрешности фазового сдвига от количества выборок на периоде сигнала при различных значениях точности формирования выборки R = N_k/N_v, определяющие требования к синтезатору частоты дискретизации, несущественны. Это происходит за счет усреднения значений выборок сигнала.

Для исключения влияния точности формирования частоты дискретизации на погрешность измерения угла фазового сдвига от количества импульсов дискретизации на периоде сигнала, измерения проводились при фиксированном значении точности R (рис. 7). Величина фазовой погрешности снижается при восьми и более импульсов дискретизации на периоде сигнала, но не является существенной величиной и при минимальных значениях.

Накопление выборок сигнала существенно снижает требования к разрядности АЦП, что видно из зависимости ошибки измерения фазового сдвига от разрядности АЦП (рис. 8).

Тем не менее, проведем исследование зависимости влияния разрядности АЦП на измерение амплитуды сигнала, которая также существенна (рис. 9).

Из приведенных графиков видно, что для высокоточного измерения амплитуды сигнала АЦП достаточно иметь 10 разрядов.

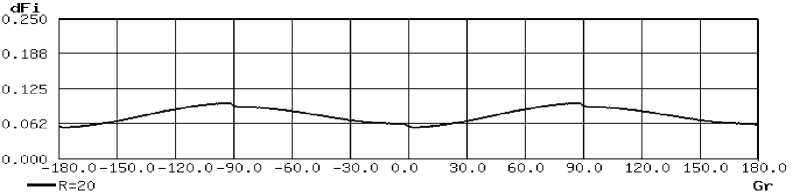
Рис. 5. Зависимость погрешности измерения фазового сдвига от величины фазового сдвига

Измерение амплитуды сигнала важно для устранения неоднозначности измерения фазового сдвига и поиска сигнала ПСП. Автокорреляционная функция, полученная при измерении амплитуды сигнала, приведена на рис. 10. Значительная величина боковых лепестков активно-коррекционной функции (АКФ) вызвана упрощенной ПСП, использованной при исследовании характеристик устройства, что не влияет на параметры устройства, полученные при измерении фазовых погрешностей.

Предложенный способ оценки параметров МЧМ сигнала позволяет применять устройство в приемниках радионавигационных систем, обладает высокой точностью и помехоустойчивостью, но имеет недостатки при практическом применении устройства: он не позволяет выполнять параллельную обработку множества сигналов, необходимую при поиске и обнаружении сигналов с большой базой и малым отношением сигнал-шум.

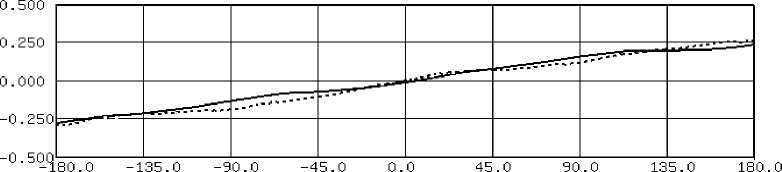
.....R=5 ---R = 50                                                                     Gr

Рис. 6. Зависимость измерения фазового сдвига от точности формирования частоты дискретизации

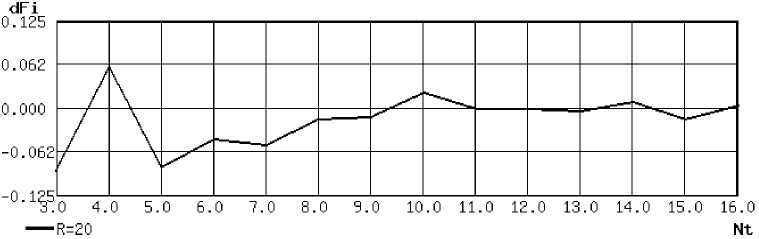
Рис. 7. Влияние на фазовую погрешность количества импульсов дискретизации на периоде сигнала

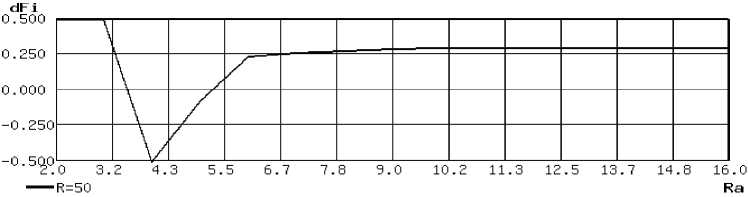
Рис. 8. Зависимость значения фазовой погрешности от разрядности АЦП при ф = 0 °

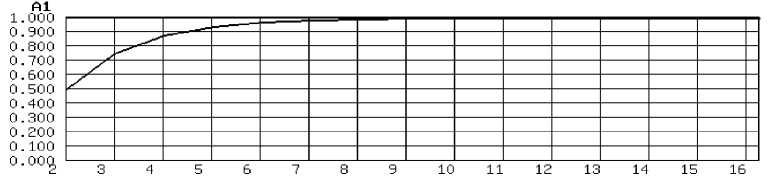
---R = 20

Рис. 9. Зависимость значения измеренной амплитуды сигнала от разрядности АЦП

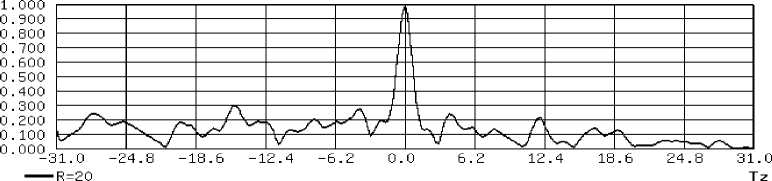
Рис. 10. Автокорреляционная функция сигнала на периоде ПСП, полученная при измерении амплитуды

При рассмотрении схемы параллельного приемника обратим внимание на несущественную величину фазовой погрешности при различных значениях точности формирования выборки сигнала (рис. 6).

Параллельный приемник в отличие от последовательного высокоточного приемника в параллельном приемнике применяется два АЦП, на которые подаются частоты дискретизации, пропорциональные частотам сигнала.

Коммутация выборок сигналом модифицированной ПСП осуществляется после аналого-цифрового преобразования сигнала. Различие параллельных каналов приемника состоит в том, что модифицированная ПСП подается на каждый из каналов с задержкой на величину бита ПСП. Этим же сигналом переключается частота дискретизации каждого сумматора.

В каждом из каналов производится накопление и выборок в периоде сигнала, и - должно быть четным числом > 2. По окончании измерительного периода накопленные значения выборок на периоде сигнала перемножаются на синусную и косинусную составляющие опорного сигнала. Полученные значения выборок синусной и косинусной составляющих сигнала суммируются. Оценка угла фазового сдвига и амплитуды первой гармоники осуществляется по формулам (1) и (2).

Также как и в предыдущей схеме (рис. 2), выборкам частоты дискретизации должен соответствовать определенный фазовый сдвиг. Он должен быть одинаковым для разных значений частоты сигнала в битах ПСП. В устройстве (рис. 11) сигнал частоты дискретизации образуется простой коммутацией частот, пропорциональных частотам спектра сигнала. В начале измерительного периода делителей частот дискретизации сбрасываются.

Расстановка импульсов частоты дискретизации на периоде, согласно заданных фаз, будет осуществляться автоматически при условии, что количество импульсов дискретизации на периоде является четным.

Функциональная схема синтезатора частоты, поясняющая принцип его работы, приведена на рис. 12. Коды делителей частоты для формирования частот дискретизации F_d^_k1 и F_ddd заносятся вычислительным устройством (ВУ) в регистры и переписываются в делители сигналом переполнения счетчиков. Для формирования меандра на выходе делителей частоты стоят делители на два. Коды частоты, записываемые в регистры, имеют, соответственно, уменьшенное вдвое значение. Полученные частоты используются для дискретизации АЦП (рис. 11) и для формирования сигналов стробирования накопителей выборок в каналах. С этой целью создаются сигналы F _dl._{$^r (канш 1)} и другие путем коммутации на логических элементах. Сигналами коммутации служат задержанные сигналы модифицированной ПСП.

Для сравнения параметров параллельного приемника рассмотрим зависимость погрешности оценки фазового сдвига, зависящую от величины фазового сдвига входного сигнала при неизменной величине задержки ПСП (рис. 13).

Исследование проводилось при различных значениях точности формирования опорного сигнала: R = Т _сигн/ Т _дискр, где Т _сигн- длительность периода сигнала, Т _дискр - длительность периода частоты дискретизации.

На графике видно, что в отличие от схемы последовательного приемника при увеличении R (точность фор-

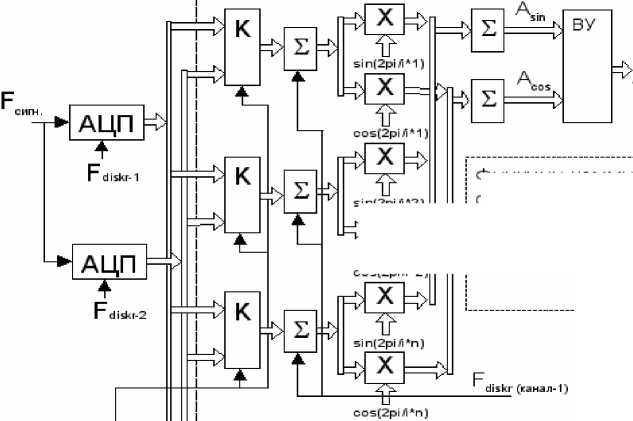
5in(2pi/l"2)

Функции коммутаторов (К), сумматоров (Е) и перемножителей (X) реализуются программно.

Fi=arctg(As:n/Acos)

A^sqrttA^+AV)

oos(2pi/1*2)

Канал 1

Ft

Канал 2

Ft

Канал N

Модифицированная ПСП

Рис. 11. Функциональная схема устройства мирования умноженного сигнала), величина фазовой погрешности существенно уменьшается. Значение фазовое погрешности для параллельного приемника при А = 20 совпадает со значением фазовой погрешности последовательного приемника (рис. 5).

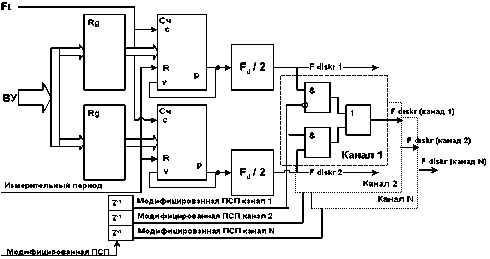
Рис. 12. Функциональная схема синтезатора частоты

Максимальное значение погрешности, зависящей от величины фазового сдвига и задержки ПСП (рис. 14), не отличается от соответствующего значения, полученного при исследовании параметров последовательного приемника (рис. 6). Но существенно меняется вид этой зависимости.

Как видно из приведенной характеристики, зависимость существенно изменяется, что вызвано дополнительной погрешностью, вносимой при манипуляции ПСП, и, как следствие, ошибкой в формировании времени импульсов дискретизации для части периодов сигнала.

Прочие зависимости устройства параллельного приемника также несущественно отличаются от параметров, полученных при исследовании последовательного приемника.

Сравнительный анализ схем последовательного и параллельного приемников показывает, что параллельный приемник имеет более простую реализацию синтезатора опорного сигнала при одинаковых метрологических параметрах, но при этом накладываются некоторые ограничения на выбор частот, на которых должно работать радиотехническое устройство. Так является недопустимым применение трех импульсов дискретизации на периоде сигнала. Их количество должно быть не меньше четырех, причем число должно быть четным. Накладываются так же ограничения на выбор количества периодов сигнала на одном бите модифицированной ПСП. Важным является то, что отношение длительности ПСП к длительности сигнала (TIT не должно быть кратным.

Указанные особенности параллельного приемника накладывают ограничения на возможности его применения.

В целом же применение приведенных схем позволяет применить методы оптимальной обработки сигналов в корреляционном приемнике радионавигационной системы при сравнительно небольших затратах на оборудование и вычислительные мощности.

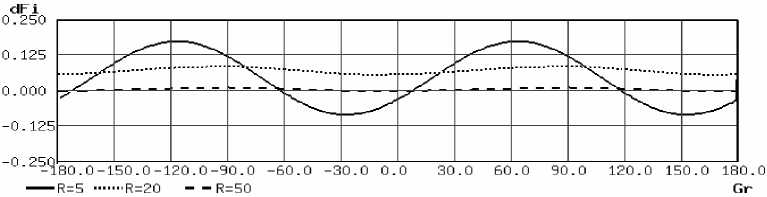
Рис. 13. Зависимость погрешности измерения фазового сдвига от величины фазового сдвига

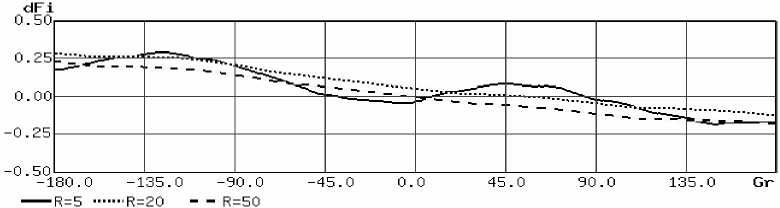
Рис. 14. Зависимость фазовой ошибки от величины задержки, выраженной через величину фазового сдвига

MINIMAL FREQUENCY MODULATION SIGNAL RECEIVER

The consecutive and parallel schemes ofminimalfrequency modulation signal receiver are considered on the basis of optimal methods. The set errors are investigated while measuring amplitude and phase shift.