Приемные векторы мюонного телескопа станции космических лучей «Новосибирск»

Приемные векторы были рассчитаны ранее для нейтронных мониторов [Mori, 1968a; Yasue et al., 1982; Григорьев, Чирков, 1978] и мюонных телескопов [Mori, 1968b; Григорьев и др., 2007]. Большая часть мюонных телескопов сети станций космических лучей (КЛ), для которых были выполнены расчеты приемных векторов, в настоящее время не работает. В последние годы появился ряд новых, более совершенных детекторов, которые, к сожалению, используются ограниченно из-за отсутствия для них приемных коэффициентов. К таким детекторам относится и матричный телескоп в Новосибирске. Много- канальный наблюдательный комплекс КЛ (МНККЛ) в Новосибирске [Янчуковский, 2010] функционально включает в себя нейтронный монитор 24NM-64, спектрограф, использующий эффект локальной генерации нейтронов [Янчуковский, Янчуковский, 1982; Янчу-ковский, Филимонов, 2000], и матричный мюонный телескоп [Янчуковский, 2006а]. Матричная структура обеспечивает создание в одном пункте целой системы многонаправленных мюонных телескопов. Для наблюдения анизотропии КЛ мюонные телескопы более пригодны, чем нейтронные мониторы, поскольку являются узконаправленными. Определение анизотропии и градиентов КЛ с энергией 1–250 ГэВ необходимо для разработки методов диагностики межпланетной среды по данным наземных наблюдений КЛ. Метод глобальной съемки, разработанный в ИКФИА СО РАН [Крымский и др., 1966], позволяет определять анизотропию КЛ в каждый момент времени и делает возможным исследование быстрых флуктуаций анизотропии, связанных с динамикой межпланетной среды. Он объединяет три метода [Белов и др., 2004]:

– метод коэффициента связи [Дорман, 1957];

– метод траекторных расчетов движения частиц в магнитном поле Земли [Дорман и др., 1971];

– метод сферического анализа, позволяющий выделить сферические гармоники для дальнейшего анализа [Колмогоров, Фомин, 1989].

Коэффициентами гармоник являются коэффициенты приемных векторов детекторов КЛ и вектор, характеризующий анизотропию КЛ в межпланетном пространстве.

МЕТОД ПРИЕМНЫХ ВЕКТОРОВ

Интенсивность КЛ, регистрируемая некоторым прибором в атмосфере, определяется его приемными характеристиками, отражающими геометрию и географическое положение прибора и тип наблюдаемых вторичных частиц. Для учета влияния этих параметров в ИКФИА СО РАН был разработан метод приемных векторов [Кузьмин, 1968].

Распределение КЛ по сфере I (θ, φ) за пределами магнитосферы можно представить разложением в ряд по системе сферических функций, являющихся решениями уравнения Лапласа:

I ( e , ф ) =

„ „                                                  (1)

= E E ( a nm cos ( ^m ф )⁺ b n sin ( ^m ф ) ) P m ( sin v ) , n = 0 m = 0

где θ, φ — широтный и долготный углы в некоторой системе координат, P n^m ( sin ф) — присоединенные функции Лежандра. Это распределение удобно представить в виде многомерного вектора J = { a ^m , b m } c бесконечным числом компонент 0 ≤ m ≤ n ≤ ∞. Тогда для каждого точечного прибора можно определить приемный вектор R такой, что интенсивность I , регистрируемая прибором, равна скалярному произведению:

I = J? R.                                            (2)

Из приведенных уравнений следует, что

R = { х П , У П } , где х П = cos ( m ф ) P „^m ( sin ф ) ; y m = sin ( m ф ) P m ( sin ф ) .

Для нахождения приемных векторов реальных приборов должны быть известны: диаграммы направленности детектора N (θ, φ), коэффициенты связи W ( E ) между вторичными и первичными частицами, энергетический спектр f n ( E ) исследуемых вариаций КЛ и асимптотические углы прихода частиц Ψ( E , θ, φ), Ф( Е , θ, φ). При разложении распределения КЛ по сферическим функциям ряд быстро сходится. Поэтому, кроме изотропной составляющей, обычно учитывают первые две гармоники распределения, эффекты от которых наблюдаются в эксперименте. В соответствии с этим в векторах A и R учитываются девять первых компонент.

Расчет приемных векторов проводится ниже для системы многонаправленных узкоугольных мюонных телескопов МНККЛ в Новосибирске. Регистрация мюонов КЛ осуществляется с помощью матриц детектирования, реализованных на основе газоразрядных пропорциональных счетчиков СГМ-14 [Янчуковский, 1994]. Выделение частиц по направлениям прихода производится путем 4-кратных совпадений сигналов в счетчиках четырех слоев, размещенных по два слоя над и под нейтронным монитором (рис. 1).

Счетчики, объединенные в детекторные блоки по три, в слоях расположены взаимно перпендикулярно и при включении их в схемы совпадений образуют площадки детектирования размером 45×45 см (рис. 2).

Направления, по которым рассчитываются приемные векторы мюонных телескопов на газоразрядных счетчиках, определяются схемами совпадений и ориентацией прибора. Для комплекса мюонных телескопов Якутского спектрографа были выбраны следующие направления: вертикаль и зенитные углы 30°, 60° с севера и юга [Григорьев и др., 2007]. Комплекс мюонных телескопов установки КЛ в Новосибирске, где применен матричный метод детектирования с 4-кратными совпадениями, позволяет проводить регистрацию частиц по вертикали и под зенитными углами 26, 35, 44, 55, 63°. При этом азимутальные направления регистрации для этих зенитных углов обусловлены ориентацией секции нейтронного монитора, на котором расположен телескоп, и имеют направления N (север), S (юг), W (запад), E (восток) и промежуточные азимутальные направления NW, WS, SE и EN.

ДИАГРАММЫ НАПРАВЛЕННОСТИ

Каждый прибор при регистрации КЛ ориентирован в область небесной сферы, определяемую его диаграммой направленности N (θ, φ) d ω, где ω — телесный угол [Кузьмин, 1964]. В диаграмме направленности находят отражение как геометрические особенности прибора, так и зенитно-азимутальная

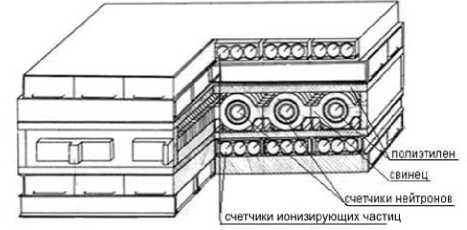
Рис. 1. Расположение счетчиков ионизирующих частиц телескопа в секции нейтронного монитора

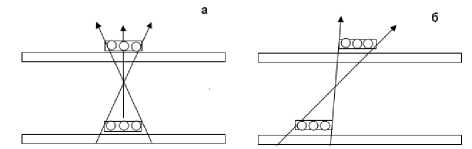
Рис. 2. Схематическое представление 4-кратных совпадений при регистрации частиц с вертикального направления ( а ) и с направления в 26° от вертикали ( б )

угловая зависимость интенсивности регистрируемых частиц [Кузьмин, 1968].

Угловая зависимость интенсивности КЛ определяется выражением

I (θ)= I 0 cos^γθ,

где I 0 — абсолютная интенсивность частиц, приходящих с вертикального направления, которая составляет 0.5 см^–2 мин^–1 ср^–1 [Мурзин, 1970], γ — показатель степени углового распределения частиц (для поверхности Земли γ = 1.3). Тогда скорость счета мюонного телескопа N счет находится как

N счет = I 0 C ,

где C называется светосилой телескопа [Кузьмин, 1968] и определяется выражением ф 6

C = Н ^ ( 6 , ф ) cos ^Y+ 1 6 sin 6 d Ф d 6 .                 ⁽⁶⁾

Здесь S (θ, φ) — площадь, пересекаемая частицами при регистрации совпадений в выбранном направлении, в зависимости от зенитного θ и азимутального φ углов их прихода. Показатель γ в выражении (6) определяется уровнем наблюдения относительно поверхности Земли. Сторона квадратной ячейки детектирования L =45 см, а расстояние между нижним и верхним слоем ячеек, установленных на совпадение, H =103 см (рис. 2). Расчет диаграммы направленности для одного блока детектирования проводится для направлений регистрации под углами к зениту 0, 26, 44, 55 и 63°. Оценка ожидаемых значений темпа счета частиц (без учета массы нейтронного монитора) осуществляется для различных зенитных углов мюонного телескопа. За 0° азимутального угла принимается фронтальное расположение нейтронного монитора в направлении 30° NW.

НАПРАВЛЕНИЕ РЕГИСТРАЦИИ ЧАСТИЦ ПОД ЗЕНИТНЫМ УГЛОМ 0° (ВЕРТИКАЛЬ)

Площадь S (θ, φ), пересекаемая частицами при регистрации совпадений с вертикального направления, для одного блока детектирования находится как

S (θ, φ)=( L – H tgθcosφ)( L – H tgθsinφ),           (7)

где, из условия совпадений, каждый из множителей в скобках не может быть меньше нуля. При расчете диаграммы направленности выбор угла, по которому начинается интегрирование, определяется видом диаграммы — азимутальная или зенитная. Для светосилы телескопа, регистрирующего приход частиц с вертикального направления, имеем:

C верт = |j 5 ( 6 , ф ) cos ^{Y+ 1} 6 sin 6 cos 6 d 6 d ф .      (8)

Дополнительный cosθ учитывает угол между поверхностью верхнего слоя матрицы детектирования и направлением падающих частиц. Телескоп для регистрации частиц с вертикального направления собирает частицы со всех азимутов, в этом случае величина C верт умножается на 4. Учитывая значение I 0 , получим темп счета одного блока N верт =10026 имп/ч. Тогда темп счета телескопа, в который входит 24 блока (одна секция установки), N _в2_е⁴_рт = 240624 имп/ч.

НАПРАВЛЕНИЯ РЕГИСТРАЦИИ ЧАСТИЦ ПОД ЗЕНИТНЫМИ УГЛАМИ 26, 44, 55 И 63°

Для указанных зенитных углов рассмотрим азимутальные направления 30° NW, 30° WS, 30° SE, 30° EN. Площадь S (θ, φ), пересекаемая частицами при регистрации совпадений, для наклонных направлений телескопа будет состоять из двух частей:

S (θ, φ)= S 1 (θ, φ)+ S 2 (θ, φ),                          (9)

где S ₁(θ, φ)=( H tg θ cos φ– r )( L – H tg θsin φ), θ≤θ _T ; (10)

S 2 (θ, φ)=( r 1 – H tg θcos φ)( L – H tg θ sin φ), θ≥θ T . (11) Здесь θ T — зенитный угол оси (направление) телескопа; r , r 1 — наименьшее и наибольшее расстояния в горизонтальной плоскости между сторонами верхних и нижних ячеек, включенных на совпадение. Для углов θ T =26, 44, 55 и 63° имеем r =5, 55, 105 и 155 см, r ₁=95, 145, 195 и 245 см соответственно.

Согласно изложенной выше процедуре расчета темпа счета для телескопа, регистрирующего частицы с вертикального направления, получены ожидаемые значения темпа счета наклонных телескопов N 6 n T (здесь n — общее число пар ячеек, включенных на совпадение, для наклонного телескопа под углом к зениту θ T ):

N ₂ ² ₆ ⁰ (NW, SE)=130700 имп/ч;

N ₂ ¹ ₆ ⁸ (WS, EN)=117630 имп/ч;

N ₄ ¹ ₄ ⁶ (NW, SE)=35060 имп/ч;

N ₄ ¹ ₄ ² (WS, EN)=26300 имп/ч;

N ₅ ¹ ₅ ² (NW, SE)=7800 имп/ч;

N ₅ ⁶ ₅ (WS, EN)=4000 имп/ч;

N ₆ ⁸ ₃ (NW, SE)=1710 имп/ч.

В скобках указаны азимутальные направления телескопов. На рис. 3 представлены зенитные и азимутальные диаграммы направленности для вертикального и наклонных направлений системы мюонных телескопов МНККЛ.

КОЭФФИЦИЕНТЫ СВЯЗИ

Коэффициенты связи W, согласно определению [Дорман, 1957], характеризуют относительную чувствительность детектора к протонам первичных космических лучей различных энергий. Коэффициенты связи для каналов матричного мюонного телескопа МНККЛ находились путем теоретических расчетов [Янчуковский, 1986] и экспериментально [Янчуковский, 2006б; Янчуковский, 2007] методом пробного детектора [Дворников и др., 1989]. Коэффициенты связи, нормированные на 100 %, определялись в виде exp {-d [Ea + b]-c}

W ( E , e_r ) = a---------------:----’^k T’           [ E a + b ] c ⁺ 1

где а — нормировочный коэффициент, который вычисляется как

[- d ( a E + b ) c j

” exp a-1 = J min

( a E + b ) c ⁺ 1

dE .

Здесь и в выражении (12) параметры b , c , d , α, нормировочный коэффициент a и пороговая энергия E min являются функциями θ T (зенитного угла оси телескопа T ). Параметры b , c , d , α определялись методом минимизации функционала [Янчуковский, 2007]. Для получения численных значений коэффициентов связи было использовано выражение (12). При расчетах здесь и далее использовался единый дискретный набор энергий — от пороговой E min (θ T ) для каждого направления θ T регистрации частиц до энергий порядка 1000 ГэВ. Полученные результаты (после нормировки и учета толщины экрана по направлениям) представлены графически на рис. 4.

ТРАЕКТОРИИ КОСМИЧЕСКИХ ЛУЧЕЙ

Расчет траекторий КЛ для ст. «Новосибирск» проводился для того же дискретного набора энергий, который использовался при расчетах коэффициентов связи. Поскольку диаграммы направленности мюонных телескопов имеют также зависимость от азимутального угла (рис. 3), асимптотические углы прихода частиц Ψ( E , θ, φ), Ф( E , θ, φ) рассчитывались с разрешением 8° по зениту (от 0°до 64°) и 10° по азимуту (от 0° до 350°). При этом были использованы коэффициенты разложения главного магнитного поля Земли, представленные 10 гармониками для эпохи 2000 г. [ftp://nssdcftp.gsfc.nasa.gov/models/geomagnetic/igrf/ fortran_code]. Расчеты траекторий КЛ были выполнены согласно методике, изложенной в [Дорман и др., 1971]. При численном интегрировании применялся метод Эйлера, для которого начальный шаг h 0 подбирался эмпирически, исходя из точности решения.

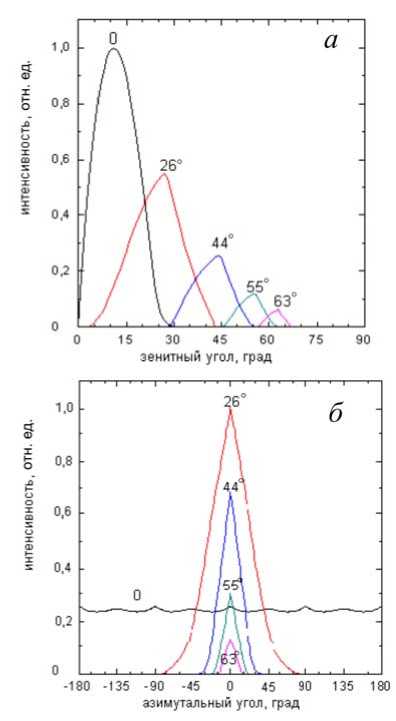
Рис. 3. Зенитные ( а ) и азимутальные ( б ) диаграммы направленности системы мюонных телескопов под углами к зениту 0, 26, 44, 55 и 63°

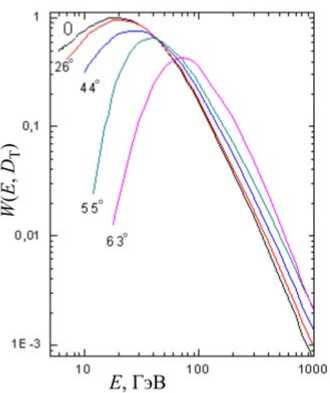
Рис. 4. Коэффициенты связи W ( E, e _T ) для системы мюонных телескопов МНККЛ

Начиная с расстояния 3 r 0 ( r 0 — радиус Земли), вклад в геомагнитное поле гармоник выше второй составляет менее 1 %, шаг h в дальнейшем выбирался как h = h 0 ( r /3 r 0 ). Расчеты траекторий проводились до выполнения одного из условий: r ≤ r 0 , n = 15000, r ≥ 25 r 0 , где n — число шагов интегрирования. Выполнение первых двух условий соответствовало запрещенным

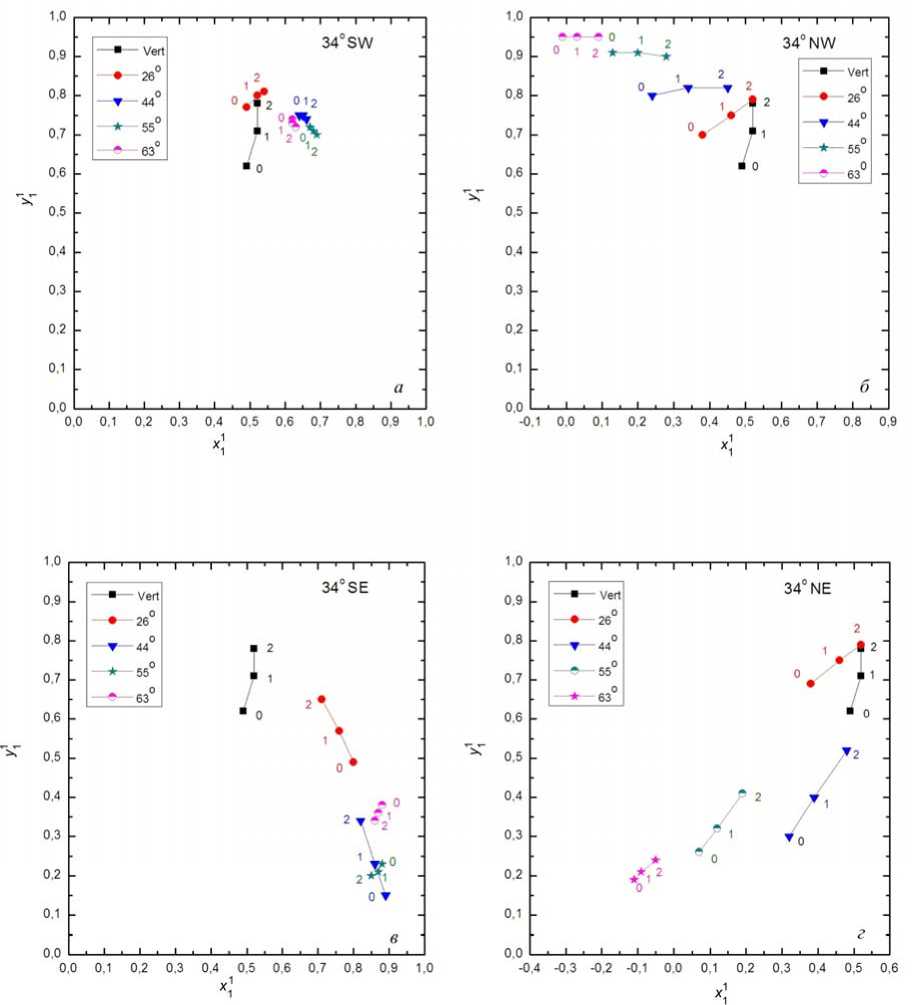
Рис. 5. Компоненты приемных векторов первой сферической гармоники мюонного телескопа КЛ в Новосибирске для азимутальных направлений SW ( а ), NW ( б), SE ( в ) и NE ( г ) для Е ₀ =70 ГэВ, время местное

траекториям. При достижении расстояния 25 r ₀ интегрирование прекращалось и по конечным значениям траектории частицы определялись асимптотические широта Ф( E , 6, ф) и долгота Т( E , 6, ф).

ЭНЕРГЕТИЧЕСКИЙ СПЕКТР

Имеющиеся результаты по определению энергетических спектров первой и второй сферических гармоник распределения КЛ дают широкую область спектральных изменений. Их выбор зависит от поставленных задач по исследованию распределения КЛ с помощью этих гармоник. Для определения компонент первой гармоники выбран спектр f1(E) вида f.(E)~E-Y, если EE0.

Здесь у принимает значения 0, 1, 2, а E ₀ — 30, 70, 150 ГэВ.

Для определения второй сферической гармоники использован вид спектра f₂ ( E ) из работы [Криво-шапкин и др., 1989], где предложен экранировочный механизм его образования. После аппроксимации его можно представить следующим образом:

f;(E) ~ (E/E0), если EE0,                     (13)

где E ₀=30, 70, 150 ГэВ.

ПРИЕМНЫЕ ВЕКТОРЫ

Расчет компонент приемных векторов осуществлялся исходя из выражения [Чирков и др., 1967]:

m Z_n

п го 2 п 2

J J J W ( E ) f n ( E ) W ( 6 , ф ) sin ( 6 ) e im ^Y( E ’ ^6ф) P nm ( sinФ ( E , 6 , ф ) ) dEd 6 d ф

E min 00

п

J J " j W ( E ) f n ( E ) W ( 6 , ф ) sin ( ф ) dEd 6 d ф

E min 00

,

где z m = x m + ty m .

Произведение emY(E’6,ф)Pnm(sin Ф (E, 6, ф)) держит компоненты со-

x ° = sin Ф; x ¹ = cos Ф cos Y ; y 1 = cos Ф sin V ;

x. ¹ = —sin ² Ф —; x 1 = sin2Фcos Y ; у, = sin2Фsin Y ;

x ₂ ² = cos ² Ф cos2 Y ; у 2 = cos ² Ф sin2 Y .

Компонента x ₁ ⁰ характеризует чувствительность данного детектора к вкладу первой гармоники в изотропную составляющую интенсивности КЛ; x ₁ ¹ и y ₁ ¹ — соответственно радиальная и азимутальная компоненты первой гармоники в географической (UT) или собственной (LT) системе координат. Компоненты приемных векторов LT предназначены для анализа данных по местному времени. Для метода глобальной съемки следует использовать компоненты приемных векторов UT (мировое время). Модуль | Z 11| = ^ ( x 11 ) + ( y 11 ) и угол Q 1 = arctg ( y 11 (x \ ) характеризуют наблюдаемые изменения первичных параметров первой гармоники по амплитуде и фазе в зависимости от широты и долготы пункта наблюдения. Изменения амплитуды будут на величину 1/ Z ₁ ¹ , а фазы — на Q ₁ ¹ градусов (т. е. при положительном значении будут смещены на более позднее время). Например, значения приемных коэффициентов мюонного телескопа ст. «Новосибирск» (LT) для вертикального направления для первой гармоники (суточная вариация) составляют x 11 = 0.56 и у 1 = 0.75. В этом случае модуль вектора |Z 11| = 0.936 , а угол Q 1 = 53.3 ° , т. е. наблюдаемая амплитуда будет уменьшена относительно первичной в 1.07 раза, а фаза смещена на 53.3° (на более позднее время).

Компонента x ₂ ⁰ характеризует вклад второй сферической гармоники в изотропную интенсивность КЛ. Составляющие x ¹ ₂ и y ¹ ₂ являются компонентами антисимметричной суточной вариации, обусловленной вкладом второй гармоники в первую. Ее фаза будет противоположна в Северном и Южном полушариях. Соответственно x ₂ ² и y ₂ ² представляют собой компоненты второй сферической гармоники распределения КЛ. Модули Z 21 = ^ ( x 2 ) + ( у 2 ) , I ^Z 221 = ^ ( x 22 ) ^{2 +}( У 22 ) ² и углы Q ¹ = ^arctg ( у 2 / x 2 ) ,

Q 2 = arctg ( у 2/ x 2 ) характеризуют их изменения относительно первичного распределения в зависимости от координат станции КЛ.

В качестве примера на рис. 5, а – г представлены компоненты приемных векторов первой сферической гармоники распределения космических лучей для азимутальных направлений 34° SW, 34° NW, 34° SE и 34° NE (LT) для Е 0 =70 ГэВ и γ=0, 1, 2. Результаты расчета компонент приемных векторов, полученные для первой и второй сферических гармоник распределения КЛ, в цифровом виде представлены в таблицах 1–7 (приложение А).

ЗАКЛЮЧЕНИЕ

Найдены компоненты приемных векторов мюонного телескопа наблюдательного комплекса космических лучей ст. «Новосибирск». При этом были учтены конструктивные особенности установки, ее ориентация, диаграммы направленности в зависимости от зенитного и азимутального углов, коэффициенты связи системы телескопов, найденные экспериментально методом пробного детектора. Представленные приемные характеристики установки необходимы при анализе модуляционных эффектов интенсивности космических лучей в широком диапазоне энергий первичных частиц.