Приэкваториальный резонатор для УНЧ-колебаний с учетом примеси тяжелых ионов в магнитосфере

Данная работа посвящена пространственной структуре ультранизкочастотных (УНЧ) волн в двухкомпонентной космической плазме (протоны и тяжелые ионы). Предполагается, что частота волны одного порядка с гирочастотой тяжелых ионов. В земной магнитосфере этому соответствует диапазон геомагнитных пульсаций типа Рс1 (жемчужины).

В соответствии с принятой моделью жемчужины – это альфвеновские волновые пакеты, которые генерируются энергичными ионами и «бегут» вдоль силовой линии от одной магнитосопряженной точки ионосферы к другой [Гульельми, 1979; Demekhov, 2007]. Однако некоторые данные со спутников противоречат этому [Mursula, 2007], поэтому необходим поиск альтернативных объяснений формирования волн Рс1.

Другое объяснение формирования жемчужин было предложено в работах Дмитриенко и Мазура [Дмитриенко, Мазур, 1983; Dmitrienko, Mazur, 1985; 1992; Дмитриенко и др., 1986]. Они показали, что благодаря конечной инерции иона в области плаз-мопаузы может образовываться резонатор поперек магнитных оболочек. В этом случае структура жемчужин может наблюдаться в результате суперпозиции различных гармоник этого резонатора.

Еще одно объяснение было предложено в работах Гульельми и его соавторов [Гульельми, 1967; Guglielmi et al., 2000; Guglielmi et al., 2001; Guglielmi et al., 2007; Гульельми, 2007]. Здесь в основную картину включено присутствие тяжелых ионов в земной магнитосфере, поскольку ионов кислорода может быть так же много, как и протонов [Yang et al., 2007]. Авторы показали, что в случае квазипродоль-ного распространения ( к _± ^ к ц ) в экваториальной области может быть сформирован продольный резонатор, и предположили, что собственные частоты резонатора могут формировать волновой пакет, перемещающийся между точками отражения в этом резонаторе, а также отождествили период скачка пакета с периодом повторения жемчужин Рс1.

Однако некоторые наблюдения свидетельствуют о сильной поперечной локализации волн Рс1 [Enge-bretson et al., 2002; Mursula, 2007; Yahnin et al., 2007; Engebretson et al., 2008], что означает большую ве- личину модуля поперечной компоненты волнового вектора |к±|. Таким образом, необходимо рассмотрение структуры короткопериодичных УНЧ-волн в квазипоперечном приближении (к± ^ кц). Решению этой задачи посвящена предлагаемая работа. Исследование основано на системе уравнений, полученных в работе [Glassmeier et al., 2003], и частично обобщает результаты статьи [Klimushkin et al., 2006] для случая двухмерной неоднородной магнитосферы с плазмой и неравномерным магнитным полем в радиальном и продольном направлениях.

Основные уравнения

Введем координатную систему {x 1, x2, x3} , ориентированную по силовым линиям. В этой системе координатные поверхности x1 = const совпадают с магнитными оболочками, координата x2 соответствует силовой линии на магнитной поверхности, координата x3 отмечает точку на силовой линии. Поскольку координатная система ортогональна, а недиагональные компоненты метрического тензора равны нулю, обозначим диагональные компоненты как gi , а g i представляют собой коэффициенты Ламэ. Детерминант метрического тензора g = g1g2g3. Верхние и нижние индексы означают контравариантные и ковариантные компоненты вектора соответственно. Они связаны между собой выражением aj = Qj I gj (суммирование по повторяющемуся индексу не подразумевается). «Физические» компоненты вектора (т. е. измеряемые в обычном евклидовом базисе) определяются как aj             j aj = 2— = JgjQ1. Например, элемент физическая gj длина силовой линии, выраженный через соответствующую     координату,     выглядит как dl = dx3 = g3ddx3. В дипольном поле удобно использовать параметр Мак-Илвейна L в качестве радиальной координаты x1 и азимутальный угол φ в качестве азимутальной координаты x2. Таким образом,

= cos⁶ 0

¹ 1 + 3 sin² 0

и

g ₂ = L ² cos² θ

[ д , LT д , + д 2 LP д 2 ] Ф

ω ²

-

dl =Lcosθ 1+3sin2θdθ, где θ – обычная сферическая координата (угол, измеренный вдоль силовой линии) [Leonovich, Mazur, 1993]. Другой выбор дипольных координат представлен в статье [Radoski, 1967].

Рассмотрим УНЧ-волну с частотой ω, распространяющуюся в холодной плазме. В этом случае элементы тензора диэлектрической проницаемости выглядят следующим образом:

ⁱ c ²

■ го2 1

i—, д

С ²

-Пд 2 Ф +

^е и = 1

-

p е

ω ²

-

Z -P^L, ω ²

ε ⊥ = 1

-

ω

Ω

-

i

2 pe Ω ² ce

-

Ω ² pi

^Z ®-- 2i ’

+ д , LT g^ д ₂

-

g

∆ _⊥ ^{g 3} ∆ _⊥ Ψ+

g

д 2 L L р g^ д , Ф ;

g

+ д , ^g L T ' д , + д ₂      LP

ω ²

" д 2 Ф

-

Ω η = - ^ce

ωω

Ω

² pe

-

Ω ² ce

+ Z - i ωω

Ω

² pi

-

2, ci

где Ωp и Ωc соответственно электронные (индекс e) и ионные (i) плазменная и циклотронная частоты. Если частота существенно ниже, чем гирочастота электронов Ωce, а также присутствуют два типа ионов – протоны (индекс р) и тяжелые ионы (индекс h), тензор диэлектрической проницаемости перепишется в виде е1 = -~,

ε _⊥ =

η=

22 pp             ph

_{2      2} + _{2      2},

Ω _cp - ω Ω _ch - ω

22  2

pe cp pp          ch ph

-

-

ωΩ ω Ω ² -ω ²    ω Ω ² -ω ^{2 .}

ce               cp                       c

Из уравнений Максвелла мы выведем уравнение для электрического поля E волны с частотой ω:

го ² —           —

₂ ε ˆ E = ∇×∇× E .

c

В общем случае уравнение (1) – это система дифференциальных уравнений в частных производных для двух компонент электрического поля E = ( E ₁, E ₂, 0) , где E ₁ и E ₂ – компоненты, перпендикулярные к равновесному магнитному полю B 0 . Продольная компонента электрического поля равна нулю, поскольку £ | = -^ . В соответствии с теоремой Гельмгольца произвольный вектор поля может быть разложен в виде суммы потенциальной и вихревой компонент [Morse, Feshbach, 1953]. Применяя эту теорему к вектору двухмерного поля E , раскладываем

—

—

^_

E = -V_AФ + V₁x ^_ ф ,

—

где _ = B 0 / B 0 , V_± - двумерный оператор в плоскости ( x ¹, x ²). В однородной плазме волновые функции Φ и Ψ описывают моды альфвеновской волны и быстрого магнитного звука (БМЗ) соответственно [Климушкин, 1994]. В данном случае первую моду (Φ) называют управляемой, а вторую (Ψ) – изотропной модой. Тогда уравнение (1) превращается в систему двух уравнений на функции Φ и Ψ:

- i ₂ c

∂ 1 ^η ∂ 2

g ₃

-

∂ 2 ^η ∂ 1

g ₃

-

. го2 .

• i —г д

С ²

+ д 2 ^

g

- пд 2 Ф +

ˆ

-

д , g^Lр д 2 Ф .

g

Здесь ∆ _⊥ ≡ ∂ ₁

Г. ^

V Vg 7

∂ ₁ +∂ ₂

V Т₉ 7

∂ ₂ – поперечный

лапласиан, а операторы

L ^ˆ T =∂ 3 ^{g 2} ∂ 3 + ^g ε ⊥ ^ω ₂ , g       ^g 1      ^{c 2}

ˆ       g1        g

LP = ∂3    ∂3 +ε g      g2

называются тороидальным и полоидальным операторами соответственно. Подробный вывод системы (3), (4) см. в работе [Glassmeier et al., 2003]. В случае однородной плазмы эта система преобразуется в известное дисперсионное соотношение [Гульельми, 1979]:

ω ²

2 ^ε ⊥ c

-

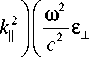
k"

-

k

⊥

ω ⁴

⁼   4 ^η

c

,

где k | и k _± - продольная и поперечная компоненты волнового вектора относительно равновесного магнитного поля.

Продольная структура: области прозрачности и непрозрачности

В поперечном ВКБ-приближении волновое возмущение имеет вид exp[ k 1 ( x ¹) dx ¹+ k 2 x ²], где k 1 и k 2 – радиальная и азимутальная компоненты поперечного волнового вектора соответственно. Здесь предполагается аксиальная симметрия, благодаря которой в качестве координаты x ² может быть использован азимутальный угол φ, а азимутальное волновое число играет роль азимутальной компоненты волнового вектора k ₂. Квадрат поперечного волнового вектора выражается как

2   k12

k⊥ =   + g1

Рассмотрим случай квазипоперечного распространения ( к _± » к ц).

Для начала рассмотрим тороидально поляризованную волну, когда к 1 » к ₂. Тогда система (3), (4) может быть записана в виде

L ^ˆ T ( ω ) φ = i ^{ω g 2} ηΨ , c ² g ₁

где ± l_I – точки пересечения силовой линии с ионосферой.

Поскольку операторы L ^ˆ _T и L ^ˆ _P различны, уравнения (9), (10) имеют различные собственные функции. Однако квадрат продольного волнового вектора ( к = к \| = к ₃ / л[д" 3 ) в продольном ВКБ-прибли-жении одинаков для обеих мод:

k ²

ω ²           ω ²

2 ⁺           2

A p ²(1 -^ω 2 )   A h ²(1 -^ω 2 )

^Ω cp           ^Ω ch

.

- k 1 ^{2 g 2 g 3} Ψ=- i ^ω 2   ^{g 2} ηΦ .

g g          c ²    g ₂

Здесь A _p,h – альфвеновские скорости, определенные для протонов и тяжелых ионов соответственно:

Выражая Ψ из второго уравнения и подставляя в первое, получаем

^A p,h ⁼

⁴ π n p,h m p,h

42 L ^ˆ _T ( ω ) Φ+ ₄ g η ₂ Φ= 0. ck

Таким образом, получено уравнение, описывающее продольную структуру волны в квазипоперечном пределе:

А

L_T ( ω ) Φ = 0.

Применяя аналогичные рассуждения для полои-дально-поляризованной волны ( к 2 ^ к 1 ), получаем уравнение

л

L_P ( ω ) Φ = 0.

Следует заметить, что волновые уравнения (9), (10) не содержат диагональных членов тензора диэлектрической проницаемости η. Это отличает данные уравнения от тех, что были использованы в работах [Guglielmi et al., 2000, 2001; Гульельми, 2007], так как там рассматривался случай к _± / к \ ^ 0 . Tогда дисперсионное соотношение (7) принимает форму

ω2 c; ^£i- ^к \ I

ω ⁴

= ₄ η ². c

где n p, h и m p, h – концентрации и массы протонов и тяжелых ионов.

Заметим, что Ω cp >>Ω ch . Гирочастоты Ω cp и Ω ch зависят от продольной координаты 1 ц . Случай, когда ω<Ω ch на протяжении всей силовой линии соответствует обычной МГД-волне, в отличие от случая ω>Ω cp . Следовательно, наибольший интерес вызывает случай, когда частота волны ниже гирочастоты протонов ω<Ω_cp. На силовой линии всегда имеется точка, где частота волны становится равной гирочастоте тяжелых ионов ω=Ω ch и продольный волновой вектор стремится к бесконечности, k ² → ∞ . Назовем ее точкой сингулярности l_s .

Напомним, что магнитное поле на экваторе минимально. Таким образом, удаляясь от экватора вдоль силовой линии, оказываемся в точке сингулярности, где k ²→–∞. На экваторе оба условия из уравнения (12) положительны до тех пор, пока k ²>0. Поэтому где-то между экватором и точкой сингулярности должна быть точка, где k ²=0, которую назовем точкой отражения l 0 . Ее положение определяется уравнением ω=Ω 0 ( l ), где Ω 0 – частота отражения

А

Ω 0 ² = Ω c ² h

ω ²

Его два решения к |2 ± = — (е ^ ±п ) соответствуют уравнению 4 из работы [Guglielmi et al., 2001]. В случае, рассматриваемом нами ( к _± / к ц » 1), дисперсионное соотношение (7) принимает вид

^{1 + p} h ,

V ^p p 7

_ω 2        ₂

"Т е к\\

η ² ω ⁴

k _⊥ ² c ⁴

что соответствует уравнению (8) или его полои-дальному аналогу, а в пределе к _± / к ц ^ ^ переходит в уравнение (9) или (10).

Перейдем к граничным условиям на ионосфере. Для простоты рассматриваем идеально проводящую ионосферу, тогда граничные условия для потенциала запишутся в виде

где ρ_h,p = n _h,p m _h,p – плотности тяжелых ионов и протонов [Klimushkin et al., 2006]. Здесь для простоты предполагается, что тяжелые ионы в магнитосфере обычно составляют малую примесь к протонам, а их массы приблизительно в десять раз больше.

Итак, вблизи экватора находится резонатор, ограниченный двумя точками отражения ± l 0 (предполагается симметрия север–юг). Далее следуют две непрозрачные области с точками сингулярности в качестве внешних границ. Затем расположены две прозрачные области, каждая из которых ограничена ионосферой Северного и Южного полушарий (рис. 1).

Φ_{± lI} = 0,

Экваториальный резонатор

Экваториальный резонатор служит резервуаром энергии. Его собственная частота определяет частоту возбуждаемой в нем волны.

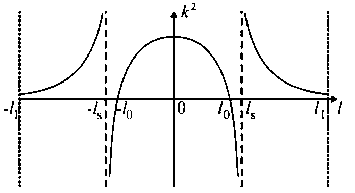
Рис . 1 . Квадрат продольного волнового вектора k ² как функция продольной координаты l .

Вблизи экватора разложение в ряд k ²( l ) выглядит как

. 2            2    ^{1 д} ( k )

k О ¹ ) = k eq ⁺ 2 —^2"

l ², eq

где индекс eq означает экваториальное значение. Точка отражения определяется из 1 0 ( и n ) = ^- 2 k _e²_q / ( k _e ² _q ) ” . Собственная частота ω _n , где n – продольное волновое число, получается из правила квантования Бора– Зоммерфельда:

1 0 (^И n )

I 1

J    k ( to n ) dl = ^п I n ⁺ 2

^{- 1} 0 ^{( и} n )                       ^

После интегрирования получаем

И

2 n

1 ₊ P h O h + ( 2 n + 1 ) P h V о O ' A _h.

I    P p J                 P p

Здесь предполагается, что Och ^ и ^ Ocp. Для всех переменных, зависящих от продольной координаты (Och, Ah p, ph p), взяты экваториальные значения. Штрих означает дифференцирование по продольной координате ((...)' = д(...)/д 1). Следует за- метить, что спектр (16) качественно совпадает со спектром, полученным для квазипродольного приближения (например уравнение (63) из работы [Гульельми, 2007]).

Спектр частот очень плотный: |to _{n + 1} -и _n | ^ и _n . Поскольку в реальности все существующие гармоники резонатора возбуждены, в результате формируются биения. Полуширина резонатора определяется выражением

( 1 n + 1 ) A T

0 " req^ (1 +Рр/Ph )Och req’ а точка сингулярности выражением

12     ¹²

1S ” reqV2 [(1 +Ph/ Pp ) — 1] , где req – экваториальный радиус кривизны силовой линии. Сделаем несколько количественных оценок. Учитывая, что в качестве тяжелых ионов на Земле выступает кислород О+, и принимая Ah=Ap=103км/с, а L=6.6, для основной гармоники (n=0) получаем результаты: ω0≈0.875 рад/с, l0≈0.23req=0.5RE и lS=0.9req. При этом по порядку величины это совпадает с результатами работ [Guglielmi et al., 2000, 2001; Guglielmi, Kangas, 2007; Гульельми, 2007; Lundin, Guglielmi, 2006].

В заключение следует сказать, что для использования правила квантования Бора–Зоммерфельда (15) следует предположить, что резонатор хорошо отделен от областей прозрачности, которые находятся вблизи ионосферы. Фактически это предположение необходимо для использования ВКБ-приближения. В этом случае отдаленные от резонатора области прозрачности вносят экспоненциально малые поправки в значения для собственных частот. Противоположный случай (близкие области прозрачности) требует численных расчетов и отдельного рассмотрения.

Околоионосферные области прозрачности

Заменим продольную координату x ³ на ξ следующим образом:

d ^ = ^Zg dx ³.

g ₂

В результате уравнение (9) принимает вид:

--_Г + V ©Ф = 0,                     (17)

д5

где функция

V © = g 2 ^e±”T g ₁      c ²

ведет себя приблизительно как k2(l) на рис. 1. Решим это уравнение, используя ВКБ-приближение для области, заключенной между ионосферой и точкой сингулярности; переобозначим частоту волны, которая определяется резонатором, как ω=ωn, а граничное условие по-прежнему задается уравнением (11). Заменим также начало продольной координаты, пусть –ξI=0. Тогда ВКБ-решение запишется в виде ф wkb = Vi04sin S © ’                    (18)

где фаза

^

S (^) = J VV (^') d^', а a0 – амплитуда волны.

Это ВКБ-решение недействительно вблизи точки сингулярности ξ S , где функция V ведет себя как

V =

a

IT-l⁷ ’

где a – положительная константа. В этой области ос- новное решение уравнения (17) записывается в виде

ФBes = ЛГ-1 X x [ av J 1 (2ТаПГ-!)) + a211 (2Т^ИГ"1))] ’ ( )

где J 1 и Y 1 – функции Бесселя. Сравнение этого решения с (18) дает константы a 1 и a 2 :

i n /4

a1 = a 0 Vne cos S 0, a2 = a0 Vne in/4 sin S0, где S0 = S (lS) - полное дополнение фазы волны между ионосферой и точкой сингулярности. Поле волны, определяемое уравнениями (18), (19), изображено на рис. 2.

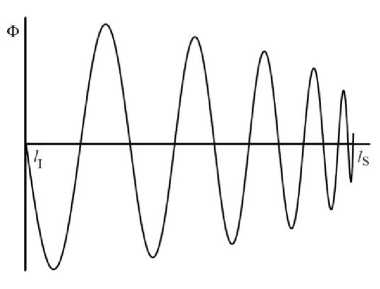
Рис . 2. Продольная структура волны в около-ионосферной области проводимости.

Главный член асимптотического вблизи точки сингулярности имеет вид разложения

Φ

Bes ⁼

= a ₀ π e ^{- i π /4} sin S ₀

α ( ξ S -ξ ) ln α ( ξ S -ξ ) -π

απ

Видно, что амплитуда волны вблизи точки сингулярности конечна.

Дисперсионное соотношение вдали от точки сингулярности имеет альфвеновскую форму kn≈ω/A, где A = B/ 4π(ρp +ρh ) . Таким образом, для первой гармоники ионосферного резонатора продольная компонента волнового вектора имеет вид кц ~

¹ +p h

V ^p p 7

ch

A

.

Для параметров плазмы, показанных в предыдущем разделе, получается длина волны λ=0.8 R E .

Заключение

Подведем итоги. Статья посвящена УНЧ-коле-баниям в космической плазме с примесью тяжелых ионов. Частота колебаний порядка гирочастоты тяжелых ионов (диапазон Рс1). Наибольший интерес в диапазоне (Ω_ch<ω<Ω_cp) представляют две непрозрачные области, формируемые по разные стороны от экватора. Эти области препятствуют распространению мод вдоль силовой линии в виде бегущей волны. В экваториальной области формируется резонатор. По каждую сторону от резонатора есть область непрозрачности, ограниченная точкой сингулярности, далее следует область прозрачности между этой точкой и ионосферой, в этой области образуется стоячая волна. В точке сингулярности величина продольного волнового вектора к ц большая, но амплитуда волны конечна.

Таким образом, мы приходим к следующей физической картине. Нестабильности в космической плазме возбуждают собственные моды экваториального резонатора, который служит резервуаром энергии. Часть волновой энергии утекает из резонатора. После туннелирования сквозь области непрозрачности и отражения волн от ионосферы формируется стоячая волна между ионосферой и точкой сингу- лярности. Частота волны определяется собственными частотами резонатора. Поскольку эти собственные частоты незначительно отличаются друг от друга, возбуждения многих гармоник могут в результате формировать биения, очень похожие на характерную структуру жемчужин. С другой стороны, более высокие собственные частоты в резонаторе могут образовать волновой пакет, способный перемещаться между точками отражения в резонаторе, как было показано в работах [Guglielmi et al., 2000, 2001; Guglielmi, Kangas, 2007; Гульельми, 2007; Lundin, Guglielmi, 2006]. Детальное изучение формирования повторяющейся структуры – предмет другого исследования, которое должно включать решение волнового уравнения с временной зависимостью.

Данная работа подтверждает результаты статей [Guglielmi et al., 2000, 2001; Гульельми, 2007], рассматривающих продольный резонатор для УНЧ-волн в мультикомпонентной плазме в экваториальной области. Следует заметить, что в названных статьях представлены случаи, отличные от нашего. Как уже было отмечено, волновые уравнения, рассматриваемые в работах, соответствуют дисперсионному соотношению (7) с отброшенным k _⊥ , т. е. было изучено продольное распространение. В данной статье рассматривается явление, аналогичное резонансу силовых линий, когда к _± ^ к ц . Добавим, что количественные характеристики экваториального резонатора (собственные частоты, ширина) в настоящей работе совпадают с теми, что указаны в вышеупомянутых статьях. Это подтверждает, что экваториальный резонатор не является абстрактным, возникающим из-за применения квазипродольного приближения, это реальная особенность УНЧ-волн в многоионной космической плазме.

Приведем пример квазипродольного приближения. В работе [Klimushkin, Mager, 2006] было обнаружено, что аксиально-симметричные колебания (азимутальное волновое число m =0) распространяются поперек магнитных оболочек, испытывая отражения от некоторых магнитных поверхностей. На такой поверхности обе поперечные компоненты волнового вектора равны нулю, что означает квазипродольное распространение. Таким образом, взаимно противоположные случаи к _± ^ к ц и к ц ^ к _± могут легко соответствовать волновой структуре в разных местоположениях на радиальной координате.

Результаты, полученные в данном исследовании, также могут быть применены к исследованиям УНЧ-волн в магнитосфере планеты Меркурий, где роль тяжелых ионов играет натрий [Othmer et al., 1999; Glassmeier et al., 2003, 2004].

Работа выполнена при поддержке программы Президиума Российской академии наук № 4, Отделения физических наук РАН № 15 и программы № 9 Отдел наук о Земле РАН.