Прикладная теория неупругости

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2018PNRPU MECHANICS BULLETIN

Вопросам построения прикладных вариантов теорий термовязкопластичности и неупругости посвящено большое количество работ. Основные направления построения теорий и обширную библиографию по этому вопросу можно найти в монографиях, обзорах и отдельных работах А.А. Ильюшина [1, 2], В.В. Новожилова [3], Ю.Н. Работнова [4], И.А. Биргера [5], В.С. Бондаря [6–9], Р.А. Васина [10], Ю.И. Кадашевича [3], Л.М. Качанова [11], Ю.Г. Коротких, И.А. Волкова и Л.А. Игумнова [12–15], Н.Н. Малинина [16], Ю.М. Темиса [17], Кремпла [18, 19], Криега [20–22], Леметри [23], Лин-хольма [24], Миллера [25–27], Оно [28–31], Харта [32], Шабоша [33–38] и др.

Наибольшее распространение в практических расчетах в настоящее время получили прикладные варианты теории течения, базирующиеся на концепции комбинированного упрочнения. Среди этих вариантов теорий теории В.С. Бондаря [6–9], Ю.Г. Коротких [12–15] и Шабоша [33–38] являются наиболее экспериментально обоснованными и широко применяемыми для расчетов ресурса материалов конструкций при термовязкопластическом деформировании в условиях повторности и длительности термомеханических воздействий. Следует отметить, что в вариантах теорий Ю.Г. Коротких и Ша-боша деформации разделяются на упругие, пластические и ползучести, а в варианте теории В.С. Бондаря – на упругие и неупругие. Поэтому первые варианты относятся к теории термовязкопластичности, а последний – к теории неупругости. Соответственно, и эволюционные уравнения для радиуса поверхности нагружения, смещений (микронапряжений) и накопления повреждений в первом случае строятся отдельно для пластичности и ползучести, а во втором случае – только для неупругости. Следует отметить, что разделение необратимой деформации на деформации пластичности и ползучести весьма условно. При быстрых процессах деформации ползучести малы и ими пренебрегают и говорят о пластическом деформировании, при медленных процессах имеют место и пластические деформации, и деформации ползучести, и разделение их весьма условно, т.е. в данном случае необратимая деформация едина. Разрушение при быстрых процессах деформирования обычно носит вязкий характер при накоплении повреждений в теле зерна, а при очень медленных процессах – хрупкий характер при накоплении повреждений по границам зерен. Поэтому в первых ва- риантах процессы накопления повреждений разделены и описываются разными кинетическими уравнениями. Основным недостатком первого подхода является отсутствие взаимного влияния процессов пластичности и ползучести как при деформировании, так и при разрушении, что противоречит экспериментальным результатам [4–6, 10–16]. Во втором случае история процесса деформирования и взаимовлияние пластичности и ползучести учитывается априори – быстрый процесс влияет на последующий медленный и наоборот. Что касается разрушения, то наличие в уравнениях теории кинетического уравнения, описывающего охрупчивание, дает возможность как вязкого (при значительных деформациях и кратковременных процессах или малом числе циклов), так и хрупкого (при небольших деформациях и больших длительностях процесса, а также при многоцикловой усталости) разрушения. Соответственно, этот вариант теории позволяет моделировать и смешанные виды деформирования, и разрушения.

Следует отметить некоторые особенности рассматриваемой здесь прикладной теории неупругости:

• –    деформация имеет упругую и неупругую составляющие (нет условного разделения на деформации пластичности и ползучести);

• –    поверхность нагружения может смещаться, расширяться, сужаться или иметь постоянный размер;

• –    нагружение, соответствующее движению по поверхности нагружения, не всегда является нейтральным (упругим);

• –    трехчленная структура уравнений для смещения поверхности нагружения обусловливает снятие ограничений на траектории сложного нагружения;

• –    кинетические уравнения накопления повреждений построены на энергетическом принципе с учетом процессов охрупчивания и залечивания и адекватно отражают нелинейные процессы накопления повреждений;

• –    уравнения неупругого поведения и накопления повреждений взаимосвязаны, т.е. повреждение влияет на поведение, а история нагружения на процесс повреждения;

• –    основу метода идентификации материальных функций составляет обработка кривых базового эксперимента, не связанная с определением пределов текучести и других величин с какими-либо допусками;

  – базовыми экспериментами, на которых построен метод идентификации материальных функций, являются стандартные испытания материала на малоцикловую и длительную прочность, а также деформирование в условиях пластичности и ползучести.

В настоящей работе рассматриваются основные положения и уравнения прикладной теории неупругости, относящейся к классу теорий течения при комбинированном упрочнении. Выделяются материальные функции, замыкающие прикладную теорию неупругости, формулируется базовый эксперимент и метод идентификации материальных функций. Рассматривается пример определения материальных функций по результа-

там базового эксперимента, и приводятся материальные функции для нержавеющей стали 12Х18H9 в диапазоне температур от 20 до 650 °С. Дается перечень экспериментов и конструкционных сталей и сплавов, на которых была проведена верификация прикладной теории неупругости в условиях пластического и термовязкопластического деформирования, изотермического и неизотермического, простого и сложного нагружения.

1. Основные положения и уравнения

Материал однороден и начально изотропен. Рассматриваются малые деформации поликристаллических конструкционных сталей и сплавов при температурах, когда нет фазовых превращений, и скоростях деформаций, когда динамическими эффектами можно пренебречь. В процессе неупругого деформирования в материале может возникать только деформационная анизотропия. Тензор скоростей деформаций представляется в виде суммы тензоров скоростей упругой и неупругой деформаций:

8 j = 8 j +8 H . (1)

Следует отметить, что здесь нет условного разделения неупругой деформации на деформации пластичности и ползучести.

Упругие деформации при изменении напряжений следуют обобщенному закону Гука, а при изменении температуры – закону температурного расширения. Тогда с учетом зависимости упругих параметров от температуры упругие деформации будут определяться следующим образом:

8j = 1 [aj -v(3^05j -aj)] + a8TT ’

aj = aT5j --^[aj -v(3a5j -aj)]x

dE x-- dT

-1 ( 3ao 5 j

-a

J dv. ij ) dT

где E, v , a_T - соответственно модуль Юнга, коэффициент Пуассона, коэффициент температурного расширения, являющиеся функциями температуры T ; a₀ = a_zz / 3 -среднее напряжение; 5 ij - символ Кронекера ( 5 ij =1 при i = j ; ⁵ j = ⁰ при i * j ).

Полагается, что в пространстве составляющих тензора напряжений существует поверхность нагружения, разделяющая области упругого и неупругого состояний. Поверхность нагружения изотропно расширяется или сужается и смещается в процессе нагружения. Начальная поверхность нагружения может быть стянута в точку. Текущая поверхность нагружения определяется процессом нагружения. Воздействие фактора времени тоже есть процесс нагружения. Уравнение поверхности нагружения принимается в следующем виде:

f ^(o j ) = ^{3 (} s j - °_х s j - " 9- C ²= °-        ⁽³⁾

Здесь s _z* = s_y - a_y - девиатор активных напряжений [3]; s_ij – девиатор напряжений; тензор a_ij (добавочных напряжений, остаточных микронапряжений [3,5]) характеризует смещение поверхности нагружения в деви-аторном пространстве напряжений, т.е. направленное (анизотропное) упрочнение. Скаляр C отвечает размеру (радиусу) поверхности нагружения и характеризует изотропное упрочнение. Тензор смещения a_ij и радиус C являются функционалами процесса нагружения.

Для радиуса поверхности нагружения принимается следующее уравнение:

C = q _£ ^£ и * ⁺ q T ^T - q R .                 ⁽⁴⁾

Здесь £ H* - длина дуги траектории неупругой деформации (накопленная неупругая деформация); £ н* - интенсивность скоростей неупругой деформации (скорость накопленной неупругой деформации); q_£, q_T, q_R -функции, подлежащие экспериментальному определению. Первое слагаемое в уравнении (4) отвечает механическому упрочнению. По знаку q определяются циклически упрочняющиеся ( q >0), стабильные ( q = 0) и разупрочняющиеся ( q <0) материалы. Параметр q обеспечивает неизотермический переход, а параметр q – возврат механических свойств при отдыхе, отжиге.

Смещение поверхности нагружения определяется уравнением

.      2   . Г 2 и

Cl- — — PE • • + — P" £ ■ ■ + P" Cl • • £ * + j 3 g ij \ 3 g £ ij g^a ij I и *

+ Г 3 g Т £ н + g T j T -Г 3 g R £ н + g R a  -     (5)

Здесь g, g £ , g_a , g T , g T , g^R, g^R - функции, подлежащие экспериментальному определению. Первые три слагаемых в уравнении (5) описывают процессы образования и снятия добавочных напряжений при неупругом деформировании, два следующих обеспечивают неизотермический переход, а два последних – снятие добавочных напряжений при отдыхе, отжиге. Параметры q_R, g^R, g^R в уравнениях (4) и (5) являются функциями повреждения, что позволяет описать разупрочнение материала перед разрушением, т.е., например, уменьшение уровня напряжений при жестком циклическом нагружении перед разрушением, третью стадию ползучести.

Зависимость параметра q в уравнении (4) от меры непропорциональности (сложности) нагружения позволяет [7–9, 39] описать эффект дополнительного изо-

тропного упрочнения при непропорциональных циклических нагружениях, который имеет место для ряда конструкционных материалов – нержавеющих сталей.

Неупругие деформации зависят от истории нагружения и являются функционалами процесса. Для определения скоростей неупругих деформаций используется ассоциированный с (3) градиентальный закон течения

о ^н₌ jf_ I ₌ ³ sj н«

^£ ij          ^ _n *   ^£ u * .

So j    ² о „

Здесь о * - интенсивность активных напряжений.

Для получения уравнения для скорости накопленной неупругой деформации используются уравнения (1)–(6). Тогда для случаев мягкого и, соответственно, жесткого нагружений уравнения для скорости накопленной неупругой деформации будут иметь следующий вид:

н

^£ и *

£н* и *

E *

*  .

jj - b^tT + b^r _ *

и

,

E. + 3G *

*   *

s.. £         _ .        _

3 G^-^ i- - B T T + B^R

*

_ н*  .           *

^E * = q £ ⁺ g ⁺ g ₆ ^£ и ⁺ g a ^a u ,

B^T = q T + g T £ Г+ g T a U , B R = q R + g R £ н * + g R a * ,

* H

S : £

н * У ___У_

^£ u        *

^o u

.   3 s j a j

, a„=^ —

^{2 o} u

-

² ( 1 + v )

Условия упругого и неупругого состояний следуют из того, что для неупругого состояния необходимо, чтобы изображающая точка процесса нагружения находилась на поверхности нагружения и определяемая скорость накопленной неупругой деформации была положительна, а упругое состояние следует при нарушении любого из двух упомянутых условий. Тогда условия упругого и неупругого состояний будут иметь следующий вид:

oU < Cu £н*< °  - упругость, oU = C п £н* > °  - неупругость.

Здесь под £ н * подразумевается выражение, задаваемое уравнением (7) либо (8) или любым другим уравнением, связывающим скорость накопленной неупругой деформации и любой набор скоростей напряжений и деформаций (смешанное нагружение).

Для описания процесса накопления повреждений используется энергетический подход. В качестве энергии, расходуемой на создание повреждений в материале, принимается энергия, равная работе добавочных напряжений на поле неупругих деформаций. Ответственность за накопление повреждений добавочных

напряжений (микронапряжений) иллюстрируется результатами, приведенными в работах [40–43]. В процессе нагружения имеют место: накопление повреждений за счет работы добавочных напряжений (микронапряжений), залечивание повреждений и охрупчивание материала. Залечивание и охрупчивание связаны с длительностью процесса нагружения. Кинетические уравнения накопления повреждений, залечивания и охрупчивания принимаются в следующем виде:

.     — a^Лн ю = аго“ -^7-- gЮю,             (10)

W

W = g W T — g w W .              (11)

Здесь го - мера повреждения ( юе [ 0;1 ] ) ; W - энергия разрушения; a , g _го , g W , g_w - функции, подлежащие экспериментальному определению. Функция а описывает [42, 43] нелинейность процесса накопления повреждений. Первое слагаемое в уравнении (10) описывает процесс накопления повреждений за счет работы добавочных напряжений на поле неупругих деформаций. Второе слагаемое в уравнении (10) описывает процесс залечивания повреждений, интенсивность которого зависит от уровня повреждения, а также от уровня и характера напряженного состояния. Первое слагаемое в уравнении (11) обеспечивает неизотермический переход. Второе слагаемое в уравнении (11) описывает изменение энергии разрушения (начальная энергия разрушения равна W и определяется при пластическом деформировании) за счет процесса охрупчивания материала, интенсивность которого зависит от текущего значения энергии разрушения и уровня напряженного состояния. Критерием разрушения материала будет достижение повреждением предельного значения, обычно принимаемого равным или близким к единице.

• 2.    Материальные функции

Теорию неупругости замыкают следующие материальные функции:

E ( T ) , v ( T ) , а_г ( T ) - упругие параметры;

Ea (T), с a (T), Р( T)   - модули анизотропного упрочнения;

C ( T , £ И* ) - функция изотропного упрочнения;

W ( T ) - начальная энергия разрушения;

b c ( ^T ) , b a ( ^T ) , n c ( ^T ) , n a ( ^T ) , m ro ( ^T ) ^- параметры изотропной и анизотропной ползучести;

b x ( T ) , b p ( ^T ) , n x ( ^T ) , n p ( ^T ) ^- параметры залечивания и охрупчивания.

Определяющие функции выражаются через материальные следующим образом:

дCp       C дCp q£   д£н. , qT   Cp dT qR = q e Pc,

g = E a +P ^C a , g £ =P ^E a , g a = ^- P ,

, T _ ^dE a   ^dE a ^{d C} a    T ₌ 1 d ^C a

£ dT   a„ dT ’ ga с dT ’ gR = g£Pa , gR =(g + gaau ) Pa",

a

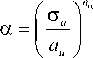
g ro = ^X , g w = P , g W =

W dW

W dT ^,

P c = exp ( b c ) C - C_p о| n c ( 1 -ro )^- m " ,

P , = exp ( b_a )( a_u ) n^a ( 1 -ro )^- m ^ro ,

'0,                 если с_и >  0,

_ exp ( ^bx ) |c ii l " ^X , ^если с ц <  0,

P = ^exp ( b p ) ( ^c и ) n ^P ,

a

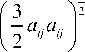
^с и

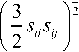
C p о = C p ( T ,0 ) = с _ 1 .

Здесь c_j - предел длительной прочности (предел ползучести); n – параметр нелинейности процесса накопления повреждений ( n_a = 1,5 ) . Следует отметить, что при несимметричных циклических нагружениях имеет место посадка или вышагивание петли пластического гистерезиса. Для описания этих явлений модуль E принимается [42-45] зависящим от £ н* .

Ниже рассматриваются возможности вариантов теории неупругости и требуемое число материальных функций.

Изотермическое нагружение

E, V , Е_а , с _а , в , C p (_Е и . )

E, V , E a , с _а , в , C p ( £ н . ) , W o

пластичность

(6 параметров)

пластичность + разрушение

(7 параметров)

Е , v , Е , о , В , С (е " ,), b , n ,  , a , a , г, p\ и * p a , a

пластичность + установившаяся ползучесть (8 параметров)

Е , v , Е , ° , В , С ( е " ,) , b , b , n , n a  a     p  и    ca  c  a

пластичность + первая и вторая стадии ползучести (10 параметров)

Е , V , E a , ° a , P , C p ( E " . ) , W 0 , b a , n a , m Ш

пластичность + вторая и третья стадии ползучести + разру шение без учета охрупчивания и залечивания (10 параметров)

Е , V , E a , ° a , P , C p ( E " * ) , W 0 , b a , n a , m Ш , b p , n p

пластичность + вторая и третья стадии ползучести + разру шение с учетом охрупчивания, но без залечивания (12 параметров)

Неизотермическое нагружение

Е ( T ) , v ( T ) , a t ( T ) E a ( T ) , ° a ( T ) , P ( T ) , C p ( T , е " . ) , W o ( T ) b a ( T ) , n a ( T ) , m m( T ) , b p ( T ) , n p ( T )

пластичность + вторая и третья стадии ползучести + разру шение с учетом охрупчивания, но без залечивания (13 параметров)

Е ( T ) , v ( T ) , a t ( T ) Еа ( T ) , ° a ( T ) , P ( T ) , C p ( T , е "  * ) , W o ( T ) b c ( T ) , b a ( T ) , n c ( T ) , na ( T ) , m m( T ) b , ( T ) , b p ( T ) , n x( T ) , n p ( T )

пластичность + первая, вторая и третья стадии ползучести + разрушение с учетом охрупчивания и залечивания (17 параметров)

• 3.    Базовый эксперимент

Для определения материальных функций достаточно следующего основного (базового) набора экспериментальных данных при различных уровнях температуры:

• -    упругие параметры Е, v , а_т , которые определяются традиционными методами;

• –    диаграмма пластического деформирования при одноосном растяжении о, ( е ) до деформации 0,05-0,1;

• –    диаграмма пластического деформирования при одноосном растяжении °₂ ( е ) до деформации 0,05-0,1 после предварительного сжатия до деформации 0,01–0,02;

• –    данные по циклическому одноосному растяжению-сжатию (знакопеременному кручению) при постоянном размахе пластической деформации: число циклов до разрушения (появления макротрещины) N_p и зависимость максимальных значений напряжений □ + на цикле (в конце цикла) от числа циклов нагружения N (размах пластической деформации Ае ^н порядка 0,01-0,02);

• –    данные по ползучести при постоянном напряжении растяжения: зависимость минимальной скорости ползучести от напряжения во всем диапазоне изменения напряжений от кратковременной до весьма длительной ползучести;

• –    данные по длительной прочности: кривая длительной прочности при растяжении, включающая все

• 4.    Пример определения материальных функций

  Для определения параметров анизотропного упрочнения Е_а, в , °_а и функции изотропного упрочнения С р (е^ ) при начальных значениях накопленной неупругой деформации необходимы диаграммы растяжения и растяжения после предварительного сжатия в условиях пластичности. На рис. 1 приведены диаграммы растяжения о, и растяжения °₂ после предварительного сжатия до деформации |ен₂ | =0,0166 как функции накопленной неупругой деформации. Далее, используя данные на рис. 1, строим кривую (рис. 2) в координатах

три участка, и кривая длительной прочности при сжатии, соответствующая только второму участку.

у = °ТТ^, x = ^е н* -И^{,         (14)}

• ² |^е02|

горизонтальной асимптотой которой является прямая у = Е_а , что позволяет определить значение параметра Е .

Для получения параметров р и °, зависимости на рис. 2 перестраиваются в координатах z = In

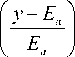
x = 8H* -

| ен2|

Рис. 3. Определение параметров ст_о и в

Fig. 3. Determining ст_а and в parameters

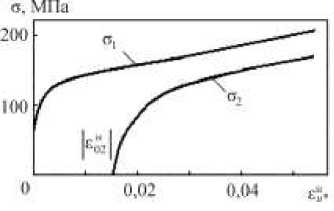
Рис. 1. Кривые растяжения и растяжения после предварительного сжатия Fig.1. Curves of stretching and stretching after prior compression

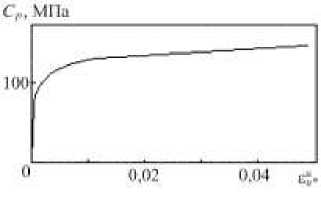
Рис. 4. Функция изотропного упрочнения

Fig. 4. Isotropic hardening function

t. МПа

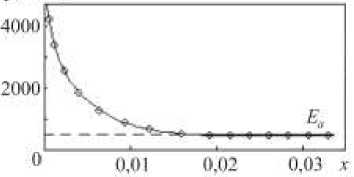
Рис. 2. Определение параметра E

Fig. 2. Determination of E parameter

Для остальных значений накопленной неупругой деформации функция изотропного упрочнения определяется по результатам циклических испытаний (табл. 1) при постоянном размахе неупругой деформации Ае ^н = = 0,015 и деформации на первом полуцикле е н =

= 0,0075 по формуле

Cp (еи* ) = СTN   Ea |е02| СТa

1 - exp (-вАен)

1 + exp (-вАен)

Получаемая с помощью метода наименьших квадратов линейная зависимость (рис. 3) позволяет по углу наклона ф и ординате z₀ определить параметры в и ст_а по формулам

ен* =|ен2| + 2Аен N.

Таблица 1

Максимальные значения напряжения на N -м цикле

Table 1

_n               E a Е02 exP ( ^z о )

в = tgф , СТ a =                   .

1 - exp (-Р Бо2 )

Maximum stress values of N- th cycle

N , цикл	3	5	15	30
ст + , МПа	232	242	250	252

Примечание: СТ + - максимальные значения напряжения на N -м цикле, N – номер цикла. Первый цикл включает в себя второй и третий полуциклы и т.д. Первый же полуцикл обычно называется отнулевым циклом.

Получив параметры анизотропного упрочнения Е_а, р , ст_а , можно определить функцию изотропного упрочнения С_р ( ен, ) , используя диаграмму растяжения, по формуле

На рис. 5 приведена кривая зависимости С_р ( ен, ) ,

Cp (ен*) = ст, (ен*) - Eaен. -стa [1 - exp (-вен.)] .  (17)

полученная на основе формул (17) и (18).

На рис. 4 показана кривая зависимости С_р ( ен, ) , полученная на основе формулы (17).

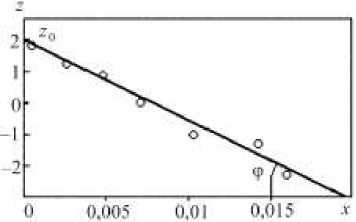
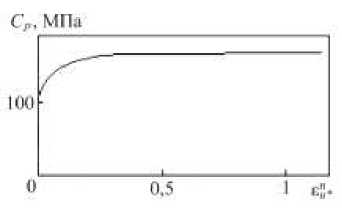
Рис. 5. Функция изотропного упрочнения

Fig. 5. Isotropic hardening function

Далее по результатам циклических испытаний до разрушения в условиях пластичности с постоянным размахом неупругой деформации определяется энергия разрушения W по формуле

2a . „

W o =у V -²

1 - exp ( -рДе н )

1 + exp ( -рДе н )

N p .     (19)

Здесь Де н - размах неупругой деформации, а N p - число циклов до разрушения, которые в данном случае соответственно равны 0,015 и 44.

Таким образом, для каждого уровня температуры Т определяются материальные функции (параметры), соответствующие упругопластическому состоянию:

E ( T ) ; v ( T ) ; а _т ( T ) ; E , ( T ) ; а a ( T ) ; р ( T ) ;

C_p ( T , е Н* ) , W ( T ) .

Далее определяются материальные функции, отвечающие за временные эффекты по результатам испытаний в условиях ползучести.

Для определения параметра изотропной и анизотропной ползучести m используются данные первого и второго участков кривой длительной прочности, а также определенные ранее материальные функции, соответствующие пластическому состоянию. Параметр m определяется из линейной зависимости

У = (mm+ 1) x,(20)

где

У = lg[tp (а)m / D], x = lg(1 -Mi),

® ! = 2- {^{1 E} a ( ^e “ ) ^{2 + а} a ^е н - ^ [ 1 - exP ( ^- ₽ ^£ “ ) ]} . (22)

Wo 12                    PJ

Здесь tp – время до разрушения в условиях кратковременной ползучести при напряжении а; ен - пластическая деформация, соответствующая напряжению а; D, m – коэффициенты степенной аппроксимации второго участка кривой длительной прочности, tp = Dа"m.                    (23)

Значения коэффициентов степенной аппроксимации в данном случае соответственно D = 10 ^21,5 , m = 9 .

В табл. 2 приведены значения времени до разрушения для различных значений напряжения, соответствующих первому участку кривой длительной прочности.

Таблица 2

Длительная прочность на первом участке

Table 2

Long-term hardening at the first section

а , МПа	280	260	240	200
t p , ч	0,059	0,157	0,432	3,850

На рис. 6 приведена линейная зависимость (25), построенная на основе метода наименьших квадратов.

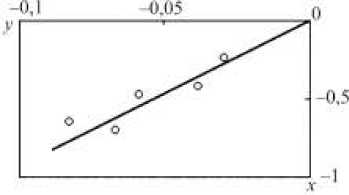
Рис. 6. Определение параметра m

Fig. 6. Determining m parameter

Далее, используя экспериментальные данные второго участка кривой длительной прочности и данные по скорости установившейся ползучести, параметры анизотропной ползучести b и n можно определить по формулам

n

ne m - n£

b a = ln

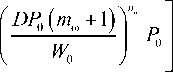
Здесь P, n – коэффициенты степенной аппроксимации зависимости установившейся скорости ползучести от напряжения e^t = Po (а)ne,                      (26)

в данном случае P_o = exp ( - 35,46 ) , n_£ = 6 .

Для определения параметров изотропной ползучести b и n используются данные зависимости установившейся скорости ползучести eНt от напряжения а. Вначале для набора значений напряжений, в данном случае для ае[80;140], по формуле (26) определяется соответствующий набор значений скорости установившейся ползучести. Затем на основании формулы a = [ен /eXP (ba )]na                 (2Т)

вычисляются соответствующие значения добавочного напряжения и соответствующие значения радиуса поверхности нагружения по формуле

C = а- a .                  (28)

Таким образом, устанавливается соответствие между н скоростью установившейся ползучести еst и радиусом С . Далее, представляя эту зависимость в координатах

У = 1п е ^ t , x = ln| C - C p o| ,             (29)

можно получить параметры b и n из линейной зависимости y = Ьс + ncx ,                    (30)

которая представлена на рис. 7.

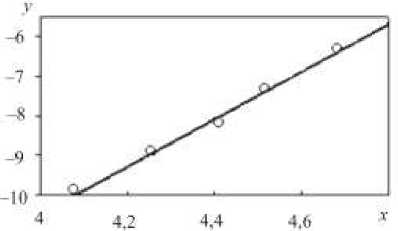
Рис. 7. Определение параметров Ь_с и n_c

Fig. 7. Determining Ь_с and n_c parameters

Для определения параметров охрупчивания Ь _р и n _р используются результаты испытаний, относящиеся к третьему участку кривой длительной прочности. В табл. 3 приведены значения времени до разрушения для разных значений напряжения, соответствующих третьему участку кривой длительной прочности.

Таблица 3

Длительная прочность на третьем участке

Table 3

Long-term hardening at the third section

ст , МПа	100	80	60
t p , ч	950	3550	17 000

Значение модуля охрупчивания р определяется для каждого уровня напряжения из следующего нелинейного уравнения:

р = -1ln [ 1 + р D ( ст ) ^-" ] .              (31)

tp

Решение нелинейного уравнения (31) осуществляется любым итерационным методом. В качестве начального приближения можно принять

Р = 7.(32)

tp

Далее, представляя зависимость между р и ст в логарифмических координатах y = lnр , x = lnст,(33)

можно получить параметры Ь _р и n _р из линейной зависимости

У = Ьр+ nрx,(34)

которая представлена на рис 8.

Для определения параметров залечивания b и n используются данные по длительной прочности при растяжении и сжатии, относящиеся ко второму участку кривых длительной прочности. Вначале для набора значений напряжений, в данном случае для ст е [150; 200], по формулам t> D + (ст)-", t- = D-Н’"          (35)

определяются соответствующие значения t + при растяжении и t ^- при сжатии. Затем значение модуля залечивания X определяется для каждого уровня напряжения из следующего нелинейного уравнения:

^х = “r f ^{1 - e}xP ( ^-X t - ) ] .              (36)

tp

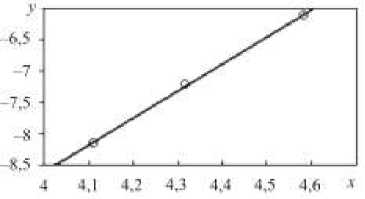
Рис. 8. Определение параметров b и n

Fig. 8. Determining Ь _р and n parameters

Решение нелинейного уравнения (36) осуществляется любыми итерационными методами. В качестве начального приближения можно принять

^X = 7

tp

t -

Далее, представляя зависимость между X и |ст| в логарифмических координатах y = lnX, x = ln|ст|,                   (38)

можно получить параметры b и n из линейной зависимости y = Ьх+ nxx,                    (39)

которая представлена на рис. 9.

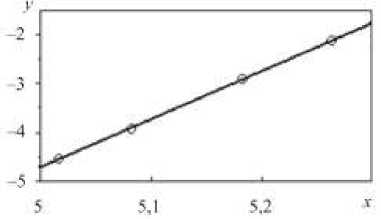
Рис. 9. Определение параметров b и n

Fig. 9. Determining b and n parameters

Следует отметить, что представленный алгоритм получения параметров залечивания приводит к верному решению в том случае, если время разрушения при растяжении незначительно отличается от времени разрушения при сжатии. Поэтому для уточнения параметра залечивания b проводятся расчеты длительной прочности при сжатии и корректировка b до совпадения расчетных и экспериментальных результатов.

На основе приведенного выше метода и примера идентификации материальных функций были получены материальные функции для нержавеющей стали 12Х18Н9 в диапазоне температур от 20 до 650 °С на основе экспериментальных данных [54–56]. В табл. 4, 5, 6 приведены материальные функции стали 12Х18Н9 (табл. 5 - функция изотропного упрочнения C_p ( T , e“. ) ). Данные в таблицах соответствуют температуре, задаваемой в °С; напряжениям, задаваемым в МПа; времени, задаваемому в часах.

Таблица 4

Упругие параметры. Модули анизотропного упрочнения, начальная энергия разрушения

Table 4

Elastic parameters. Anisotropic hardening modules, initial energy of destruction

Т , °С	Е , МПа	ν	α Т , 1/град	Е а , МПа	σ а , МПа	β	W 0 , дж/см3
20	205 000	0,3	1,69·10–5	500	150	500	270
150	195 000	0,3	1,77·10–5	200	124	500	200
300	182 500	0,3	1,87·10–5	50	117	500	150
500	167 000	0,3	2·10–5	0	96	500	88
550	163 000	0,3	2,03·10–5	0	88	500	72
600	159 000	0,3	2,06·10–5	0	76	500	56
650	155 000	0,3	2,08·10–5	0	60	500	40

Таблица 5

Функция изотропного упрочнения

Table 5

Anisotropic hardening function

Т , °С	н u *
	0	0,0005	0,002	0,005	0,01	0,02	0,04	0,1	0,4	100
20	10	190	218	225	228	236	254	300	310	320
150	10	150	179	189	192	200	220	266	276	286
300	10	130	165	180	184	194	214	260	270	280
500	10	100	124	133	136	146	166	212	222	232
550	10	93	118	127	132	142	160	200	210	219
600	10	86	112	121	128	138	154	190	198	206
650	10	80	107	116	125	134	148	180	188	194

Таблица 6

Параметры изотропной и анизотропной ползучести, залечивания и охрупчивания

Table 6

Isotropic and anisotropic creep, healing and brittling

Т , °С

m m

bc

nc

ba

na

b p

n p

b X

n X

20	7	–60,4	6	–27	2	–51	4	–92,6	9
150	7	–54,4	6	–22	2	–45	4	–80,6	9
300	7	–48,4	6	–17	2	–39	4	–68	9
500	7	–40,4	6	–13,06	2	–31.5	4	–57,5	9
550	7	–38,4	6	–12,21	2	–29	4	–54,94	9
600	7	–36,4	6	–11,48	2	–26.9	4	–52,29	9
650	7	–34,4	6	–10,93	2	–24.8	4	–49,7	9

• 5.    Перечень экспериментов и конструкционных материалов, на которых была проведена верификация теории

Пластичность

Изотермическое нагружение

Простое нагружение

Циклическое нагружение

Вид нагружения	Материал	Эксперимент
Cтационарное жесткое циклическое одноосное растяжение-сжатие, Т = 150 °С	АЛ-25 – циклически разупрочняющийся материал	Е.А. Аверченков и др. [46]
Жесткое нестационарное циклическое одноосное растяжение-сжатие. Блочное изменение амплитуды и асимметрии цикла, Т = 20 °С	12Х18Н10Т – циклически стабилизирующийся материал	Д.А. Казаков В.С. Бондарь [6]
Жесткое стационарное циклическое однооосное растяжение-сжатие. Усталостное разрушение от 103 до 105 циклов, Т = 20 °С	AISI 304 – циклически стабилизирующийся материал	D. Socie [47]
Жесткое стационарное цикличеcкое одноосное растяжение-сжатие. Усталостное разрушение от 2·10 до 2·104 циклов, Т = 20 °С	12Х18Н9 – циклически стабилизирующийся материал	Д.А. Казаков В.С. Бондарь [6]

Сложное нагружение

Плоские траектории

Вид нагружения	Материал	Эксперимент
Двузвенные ломаные траектории деформаций. Угол излома траектории от 15 до 100°. Длина первого звена от 0,002 до 0,0145. Т = 20 °С, P , q – опыты.	30ХГСА	В.П. Дегтярев [48]
Двузвенные ломаные траектории напряжений. Угол излома траектории от 130 до 180°, Т = 20 °С, Р , М – опыты	Ст 10	О.А. Шишмарев [49]
Двузвенные ломаные траектории деформаций. Угол излома траектории от 30 до 180°, Т = 20 °С, Р , М – опыты.	S15C	Y. Ohashi [50]
Двузвенные ломаные траектории напряжений. Угол излома траектории 90°, Т = 20 °С, Р , М – опыты.	30ХГСА	А.С. Вавакин и др. [51]
Трехзвенные ломаные траектории деформаций. Угол первого излома 90°, угол второго излома 60, 70, 80°, Т = 20 °С, Р , М – опыты.	S10C	Y. Ohashi [50]
Криволинейные траектории деформаций: луч+дуга окружности, Т = 20 °С, P , q – опыты.	30ХГСА	В.П. Дегтярев [48]
Криволинейные траектории деформаций: луч + дуга окружности + луч + дуга окружности + луч. Т = 20 °С. Р , М – опыты.	BsBM2	Y. Ohashi [50]
Траектория деформаций в виде квадрата, 3 витка, Т = 20 °С, Р , М – опыты.	40Х16Н9Г2С	В.Г. Зубчанинов, Н.Л. Охлопков [52]
Траектория деформаций в виде окружностей с общим центром в начале координат. Радиус от 0,0025 до 0,0125, Т = 20 °С, Р , М – опыты.	40Х16Н9Г2С	В.Г. Зубчанинов, Н.Л. Охлопков [52]
Траектория деформаций в виде окружностей, проходящих через начало координат. Радиус от 0,0025 до 0,01, Т = 20 °С, Р , М – опыты.	9Х2	В.Г. Зубчанинов, Н.Л. Охлопков [52]
Траектория деформаций в виде спирали Архимеда. Скручивание в начало координат за 4 витка, а затем раскручивание 2 витка.	Ст. 45	В.Г. Зубчанинов, Н.Л. Охлопков [52]
Стационарные циклические нагружения по траекториям деформаций в виде двойного квадрата, квадрата, окружности. Усталостное разрушение от 4·103 до 2·105 циклов, Т = 20 °С. Р , М – опыты.	AISI 304	D. Socie [47]

Пространственные траектории

Вид нагружения                      ~I         Материал         I        Эксперимент

Траектории деформаций в виде винтовых линий с постоянной кривизной и кручением. Кривизна от 100 до 333 и крутка от 10 до 666. Всего восемь траекторий, Т = 20 °С, Р , М , q – опыты.

Cт. 45

А.С. Вавакин и др. [53]

Неупругость

Изотермическое нагружение

Простое нагружение

Вид нагружения	Материал	Эксперимент
Жесткое стационарное циклическое одноосное растяжение-сжатие, ε =10–4 1/c, Т = 250 и 350 °С	Ал – 25 – циклически разупрочняющийся материал	Аверченко [46]
Жесткое стационарное циклическое одноосное растяжение-сжатие, Т = 650 °С, длительность цикла 2 и 8 мин Усталостное разрушение от 102 до 10циклов.	12Х18Н9	А.П. Гусенков [54]
Длительная прочность при постоянном напряжении растяжения. Время разрушения от 0,1 до 103 ч. Т = 550, 600, 650 °С.	12Х18Н9	А.П. Гусенков [54]
Длительная прочность при постоянном напряжении растяжения. Время разрушения от 10 до 105 ч. Т = 550, 600, 650 °С	М3	В.В. Кашелкин С.А. Шестериков
Знакопеременная циклическая ползучесть. Длительность выдержки на режиме растяжения (сжатия) составляла 8 ч. Т = 650 °С, 5 циклов	AISI 304	Y. Ohashi [57]

Сложное нагружение

Вид нагружения	Материал	Эксперимент
Ползучесть при изломе траектории напряжений на угол 30, 90, 150°. Длительность выдержки в конце каждого луча напряжений составляла 8 ч, Т = 650 °С, 5 циклов	AISI 304	Y. Ohashi [57]
Двузвенные ломаные траектории деформаций, Т = 550 °С. ε = 5·10–4 мин–1, угол излома 60°. Длина первого звена 0,0025, 0,004, 0,0096.	30ХГСА	В.П. Дегтярев [48]
Двузвенные ломаные траектории деформаций, Т = 550 °С. ε = 5·10–4 мин–1. Угол излома 15, 42, 70°. Длина первого звена 0,006	30ХГСА	В.П. Дегтярев [48]
Двузвенные ломаные траектории деформаций, Т = 550 °С. Угол излома 60°. Длина первого звена 0,0055. ε = 5·10–3, 5·10–4, 1,65·10–4, 5·10–5 мин–1	30ХГСА	В.П. Дегтярев [48]

Неизотермическое нагружение

Простое нагружение

Вид нагружения	Материал	Эксперимент
Стационарное жесткое циклическое одноосное растяжение-сжатие. Противофазный режим изменения температуры и силовой деформации, Т = 150 ↔ 300 °С. Длительность цикла 180 с. 6 циклов нагружения.	Ал – 25 – циклически разуп-рочняющийся материал	Е.А. Аверченков и др. [46]
Стационарное жесткое циклическое одноосное растяжение-сжатие. Синфазный режим изменения температуры и деформации. Два режима: Т = 200 ↔ 375 °С, 185 ↔ 385 °С. Длительность цикла 95 с и 115 с. Усталостное разрушение	Ал – 25 – циклически разупрочняющийся материал	В.П. Белов В.С. Бондарь [6]

Сложное нагружение

Вид нагружения	Материал	Эксперимент
Малоцикловая прочность конических оболочек, подкрепленных кольцом жесткости на широком срезе, при теплосменах. Существенный знакопеременный градиент температуры по образующей на участке перехода от гладкой оболочки к кольцу жесткости. Реализуется сложное неизотермическое нагружение. Т = –115 ↔ 830 °С на гладкой оболочке и Т = –50 ↔ 600 °С на кольце жесткости. Длительности цикла 300 с.	ВЖ-100	Я.Г. Осадчий В.С. Бондарь [6]

Заключение

Наибольшее экспериментальное обоснование теория получила в области изотермического упругопластического деформирования. Здесь рассматривались достаточно произвольные процессы простого (циклического) нагружения, а также сложного нагружения как по плоским, так и по пространственным траекториям деформаций в достаточно широком диапазоне углов излома, кривизны и кручения траекторий. Рассматривались также циклические процессы сложного нагружения. Особо следует отметить, что развитие прикладной теории позволило описать эффекты дополнительного изотропного упрочнения при непропорциональных циклических нагружениях. Рассматривалось также разрушение материалов при циклических пропорциональных (простых) и непропорциональных (сложных) нагружениях. Все упомянутые выше процессы нагружения относятся к жестким режимам нагружения, т.е. нагружение осуществлялось по траекториям деформаций. Мягкие нагружения, которые осуществляются по траекториям напряжений, в должной мере не рассматривались. Однако в настоящее время развивается прикладная теория для описания процессов посадки и вышагивания петли пластического гистерезиса при несимметричных жестких и мягких циклических нагружениях.

Что касается области неизотермического упругопластического деформирования, то в диапазоне температур, при которых малы эффекты, связанные с длительностью процесса нагружения, никаких особенно