Прикладные методы математического моделирования финансово-хозяйственной деятельности предприятия (оптимизация остаточной прибыли, остаточного дохода предприятия, денежных доходов работников)

Доходами предприятий признается увеличение экономических выгод в результате поступления активов (денежных средств, иного имущества) и погашения обязательств, приводящее к увеличению капитала, за исключением вкладов участников (собственников имущества).

Не относятся к доходам предприятия такие поступления от других юридических лиц и граждан, как:

• 1)    сумма налога на добавленную стоимость, акцизы, экспортные пошлины и иные аналогичные обязательные платежи;

• 2)    оплата по договорам комиссии, агентским и другим аналогичным договорам в пользу комитента, принципала и др.;

• 3)    предварительная оплата продукции, товаров, работ и услуг;

• 4)    авансы в счет оплаты продукции, товаров, работ и услуг;

• 5)    залог, если договором предусмотрена передача заложенного имущества залогодержателю;

• 6)    погашение кредита, займа, предоставленного заемщику.

Доходы предприятия исходя из характера, условия получения и направлений деятельности классифицируются следующим образом:

• 1)    доходы от обычных видов деятельности;

• 2)    операционные доходы;

• 3)    внереализационные доходы;

• 4)    чрезвычайные доходы.

Доходы, отличные от доходов, получаемых от обычных видов деятельности, считаются прочими поступлениями. Прочие поступления (операционные, внереализационные и чрезвычайные доходы) подлежат зачислению на счет прибылей и убытков (счет № 80).

Доходом от обычных видов деятельности является выручка от реализации продукции и товаров, а также поступления от выполнения работ и оказания услуг.

В организациях, предметом деятельности которых является предоставление за плату во временное пользование своих активов по договору аренды, выручкой считаются поступления, получение которых связано с этой деятельностью (арендная плата).

В организациях, предметом деятельности которых служит предоставление за плату прав, возникающих из патентов на изобретения, промышленные образцы и других видов интеллектуальной собственности, выручкой считаются поступления (доходы) от данной деятельности. В организациях, предметом деятельности которых является участие в уставных капиталах других предприятий, выручкой считаются поступления, получение которых связано с этой деятельностью.

В бухгалтерском учете выручка отражается в сумме, определенной в денежном выражении, равной величине поступления денежных средств и иного имущества, а также величине дебиторской задолженности. Если величина поступления покрывает лишь часть выручки, то выручка, принимаемая к бухгалтерскому учету, исчисляется как сумма поступления и дебиторской задолженности (в части, не покрытой поступлением).

Величина поступления и дебиторской задолженности устанавливается исходя из цены, зафиксированной в договоре между поставщиком и покупателем (заказчиком) или пользователем активов предприятия. Если цена не определена в договоре и не может быть установлена исходя из его условий, то для установления величины поступления и дебиторской задолженности принимается цена, по которой в сравнимых условиях предприятие определяет выручку в отношении аналогичной продукции, либо предоставления во временное пользование аналогичных активов.

При продаже продукции и товаров на условиях коммерческого кредита, предоставляемого в форме отсрочки и рассрочки оплаты, выручка принимается к учету в полном объеме дебиторской задолженности.

Суммы поступления и дебиторской задолженности по договорам, предусматривающим исполнение обязательств (оплату) неденежными средствами, принимаются к бухгалтерскому учету по стоимости товаров, полученных предприятием. Стоимость товаров, полученных или подлежащих получению предприятием, определяется исходя из цены, по которой в сравнимых условиях оно устанавливает стоимость аналогичных товаров. При изменении обязательства по договору первоначальная величина поступления и дебиторской задолженности корректируется исходя из стоимости активов, подлежащих получению предприятием. Стоимость активов, подлежащих получению предприятием, устанавливается исходя из цены, по которой в аналогичных обстоятельствах предприятие исчисляет стоимость таких же активов.

Величина поступления и дебиторской задолженности устанавливается с учетом всех предоставленных предприятию договорных скидок (накидок). При формировании в соответствии с правилами бухгалтерского учета резервов сомнительных долгов величина выручки от реализации не изменяется.

В состав операционных доходов включаются:

• 1)    поступления, связанные с предоставлением за плату во временное пользование активов предприятия;

• 2)    поступления, связанные с предоставлением за плату прав, возникающих из патентов на изобретения, промышленные образцы и другие виды интеллектуальной собственности;

• 3)    поступления от участия в уставных капиталах других организаций (включая проценты и дивиденды по ценным бумагам);

• 4)    прибыль, полученная предприятием в результате совместной деятельности (по договору простого товарищества);

• 5)    поступления от реализации основных средств и иных активов, отличных от денежных средств (кроме иностранной валюты), продукции и товаров;

• 6)    проценты, полученные за предоставление в пользование денежных средств организации, а также проценты за использование банком денежных средств, находящихся на ее счете в этом банке.

Внереализационными доходами являются:

• 1)    штрафы, пени, неустойки за нарушение условий договоров;

• 2)    активы, полученные безвозмездно, в том числе по договору дарения;

• 3)    поступления в возмещение причиненных предприятию убытков;

• 4)    суммы кредиторской и депонентской задолженности, по которым истек срок исковой давности;

• 5)    курсовые разницы по валютным операциям;

• 6)    сумма дооценки оборотных активов;

• 7)    прочие внереализационные доходы.

Чрезвычайными доходами считаются поступления, возникающие как последствия чрезвычайных обстоятельств хозяйственной деятельности (стихийного бедствия, пожара, аварии, национализации и т. д.)

Выручка от реализации признается в бухгалтерском учете при наличии следующих условий:

• 1)    предприятие имеет право на получение выручки, обусловленное конкретным договором;

• 2)    сумма выручки от реализации может быть достоверно подсчитана;

• 3)    существует уверенность в том, что в результате конкретной операции произойдет увеличение экономических выгод предприятия;

• 4)    право собственности (владения, пользования и распоряжения) на продукцию (товар) перешло от предприятия-поставщика к покупателю или работа принята заказчиком;

• 5)    расходы, которые произведены в связи с коммерческой операцией, могут быть определены.

Если в отношении денежных средств и иных активов, полученных предприятием в оплату, не соблюдается хотя бы одно из названных условий, то в бухгалтерском учете предприятия отражается кредиторская задолженность, а не выручка от реализации. Предприятие вправе признать в бухгалтерском учете выручку от реализации продукции с длительным циклом изготовления по мере готовности данной продукции (работы, услуги) или по завершению изготовления продукции в целом. Выручка от реализации конкретного изделия (работы, услуги) признается в бухгалтерском учете по мере готовности, если возможно установить готовность изделия, работы, услуги.

В отношении различных по характеру и условиям выполнения работ, оказания услуг, изготовления изделий предприятие может использовать в одном отчетном периоде одновременно разные способы признания выручки от реализации.

Если выручка от продажи продукции (работ, услуг) не может быть достоверно установлена, то она принимается к бухгалтерскому учету в размере признанных расходов по изготовлению данной продукции, которая будет оплачена предприятию в будущем.

Метод определения выручки от реализации устанавливается предприятием при принятии учетной политики на предстоящий год исходя из условий хозяйствования и заключенных договоров.

Выручка от реализации продукции (товаров) учитывается в кредите счета № 46; выручка от реализации основных средств и иного имущества – в кредите счета № 47; выручка от реализации прочих активов – в кредите счета № 48.

Выручка от продажи продукции (товаров) классифицируется на два типа:

• 1)    выручка (брутто) от реализации продукции (товаров, работ, услуг), включая косвенные налоги;

• 2)    выручка (нетто) от реализации продукции (товаров, работ, услуг) без косвенных налогов (НДС, акцизов, таможенных пошлин).

ЧВР = ВВР – Косвенные налоги,                                            (18)

где ЧВР – чистая выручка от реализации;

ВВР – валовая выручка от реализации.

Наряду с абсолютными значениями в процессе управления выручкой от реализации используются относительные показатели.

• 1.    Коэффициент доли чистой выручки от реализации ( К_чвр ):

• 2.    Уровень отдачи активов предприятия:

К чвр = ЧВР / ВВР .                                                                 (19)

Этот показатель дает представление об объеме налогообложения валовой выручки от реализации.

Уоа = ВВР(ЧВР) / А, где А - средняя стоимость используемых активов за расчетный период (квартал, год).

Этот показатель характеризует способность активов генерировать валовую (чистую) выручку от реализации. Объем выручки от реализации продукции зависит от таких факторов, как:

• 1)    уровень реализационных цен;

• 2)    объем реализации произведенной продукции;

• 3)    уровень налогообложения ВВР .

Приведенные факторы носят агрегированный характер, т. е. сами складываются под влиянием факторов второго порядка – емкости товарного рынка, уровня конкуренции, номенклатуры производимой продукции, форм расчетов за продукцию (денежные расчеты, бартерный обмен, взаимозачеты) и др.

Рассмотренные факторы позволяют обеспечивать механизм управления формированием ВВР и ЧВР . Основу этого механизма составляют:

• 1)    формирование рациональной ценовой политики;

• 2)    планирование (прогнозирование) выручки от реализации.

Оптимизация Po, Do, Z в усложненном варианте (для случая F_m ( V_i, K_j ) = Po = Do = = Z ^ max, при i = 4, j = 2)

Адаптация базы данных к новым условиям

Ранее² мы рассматривали задачи, в условии которых присутствовал единственный неизменный параметр – выручка V . Теперь, в режиме последовательного усложнения, будем решать задачу с несколькими неизменными параметрами. Цель : помочь предпринимателям самостоятельно строить математические модели, описывающие далеко не простые ситуации, и использовать их в своей практической работе.

Будем считать, что предприятие имеет основные фонды, в стоимостном выражении равные Ф , причем норма амортизации n для них директивно определена (например, для компьютеров, n = 0,125, т. е. нормативный срок их службы составляет 8 лет (1 /0,125=8).

Существующее законодательство в ряде случаев разрешает применять «ускоренную» норму амортизации, вводя к действующей норме повышающий коэффициент (обозначим его K ₂), не превышающий 2. Причем значение этого коэффициента в пределах от 1 до 2 предприятие может устанавливать самостоятельно.

Целью нашего исследования будет определение оптимального значения коэффициента ускорения амортизации K ₂.

В предшествующих главах было показано, что целесообразно всемерно снижать размер затрат S_m + S_o , сводя их к минимально возможной величине. Опираясь на этот вывод, будем считать, что эта минимальная величина и зафиксирована как определенная доля S_o в выручке V .

Таким образом, мы должны внести в постановку задачи и формулы (5–12) следующие изменения:

• 1)    заданы 4 неизменных параметра:

• V ₁ = V – планируемая выручка;

• V ₂ = Ф – стоимость основных фондов;

• V ₃ = n – стандартная норма амортизации;

• V ₄ = S_o – доля материальных и прочих затрат в выручке V ( S_o < 1);

• 2)    в качестве управляющих снова выберем 2 параметра K ₁ и K ₂:

• K ₁ – удельный вес заработной платы Z в выручке V ;

• K ₂ – коэффициент ускорения амортизации;

• 3)    составим новые выражения (20–29) для функций F_m ( V_i , K_j ), которые для удобства сведем в таблицу 2;

• 4)    целевые функции по-прежнему будем выбирать из набора P_o , D_o , Z ;

• 5)    ограничения задачи:

безубыточность: P n > 0 рентабельность: R < 0,5 0 < K 1 < 1 1 2< 2.

Эта задача отличается от рассмотренных ранее тем, что теперь неизменный пара- метр V не является общим множителем для всех целевых функций и его величину надо задавать явно.

Кроме того, значения неизменных параметров не могут задаваться произвольно. Например, выручка V должна быть заведомо больше, чем стоимость амортизации основных фондов n Ф при директивно заданной норме амортизации. Иначе требование безубыточности (30) будет нарушено при любых S_o , K₁ и K₂ , т. е. область допустимых значений управляющих параметров будет пуста .

Для учета таких взаимосвязей между параметрами экономической ситуации, в которой находится предприятие, и требуется создание математических моделей, подобных рассматриваемой.

С учетом сделанной оговорки примем следующие значения неизменных параметров нашей модели в некоторых условных единицах измерения:

• V = 1000, S_o = 0,1,      Ф = 100, n = 0,125.

Подставляя выбранные значения неизменных параметров в формулы (20–29) (табл. 2), получаем:

• Z = 1 000 K₁ ;

  
  

P_o = 654 – 1 060 K₁ – 9,5 K₂ ;

D_o = 654 – 60 K₁ + 3,0 K₂ , аналогично с ограничениями: 0 < K₁< 1

• 1    2< 2.

безубыточность : 1 395 K₁ + 12,5 K₂ 860 рентабельность : 2 077,5 K₁ + 18,75 K₂ 812,5.

Как видим, несмотря на существенное (в четыре раза) возрастание числа неизменных параметров и кажущейся сложности задачи, конечные модели (31 и 32) получились простыми как для целевых функций, так и ограничений и могут быть проанализированы рассмотренным выше графическим методом, т. к. после упрощений линейные выражения содержат только два параметра K₁ и K₂ .

Для лучшего визуального восприятия, выполним графическую интерпретацию задач оптимизации P_o , D_o , Z на совмещенных рисунках 4а и 4б. Из системы ограничений (32) определим множество допустимых значений М и его границы: А (0,6; 2), B (0,61; 1), С (0,382; 1), E (0,373;2).

Таблица 2

Старые выражения (модели)		Новые выражения (модели)
Формула	Код	Формула	Код
Заработная плата в составе себестоимости
Z = К, х V		Z = К, х V	(20)
Налоги
Nzs = 0,385 х К, х V Nvs = 0,025 х V		Nzs = 0,385 х К, х V Nvs = 0,025 х V	(21) (22)
Себестоимость продукции S и прибыль Р
S = Z + N7. + N + S + S + Sn = = (0,025 + 1,385хК, + K2) x V, где К2- уд. вес. (Sm+ So) в выручке V, a Sa = 0 Р = V - S = (0,975 - 1,385 х К, - К2) х V	(4) (5)	S=(So+0,025+1,385 х К,) х V + п х К2 х Ф где So - доля материальных и прочих затрат в выручке V, причем So<1; К2- коэффициент ускорения амортизации. Р = V - S = (0,975 - S - 1,385 х х К,) х V-n х К2 х Ф	(23) (24)
Прочие налоги, относимые на хозяйственные результаты (без изменений)
Nh= 0,015 х V + 0,01 х Z = (0,015 + + 0,01 х К,) х V		Nh = (0,015 + 0,01 xK,)xV.	(25)
Налогооблагаемая (PJ и остаточная (PJ прибыль
Pn = Р - Nh = (0,960 - 1,395 х К, - К,) х х V>0 Ро = 0,7 х Рп= (0,672 - 0,9765 х К, - 0,7 х К2) х V		Pn= Р - Nh= (0,96 - So- 1,395 x x К,) x V - n x K2 x Ф Ро= 0,76 х Pn= (0,73-0,76 х xSo-1,060xK1)xV- 0,76 х п х К2 х Ф - для рис. 4а Ро= 0,7 х Рп= (0,672 - 0,7 х So -- 0,9765 х К,) х V - 0,7 х п х К, х х Ф - для рис. 46	(26) (27)
Остаточный доход D„
Do= Z + Ро= (0,672 + 0,0235 х К,-0,7 х х К2) х V	(8)	Do=Z + Po+Sa Do= (0,73 - 0,76 х So- 0,060 х х К,) х V + 0,24 х п х К2 х Ф -для рис. 4а; Ро = 0,76 х Рп D° = (0,672 - 6,7 х So+ 0,0235 х х К,) х V + 0,3 х п х К2 х Ф; для рис. 46; Ро = 0,7 х Рп	(28)
Рентабельность (< 0,5)
R = P/S = [(0,975 - 1,385 х К, -К2)/(0,025 + 1,385 х К, + К2)] < 0,5, т. е. 2,0775 х К, + 1,5 х К2 > 0,9625		R = P/S = [(0,975 - So- 1,385 х х К,) х V-n х К2 х Ф)/(0,025 + + So+ 1,385 х К,) х V + п х К2 х Ф)] < 0,5 т. к° V = 1 000, So= 0,1, Ф = 100, п = 0,125 [(0,975 -0,1 -1,385 х К,) х 1000-0,125 х100хК2)/(0,025 + + 0,1 + 1,385 х К,) х 1000 + + 0,125 х 100 хК2)]< 0,5 (875 - 1385 х К,-12,5 х х К2)/(125 + 1385 х К, + 12,5 х К2) < 0,5 2077,5 х К, + 18,75 х К, > 812,5	(29)

Примечание . В расчетах учтено изменение налога на прибыль, если раньше P_o = 0,7х P_n , то теперь P_o = 0,76 х P_n , причем в новых моделях для сравнения рассматриваются оба варианта.

A =

B

C =

E

K₂ = 2

1395 K 1 + 12,5 K₂ = 860 ^ K 1 = (860 - 12,5 x 2) / 1395 « 0,598 ^ A(0,6; 2).

K₂ = 1

1395 K 1 + 12,5 K₂ = 860 ^ K 1 = (860 - 12,5) / 1395 » 0,607 ^ B(0,61; 1).

K₂ = 1

2077,5 K 1 + 18,75 K₂ = 812,5 ^ K 1 = (812,5 - 18,75) / 2077,5 » 0,382 ^ C(0,382; 1).

K₂ = 2

2077,5 K 1 + 18,75 K₂ = 812,5 K 1 = (812,5 - 18,75 2)/2077,5 » 0,373 ^ E(0,373; 2).

Очевидно, что множество всех точек x е M содержится в четырехугольнике dABCE. С помощью градиентов V P o , V D o , VZ теперь без труда можно найти оптимальные точки. Рисунки 4а и 4б требуют небольшого пояснения, т. к. их оформление не совсем согласуется с изложенным способом решения задач: точка x выбрана за внешними границами M с привязкой к ней градиентов V P o , V D o , V Z и линий уровня целевых функций P o , D o , Z только для того, чтобы освободить множество М от большого количества линий и векторов.

Максимум остаточной прибыли

Математическая модель задачи:

F m ( V, K j ) = P o = 654 - 1 060 K 1 - 9,5 K₂ ^ max 0 < K i <  ¹ 1 2< 2

безубыточность : 1 395 K 1 + 12,5 K₂ 860 рентабельность : 2 077,5 K 1 + 18,75 K₂ 812,5.

На рисунке 4а видно, что точка E (0,373; 2) является оптимальной, следовательно:

P o ( E) = 654 - 1 060 x 0,373 - 9,5 x 2 = 239,62.

Максимум остаточного дохода

Математическая модель задачи отличается от (33) лишь записью целевой функции Do: F_m ( V, K) = D o = 654 - 60 K 1 + 3 K₂ ^ max .

Точка E (0,373; 2) вновь является оптимальной (рис. 4а):

D o ( E ) = 654 - 60 x 0,373 + 3 x 2 « 637,62.

Максимум заработной платы

По аналогии с предыдущими моделями:

F m ( V, K j) = Z = 1 000 K 1 ^ max.

Из самой аналитической формы функции Z видно, что ее максимум достигается при максимально возможном K₁ . Однако совокупность ограничений (32) вносит свои коррективы, и на рисунках 4а и 4б мы видим, что оптимальной является точка B (0,61; 1).

Z = 1 000 x 0,61 = 610.

Обобщенные выводы по критериям Po, Do, Z

Полученные новые результаты можно представить в виде таблицы 3 (вариант P_o = 0,76 P_n ) и таблицы 4 (вариант P_o = 0,7 P_n ), которые ЛПР и должен использовать, принимая решение о целесообразности введения ускоренной нормы амортизации основных фондов.

Критерий оптимизации	Соответствующие значения экономических показателей
	Po	Do	Z	sa
Po	239,65	637,62	373	25
Do	239,65	637,62	373	25
Z	-2,1	620,4	610	12,5

Таблица 3

Из таблицы видно, что при оптимизации заработной платы Z (и заданных значениях неизменных параметров: V = 1 000, So = 0,1, Ф = 100, n = 0,125) нецелесообразно вводить ускоренную амортизацию.

Справочно: P o = (0,73 - 0,76 x S o - 1,060 x K 1 ) xV - 0,76 xn x K 2 x Ф ;

D o = (0,73 - 0,76 xS o - 0,060 xK 1 ) x V + 0,24 x n x K 2 хФ ;

Z = K 1 x V ; S a = n x K 2 xФ .

Критерий оптимизации	Соответствующие значения экономических показателей
	Po	Do	Z	sa
Po	220,266	618,266	373	25
Do	-1,4	623,6	600	25
Z	-2,476	620,085	610	12,5

Таблица 4

Из таблицы видно, что при заданных значениях 4-х неизменных параметров: V = 1 000; So = 0,1; Ф = 100; n = 0,125 нецелесообразно вводить ускоренную амортизацию при оптимизации не только заработной платы (Z), но и остаточного дохода предприятия (Do).

Справочно:

P o = 0,7 P n = (0,672 - 0,7 S o - 0,9765 K 1 ) xV - 0,7 xn x K 2 xФ = 602 - 976 K 1 - 8,75 K 2 ;

D o = Z + P o + S a = (0,672 - 0,7 S o + 0,0235 K 1 ) xV + 0,3 xn x K 2 x Ф = 602 + 23,5 K 1 + 3,75 K 2 ;

Z = 1 000 K 1 ;

S_a = 12,5 K₂ .

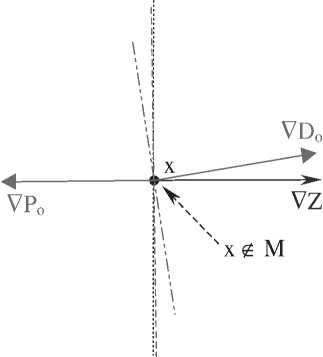
На рисунке 4б видно, что оптимальная точка для P_o – E (0,373; 2); оптимальная точка для D_o – A (0,6; 2); оптимальная точка для Z – B (0,61; 1).

Вычислим значения экономических показателей в оптимальных точках:

Е (0,373; 2)        P o = 602 - 976,5 x 0,373 - 8,75 x 2 « 220,266;

Z = 1 000 x 0,373 = 373;

S a = 12,5 x2 = 25;

Z = 1 000 x 0,6 = 600;

S a = 12,5 x2 = 25;

S a = 12,5 x 1 = 12,5.

D o = 602 + 23,5 x 0,373 + 3,75 x 2 «618,266;

A (0,6; 2)          D o = 602 + 23,5 x 0,6 + 3,75 x 2 « 623,6;

P o = 602 - 976,5 x 0,6 - 8,75 x 2 «-1,4;

B (0,61; 1)

Z = 1 000 x 0,61 = 610;

P o = 602 - 976,5 x 0,61 - 8,75 x 1 « -2,476;

D o = 602 + 23,5 x 0,61 + 3,75 x 1 « 620,085;

K2>	к              Po	'd0
2,0	E(0,373; 2)
	E(0,373; 2) i i i i i	M
	R	i
1,0	C(0,382; 1)	i i i
	Do;	po

z

A(0,6; 2)

B(0,61; 1)

Z

0,38       0,61                 1,0

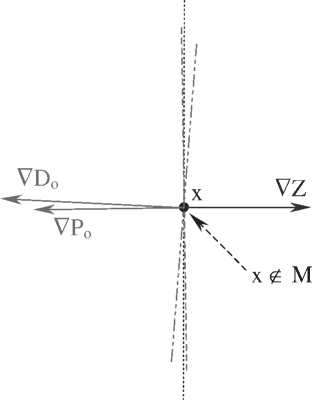
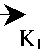
Рис. 4а. Графическая интерпретация задач оптимизации P_o , D_o , Z на совмещенном рисунке (для случая i = 4, j = 2, P_o = 0,76 х P_n )

P o = 0,76 P n = (0,73 - 0,76 S_o - 1,06 K 1 ) x V - 0,76 x n x K 2 x Ф = 654 - 1 060 K 1 - 9,5 K ₂;

D o = Z + P o + S a = (0,73 - 0,76 xS o - 0,06 x K 1 ) x V + 0,24 x n x K 2 xФ = 654 - 60 K 1 + 3 K 2 ;

Z = 1000 K 1 .

Z

О

0,38       0,61

1,0

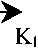
Рис. 4б. Графическая интерпретация задач оптимизации P_o , D_o , Z на совмещенном рисунке (для случая i = 4, j = 2, P_o = 0,70 х P_n )

P o = 0,7 P n = (0,672 - 0,7 S o - 0,9765 K 1 ) x V - 0,7 x n x K 2 x Ф = 602 - 976,5 K 1 - 8,75 K ₂;

D o = Z + P o + S a = (0,672 - 0,7 S o - 0,0235 K 1 ) x V + 0,3 x n x K 2 хФ = 602 - 23,5 K 1 + 3,75 K 2 ;

Z = 1000 K 1 .

Максиминная задача оптимизации денежных доходов работников (алгоритм Гросса)

Основная идея.

Составить первичное назначение. Составить соответствующую матрицу, решить для нее задачу о наибольшем паросочетании и если по-прежнему удается найти полное паро-сочетание, снова попробовать видоизменить матрицу, запомнив значение функционала. Этот алгоритм указал Гросс.

Возможные сложности.

• 1.    Как составить первое паросочетание?

• 2.    Как видоизменять матрицу, чтобы следующий результат (значение функционала) был не хуже предыдущего?

• 3.    Когда завершать процесс улучшения значения функционала?

Способы преодоления.

• 1.    Для начального назначения выбрать диагональные элементы матрицы, т. е.

• 2.    Порождение матрицы В производится по правилу: b[i, j] = 1, если размер зарплаты при назначении i-го работника на j-ю должность меньше найденного на предыдущем шаге значения функционала и b[i, j] = 0 в противном случае.

• 3.    Признаком окончания итерационного процесса является невозможность на определенном этапе построить наибольшее паросочетание. Тогда лучший результат и соответствующее назначение найдены на предыдущем шаге.

1-го работника назначить на 1-ю должность, 2-го – на вторую и т. д.

Формальное описание алгоритма Гросса.

Ввод :

A[i, j];

Инициализация :

p[M] – начальное назначение, присвоить p = (1, 2,...,M) (число на i-м месте показывает номер работы, на которую назначен i-й человек);

f – значение функционала, присвоить f = Max(a[i, i]) (максимальный элемент на главной диагонали);

Общий шаг :

• 1.    Породить матрицу В

• 2.    Использовать Алгоритм нахождения наибольшего паросочетания, ввод – матрица В, вывод – матрица Nas_u.

• 3.    Проверить, является ли паросочетание наибольшим:

в цикле по i от 1 до M в цикле по j от 1 до N если a[i, j]< f то b[i, j]=1 иначе b[i, j]=0

f_new: = Б (большое число).

В цикле по i от 1 до M если nas_u [i] ≠ -1, то:

если a[i, nas_u [i] < f_new, то f_new: = a[i, nas_u [i]]

иначе выход (паросочетание неполное и лучший результат был получен ранее).

f: = f_new (паросочетание наибольшее, обновляем значение функционала и лучшее назначение)

в цикле по i от 1 до M p[i]= nas_u [i]

Вывод :

P; f.

Задача

Назначить пять имеющихся сотрудников на вакантные должности так, чтобы самый большой размер оплаты труда оказался минимально возможным. Размер оклада (тыс. р. в месяц) приведен в таблице «Ввод: А(i, j) ».

Решение:

Категория постановки задачи – максиминная.

Способ решения – алгоритм Гросса.

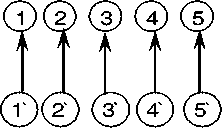
Общий шаг

1-я итерация, b(i, j)

	Г	2'	3'	4'	5'
1	0	1	1	1	1
2	1	1	1	1	1
3	0	1	1	1	1
4	1	1	1	1	1
5	0	1	1	0	1

2-я итерация, b(i, j)

	Г	2'	3'	4'	5'
1	0	0	1	1	1
2	1	1	1	1	1
3	0	1	0	1	1
4	1	1	1	1	1
5	0	1	0	0	1

3-я итерация, b(i, j)

	Г	2'	3'	4'	5'
1	0	0	0	1	0
2	0	0	0	1	1
3	0	1	0	0	0
4	0	0	0	0	0
5	0	1	0	0	0

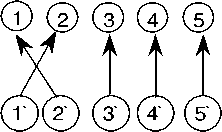
f_new - Б1 > < Б, при i = 1 находится новый функционал: а(1, 2) = 7 < 8 p(i) = Nas_u(i) = {2, 1,3. 4,5} f=7

Переходим к итерации 2

Для наглядности ребра u(i) = -1 на рисунке не показаны.

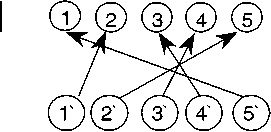
f_new = B2) < Бп, при i = 3 f_new: а[3, 4] = 4. Итак, f=4

p(i)=Nas_u(i)={5, 1,4, 3, 2} Переходим к 3-й итерации Для наглядности ребра u(i) = -1 на рисунке нс показаны.

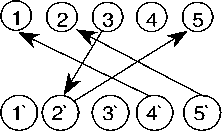
Построить наибольшее паросочетание не удается, т. к. вершина 4 заведомо ненасыщенная и[4] = О p(i)={4, 5,-1,0, 2}

Вывод: лучший результат и соответствующее назначение нацдены на предыдущем шаге (итерация 2).

Ввод: A(i,j)

i \	Г	2'	3'	4'	5"
1	8	7	5	3	4
2	5	4	4	2	3
3	8	2	7	4	4
4	5	6	5	4	4
5	8	3	7	9	4

Инициализация:

f=Б (большое число)

В цикле по 1 от 1 до 5, по j от 1до 5 p(i) = i, т. е. Nas_u = [1, 2, 3, 4, 5] f = 8, т. к f=max (a[i, i]) (макс, элемент из главной диагонали)

Ответ. P = {5, 1, 4, 3, 2} F = 7.

Вывод. Решая и реализуя максиминную задачу на практике, работодатель предупреждает социальную напряженность в трудовом коллективе, т. к. не допускает аморального разрыва между доходами низко и высокооплачиваемых работников, который в рекомендуемом варианте составляет 66,6…% (5/3100 – 100), а в развратном – 300% (8/2100 – 100).

Замечание . Такие задачи рекомендуется решать, а результаты внедрять при создании новых предприятий, т. е. на старте. Далее, когда предприятие встало на ноги и уверено в удержании своего устойчивого финансового положения, можно и даже нужно переходить к решению задачи оптимального назначения сотрудников на вакантные должности так, чтобы суммарный фонд заработной платы был максимальным. А это уже максисуммная постановка задачи, которая решается по алгоритму Егервари (алгоритм, написанный венгром Егервари еще в 1931 году).

Заключение

Сегодня во всем мире признается приоритет экономики в обеспечении внутренней и внешней безопасности государств, в регулировании социальных отношений, складывающихся в отношении производства и распределения благ в обществе на базе основополагающих принципов: эффективности производства, выражающегося в снабжении граждан государства максимальным количеством продуктов при заданном объеме затрат или в выпуске заданного количества продуктов при минимальном объеме затрат; справедливости распределения благ, выражающегося в стремлении сгладить неравенство доходов граждан страны и в увеличении доходов каждого по его вкладу в рост эффективности производства; стабильности экономической жизни государства при низких темпах инфляции и безработицы.

Конечный продукт для граждан государства или конечный продукт производственного назначения складывается из следующих продуктов:

• •    для потребительского рынка;

• •    для развития инфраструктуры - науки, культуры, здравоохранения, жилищно-коммунального хозяйства, бытового обслуживания, пассажирского транспорта и связи;

• •    оборонного назначения;

• •    для резервов на случай чрезвычайных ситуаций;

• •    для внешнеэкономической деятельности.

Исходя из государственных приоритетов должно определяться оптимальное распределение национальных ресурсов по каждому непроизводственному направлению конечного продукта.

В соответствии с принципом эффективности производства желательно использовать национальные ресурсы таким образом, чтобы получить быстрый рост конечного продукта непроизводственного назначения в оптимальном ассортименте при обоснованном распределении доходов и стабильности государства. Координация роста доходов граждан в зависимости от их вклада в рост эффективности производства и сглаживание неравенства их доходов становятся основой внутренней экономической безопасности. Для гарантии стабильности государства нужен не только быстрый рост, но и устойчивое увеличение темпов экономического роста на базе развития отраслей как определяющих научно-технический прогресс, так и обеспечивающих сбалансированное развитие экономики и достижение полной занятости исходя из динамики структуры конечного спроса. Естественно, что при этом обеспечивается и стабильность национальной валюты.

Для решения этих и других конкретных задач и применяются экономико-математические методы и модели, рассмотренные в настоящей статье.