Приложение двойных интегралов
Автор: Гильманова Г.Р.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 9 (15), 2016 года.
Бесплатный доступ
Статья посвящена приложению двойных интегралов. В статье рассматриваются их геометрические и физические приложения. Представлены формулы для решения двойных интегралов с разными способами, а также решены некоторые задачи.
Двойные интегралы, геометрические приложения, физические приложения, площадь, объем
Короткий адрес: https://sciup.org/140269760
IDR: 140269760
Текст научной статьи Приложение двойных интегралов
Геометрические приложения двойных интегралов
Площадь плоской фигуры
Если f (x,y) = 1 в интеграле
Jp(^^)^^ „ „
s , то двойной интеграл равен площади области интегрирования R.
Площадь области типа I (элементарной относительно оси Оy) (рисунок 1) выражается через повторный интеграл в виде аг№
Аналогично, площадь области типа II (элементарной относительно оси Оx) (рисунок 2) описывается формулой
Л = J J dxdy.
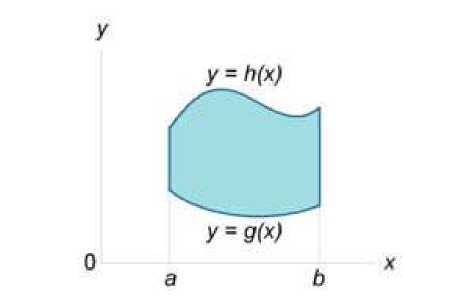
Рис.1
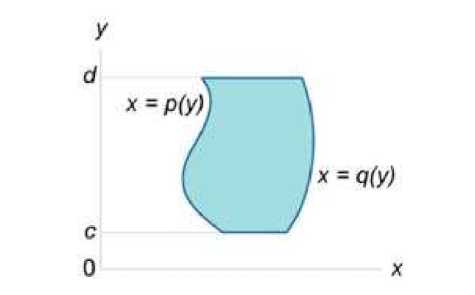
Рис.2
Объем тела
Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой
М1л^уИ-
В случае, когда R является областью типа I, ограниченной линиями
I x = й, x = b, y=h(y, ^ = g(x)
, объем тела равен
»st”) ^JJVl^)13^ J J /^,y)dydx.
Для области R типа II, ограниченной графиками функций y=c, y = d, x = q$, x=p(y)
, объем соответственно равен d #0)
r = jj/(x,iy)tti = J J y.x,y")dxdy. S C X?)
Если в области R выполняется неравенство , то объем цилиндрического тела между поверхностями z1 = f (x,y) и z2 = g (x,y) с основанием R равен
^■fJ^fM-st1^)]^
Площадь поверхности
Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой
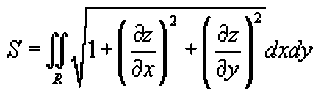
при условии, что частные производные 3x и области R.
Ф7
непрерывны всюду в
Площадь и объем в полярных координатах
Пусть S является областью, ограниченной линиями
8 = a, 8 = p, r=h^Y r=g(8)
(рисунок 3). Тогда площадь этой области определяется формулой
^s(.e)
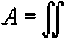
dM = J J rdrd8.
s « 6(e)
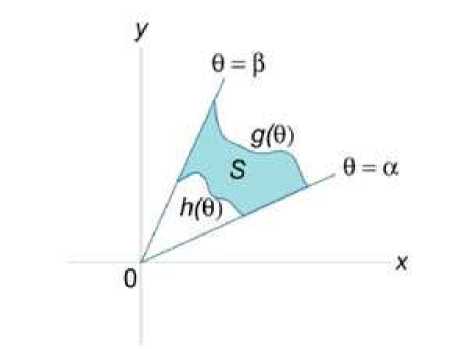
Рис. 3
2 = fV^
Объем тела, ограниченного сверху поверхностью с основанием S, выражается в полярных координатах в виде F = JJf(x,8)xdrd8.
Пример
2 2
у = a - ах, у = a + x
Вычислить площадь области R, ограниченной линиями
Решение.
Сначала определим точки пересечения двух заданных линий.
у2 = а2 - ах у = а + х
^а + = д - ах, а2 + 2ах + х2 = а2 -ах, х2 + Зах = О,
^(л: + 3а) = О,
^2 = О, - За.
Следовательно, координаты точек пересечения равны
I Xj = О, ^ = а + О = а, л2 = -За, у2 = а - За = -2а.
Область R представлена на рисунке 5 выше. Будем рассматривать ее как область типа II. Для вычисления площади преобразуем уравнения границ:
у2 = а2 - ах => ах=а2-у2 или х = а-—, а у = а + х => х = у - а.
Получаем
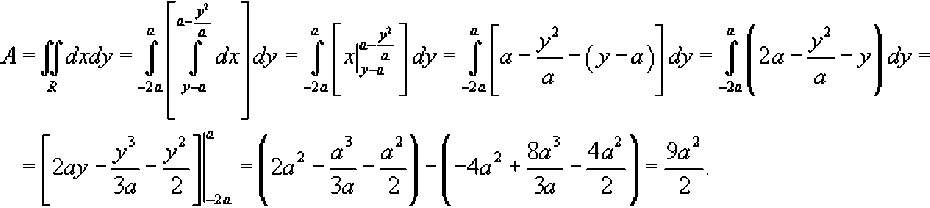
Физические приложения двойных интегралов
Масса и статические моменты пластины Предположим, что плоская пластина изготовлена из неоднородного материала и занимает область R в плоскости Oxy. Пусть плотность пластины в точке (x, y) в области R равна . Тогда масса пластины выражается через двойной интеграл в виде
™ = Л/?(х,^)йМ.
Статический момент пластины относительно оси Ox определяется формулой
M^ = jp^(x,.y)aL4
Аналогично находится статический момент пластины относительно оси Oy
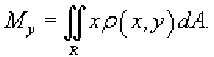
Координаты центра масс пластины, занимающей область R в плоскости /2 (л, у)
Oxy с плотностью, распределенной по закону , описываются формулами
м 1 „ fJM^)"
1 - — - “Я ^P^.yW - Tf-T--г--.
м 1 „ /М^.^)^
^ = —- = — (Гу^Х,^)^ = -4г;--------
Для однородной пластины с плотностью для всех (x, y) в области R центр масс определяется только формой области и называется центроидом.
Моменты инерции пластины
Момент инерции пластины относительно оси Ox выражается формулой
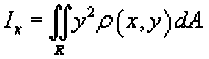
Аналогично вычисляется момент инерции пластины относительно оси Oy :
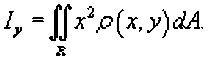
Полярный момент инерции пластины равен
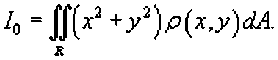
Заряд пластины
Предположим, что электрический заряд распределен по области R в плоскости Oxy и его плотность распределения задана функцией
Тогда полный заряд пластины Q определяется выражением
C’fpfM^
Среднее значение функции
Приведем также формулу для расчета среднего значения некоторой распределенной величины. Пусть f (x,y) является непрерывной функцией в замкнутой области R в плоскости Oxy. Среднее значение функции μ функции f (x,y) в области R определяется формулой
^■^If/tv)^- где S - площадь области интегрирования R.
Пример
Вычислить моменты инерции треугольника, ограниченного прямыми х+у =1, х = 0, .у = 0 Р^,У) = ?У
(рисунок 2) и имеющего плотность .
Решение.
Найдем момент инерции пластины относительно оси Ox.
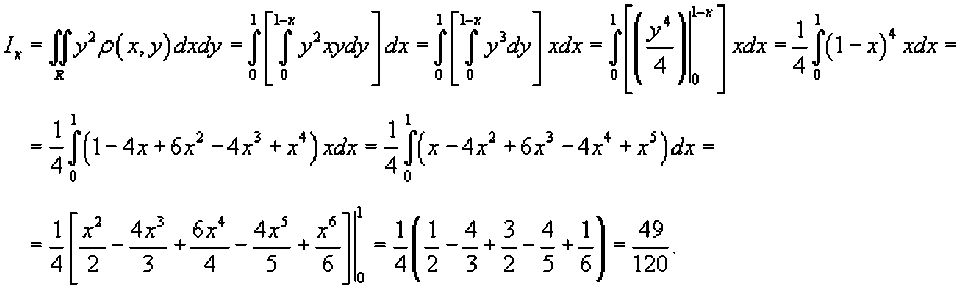
Аналогично вычислим момент инерции относительно оси Oy.
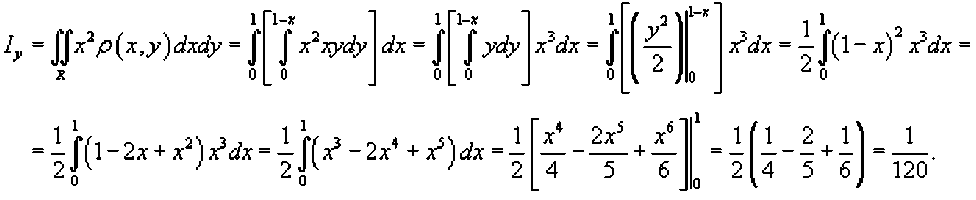
Список литературы Приложение двойных интегралов
- Фихтенгольц Г.М. «Курс дифференциального и интегрального исчисления» (II том) - Москва, 2013.
- Пискунов Н.С. «Дифференциальное и интегральное исчисления» (I том) - Москва, 2015.
- Эрмит Ш. «Курс анализа» - Москва, 2014


