Приложение криволинейных интегралов
Автор: Гильманова Г.Р.
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 1 (1), 2016 года.
Бесплатный доступ
Статья посвящена приложению криволинейных интегралов. В статье рассматриваются их геометрические и физические приложения. Представлены формулы для решения криволинейных интегралов с разными способами, а также решены некоторые задачи.
Криволинейные интегралы, геометрические приложения, физические приложения, закон ампера, закон фарадея
Короткий адрес: https://sciup.org/140276414
IDR: 140276414
Текст научной статьи Приложение криволинейных интегралов
Геометрические приложения криволинейных интегралов Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, с их помощью вычисляются
-
• Длина кривой;
-
• Площадь области, ограниченной замкнутой кривой;
-
• Объем тела, образованного вращением замкнутой кривой
относительно некоторой оси.
Длина кривой
Пусть C является гладкой, кусочно-непрерывной кривой, которая r (z),
cx
описывается вектором . Длина данной кривой выражается следующим криволинейным интегралом
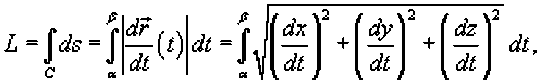
~ /at _____ „ -W. М z^ ____ _____„ где - производная, а - компоненты векторной функции
^)
Если кривая C задана в плоскости, то ее длина выражается формулой
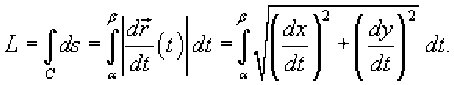
Если кривая C представляет собой график заданной явно, непрерывной v = /Uj и дифференцируемой функции в плоскости Oxy, то длина такой кривой вычисляется по формуле
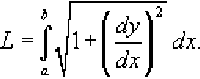
Наконец, если кривая C задана в полярных координатах уравнением
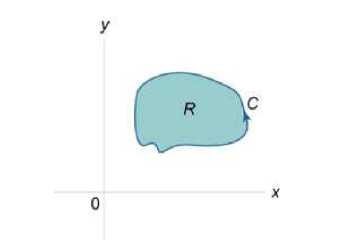
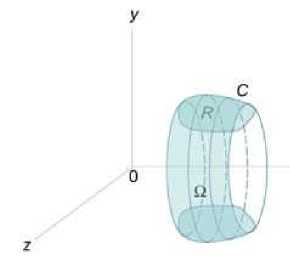
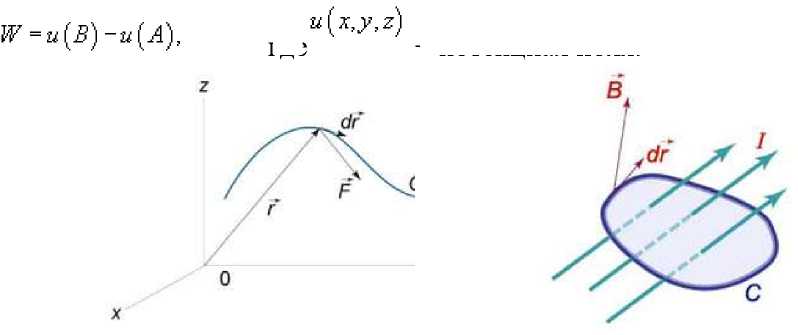
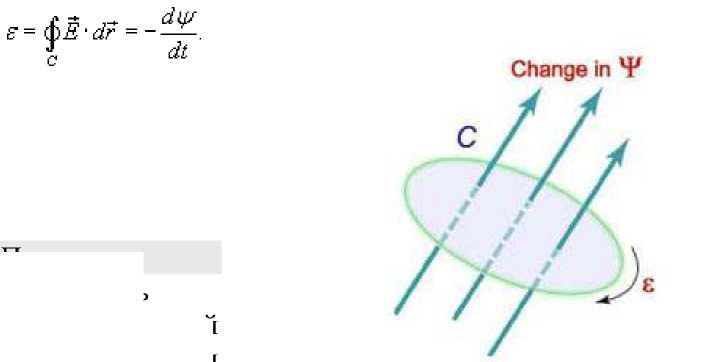
r=r(8), a<8 , и функция является непрерывной и [^, £] дифференцируемой в интервале , то длина кривой определяется выражением Площадь области, ограниченной замкнутой кривой Пусть C является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости Oxy (рисунок 1). Тогда площадь области R, ограниченной данной кривой, определяется формулами £ = ^xdy = -ф,уд?х = — sdy -ydx. c c ^ c Здесь предполагается, что обход кривой C производится против часовой стрелки. , то Если замкнутая кривая C задана в параметрическом виде площадь соответствующей области равна Рис.1 Рис.2 Объем тела, образованного вращением замкнутой кривой относительно оси Ox Предположим, что область R расположена в верхней полуплоскости y ≥ 0 и ограничена гладкой, кусочно-непрерывной и замкнутой кривой C, обход которой осуществляется против часовой стрелки. В результате вращения области R вокруг оси Ox образуется тело Ω (рисунок 2). Объем данного тела определяется формулами Физические приложения криволинейных интегралов С помощью криволинейных интегралов вычисляются Масса кривой; Центр масс и моменты инерции кривой; Работа при перемещении тела в силовом поле; Магнитное поле вокруг проводника с током (Закон Ампера); Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея). Рассмотрим эти приложения более подробно с примерами. Масса кривой Предположим, что кусок проволоки описывается некоторой пространственной кривой C. Пусть масса распределена вдоль этой кривой с плотностью ρ (x,y,z). Тогда общая масса кривой выражается через криволинейный интеграл первого рода Если кривая C задана в параметрическом виде с помощью векторной функции , то ее масса описывается формулой В случае плоской кривой, заданной в плоскости Oxy, масса определяется как или в параметрической форме Центр масс и моменты инерции кривой Пусть снова кусок проволоки описывается некоторой кривой C, а распределение массы вдоль кривой задано непрерывной функцией плотности ρ (x,y,z). Тогда координаты центра масс кривой определяются формулами где ^ = J^t^,^^)^, Мш = J^/?(x,y,z)^s, М^ = ^zp(x,y,z)ds с с с - так называемые моменты первого порядка. Моменты инерции относительно осей Ox, Oy и Oz определяются формулами ^ = /(У + z2)p(x,y,z)ds, с I, = +?'^p^,y,zx)ds, с 4 = J(^ + /)р(^,^)^-с Работа поля Работа при перемещении тела в силовом поле F вдоль кривой C выражается через криволинейный интеграл второго рода W = \F'dr, с где F - сила, действующая на тело, dr - единичный касательный вектор (рисунок 1). Обозначение F-dr означает скалярное произведение векторов Fи dr . Заметим, что силовое поле F не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы F иногда может оказаться отрицательной. Если векторное поля задано в координатной форме в виде F = ^P^,y,zyQ^,y,zYR^,y,z'1)y то работа поля вычисляется по формуле W = [F ■ dr = [Pdx + Qdy + Rdz. В частном случае, когда тело двигается вдоль плоской кривой C в плоскости Oxy, справедлива формула W = [F-dr =[Pdx + Qdy, c c F = [P(x,y),Q(x,yY Где Если траектория движения C определена через параметр t (t часто означает время), то формула для вычисления работы принимает вид где t изменяется в интервале от α до β. Если векторное поле F потенциально, то работа по перемещению тела из точки A в точку B выражается формулой где - потенциал поля. Рис.1 Рис.2 Закон Ампера Криволинейный интеграл от магнитного поля с индукцией В вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой д0 1.26x10 где - магнитная проницаемость ваккуума, равная Н/м. Закон Фарадея Электродвижущая сила ε, наведенная в замкнутом контуре C, равна скорости изменения магнитного потока ψ, проходящего через данный контур (рисунок 3). массу форму A(1,1) до от Рис.3 точки Масса Пример Определить проволоки, имеющей отрезка B(2,4). р^х,у) = Зх + 2у распределена вдоль отрезка с плотностью . Решение. Составим сначала параметрическое уравнение прямой _ УУл хУа УУл ' х-1у-1 => ----= -= 1, 2-1 4-1 х -1 у -1 => ----=----= t или \ = Z +1 AB. ^ = ^ + Г где параметр t изменяется в интервале [0,1]. Тогда масса проволоки равна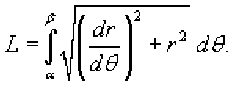
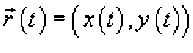
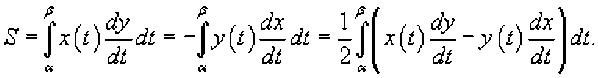

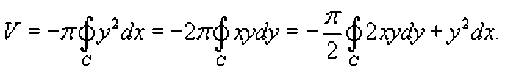
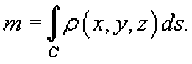
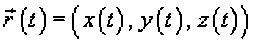
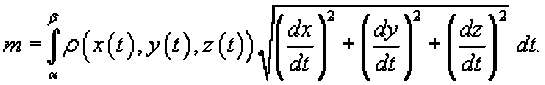
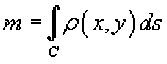
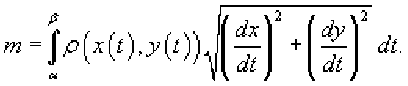
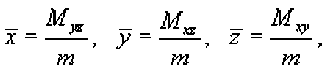
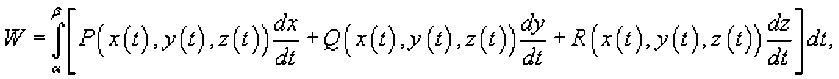
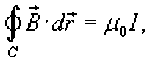
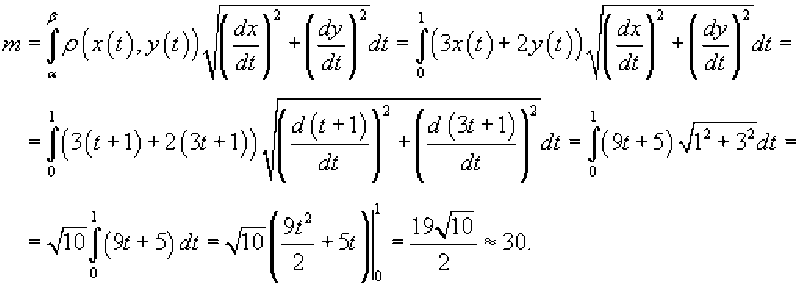
Список литературы Приложение криволинейных интегралов
- Фихтенгольц Г.М. «Курс дифференциального и интегрального исчисления» (II том) - Москва, 2013.
- Пискунов Н.С. «Дифференциальное и интегральное исчисления» (I том) - Москва, 2015.
- Эрмит Ш. «Курс анализа» - Москва, 2014


