Приложение моделей сверхзвуковых радиационных волн для описания пламени в поршневых двигателях

Обычно пламенные структуры описываются уравнениями типа Колмогорова – Петровского – Пискунова [1]:

D 1 — ₊ v ^ ₊ w_c 2(1 - c ) = o, c ( —^ ) = о, с ( _да ) = 1 . д z ²     д z

Автомодельная переменная z в (1) имеет вид волны z = (x - v t)/А шириной А, бегущей со скоростью v. Величина последней суть собственное значение краевой задачи. Искомая функция c(z) ассоциируется с формой перемещающих в пространстве концентраций, температурой, иными параметрами, D - с коэффициентом диффузии, W - с темпом превращения, сгорания, заражения или другой локальной трансформации среды. Формализм (1) применим для описания различных авто- и волновых процессов: фотодиссоциации газа под действием интенсивного УФ излучения [2], единичной волны на мелкой воде [3], адсорбции газа пористой средой [4]. Это позволяет использовать известные решения формально подобных задач для содержательно оригинальных постановок.

Покажем сводимость задачи [2] к уравнению (1). Модельная система уравнений переноса излучения и химической кинетики для фотодиссоциации газа имеет вид:

-- =   и cI ; — =  и cI ; I ( -» , t ) = I °; I ( ~ , t ) = 0; c ( -» , t ) = 0; c ( ~ , t ) = c ⁰,        (2)

дx         дt где x, t, I = I(x, t), c = c(x, t) - координата, время, интенсивность излучения и концентрация поглощающих частиц; с - сечение поглощения.

Ее решением служит

I ( x , t ) =

^{1 +} g

С 0

c ( x , t ) = — g -;

1 + g

g = exp

и c ⁰

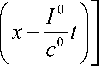
Решение (3) является автомодельным, что обусловлено законом сохранения частиц в элементарном фотохимическом акте. Автомодельной переменной служит z = и c ⁰ [ x - ( 1 ⁰ /с 0 ) t ] , что соответствует движению профилей I ( z ) и с ( z ) в невозмущенный газ со скоростью u F = I ⁰ /с 0 . Протяженность области фотореакции составляет l = 1/ и с 0 . В переменных I = I / 1 ⁰ , ё = с / с ⁰ с учетом консервативности I + ё = 1 уравнения (2) принимают вид:

т

|_ = -и с⁰1 (1 - 1 );     | c = -и 1⁰C (1 - C ) .                           (4)

д x                     д t

Работа выполнена при поддержке фонда ALCOA.

Дифференцируя уравнение (4) по автомодельной переменной, заменяя д I / д z в правой части результата на -о c ⁰ I (1 - I ) и умножая обе части результирующего уравнения на ( I^й/c °)(1/ о c °) , получаем:

1 ⁰ 1 9¹I I⁰ 91

-—■ + - + ² о I°1 ² х (1 - 1) = 0, I( -» ,t ) = 1, I ( да , t ) = 0 .               (5)

c o c d z   c d z

Идентичность уравнений (5) и (1) очевидна: роль коэффициента диффузии D играет комплекс ( I⁰/c °)(1/ о c °) , темпа локальной перестройки среды W - величина 2 о I ⁰. Собственное значение краевой задачи (2) v = 1⁰/c ⁰ совпадает с известной скоростью волны горения [1] v = ( WD /2) ^1/2 .

Аналогичные рассуждения позволяют установить связь уравнений (1) и (2) с солитонной моделью Кортевега – де Вриза (КдВ), описывающей эволюцию единичной волны на мелкой воде [4]. Введя новую функцию g ( z ) = dc ( z )/ dz , дифференцированием (1) и подстановкой в результат известного решения [1] с ( z ) = [1 + th( z / А )]/2 получаем уравнение КдВ:

g ' t ⁺ Agg ' х ⁺ Bg "' xxv = ⁰, g ( ^х - t ) = ⁰, g⁽ ^ ,t ) = ⁰ .                         ⁽⁶⁾

Здесь, если отвлечься от связи между скоростью, амплитудой и шириной импульса в солитоне КдВ, оказывается A = 3 ( WD /2) ^1/2 , B = (2 D ³/ W) ^1/2 и соответственно v = A /3, А = (12 B / А ) ^1/2 .

Практическая ценность проведенного в данной работе анализа состоит в выявлении реальной возможности распространить теоретические результаты работ [2, 5, 6] на описание ав-товолновых структур при горении в поршневых двигателях. В частности, предлагаются модели [2 5, 6] адаптирования для пламени с параллельно и последовательно протекающими реакциями в условиях обратимости тепловыделения при наличии источников вещества и энергии.