Приложение общей теории оболочек для учета краевого эффекта в тороидальном баке от внутреннего давления

Тороидальные баки высокого давления имеют широкое применение в аэрокосмической и военно-морской технике, а также в бытовой технике, например, в виде газобаллонного оборудования. Для расчета прочности баков от давления рассматривают безмоментное состояние с применением уравнения равновесия Лапласа [1–2].

В настоящее время компьютерное моделирование с помощью пакетов САПР позволяет решить самые сложные задачи проблемы прочности. Однако научный интерес, связанный с целью лучшего понимания механики деформирования конструкций, подталкивает исследователей заниматься математическим моделированием, полезным в том числе и для анализа решений, полученных с помощью прикладных программ.

Цель работы . Применив уравнения общей теории оболочек для расчета напряженно-деформированного состояния тора от внутреннего давления, проанализировать влияние изгибающих локальных моментных факторов так называемого краевого эффекта.

Постановка задачи. Используем уравнения общей теории оболочек В. З. Власова [3] в системе криволинейных координат OaeY. Здесь ось у — нормальная к базисной поверхности оболочки, находящейся в плоскости осей Оαβγ. Геометрические уравнения модели деформации представляются в форме рядов по переменной γ:

e aa =^£ a +K a Y + 9 a Y 2 ,

(1) ^евв =^s e ^{+ K} e Y + V e Y , e ae =^{m + T}Y + VY . ^v ’ которые были получены с помощью формул разложения коэффициентов первой квадратичной формы А = А (a, в), В = В (а, в) базисной поверхности:

■■ ИССЛЕДОВАНИЯ

Havko-

■ ГРАДА

¹      - ^{1            2}_v²_p_v3     ____¹____²_V²_^3_V³

A(1 + kЛ) = A(1  kЛ + kaY   kaY) 1  B(1 + kбТ) = B(1 kpY + kpY   kpY).

Символами k _α и k _β обозначены кривизны оболочки.

Компоненты разложения (1): e_a, е в , м, k _a, k в , т совпали с уравнениями, приведенными в [3]. Запишем компоненты φ_α, φ_β, ψ:

V a = k a k a w к

—

1 5 k --a v

B sp

—

1 d k

--- и +

A da

1 5 ² w   1 5 A dw)

—

A2 5a2 A3 5a 5a v

—

1 5 k _a 5 w    1 5 A 5 w ,

+              kB,

B2 5p 5p AB2 5p 5p p

V p = к p к p w к

—

1 d k p

v

—

1 d k p

B 5p A da

u +

1 5 ² w   1 5 B dw)

—

B2 dp2 B3 dp dp )

—

1 5 k , 5 w    1 5 B 5 w ,

—т   + —:--- k ,

A2 5a 5a A2B 5a 5a

V = ^k a ^k p

^л 1 5 u 1 5 v

—

—

+

к B dp A da AB dp

1 5A     1 5B ) ,

--u +---v + k,

^{+ k}в

( 1 5 u    1 5 A

—

к B dp AB dp )

^ u + k

' a

^{+ k} p

AB 5a ) ( 1 52 w

a

1 5 v

—

1 5B )

——v 1 +

A da AB da

2 5B dw )

f 1 5 ² w    2 5 A 5 w

к к

AB 5a 5p AB5a dp.

+

к AB 5a 5p A2B dp dav

1 5 k, 5 w   1 5 k 5 w

+--a— +--p —

AB 5p 5a AB 5a dp

.

На рис. 1 покажем принятые направления мембранных усилий и поперечных сил, а на рис. 2 - направления изгибающих и крутящих моментов.

В соответствии с принятыми на рис. 1 и 2 направлениями внутренних усилий и с учетом разложений (2) получены выражения:

3 N. =--- a   12(1 — ц 2 )

"h     / 1 5 A d w   1 5 A 5 w  1 5 k a     1 5 k a        1  5 B d w ) I k B k a )   1            1        +        v +        u ц -           + v p   a' k A 3 da 5a   A 3 da 5a   B 5p    A da      A 2 B da da J , 3      1 d k  d w  ,2,         1 d k p d w + k w             k k„w ц   7        + a     B 2 dp dp   a p      A 2 da da_

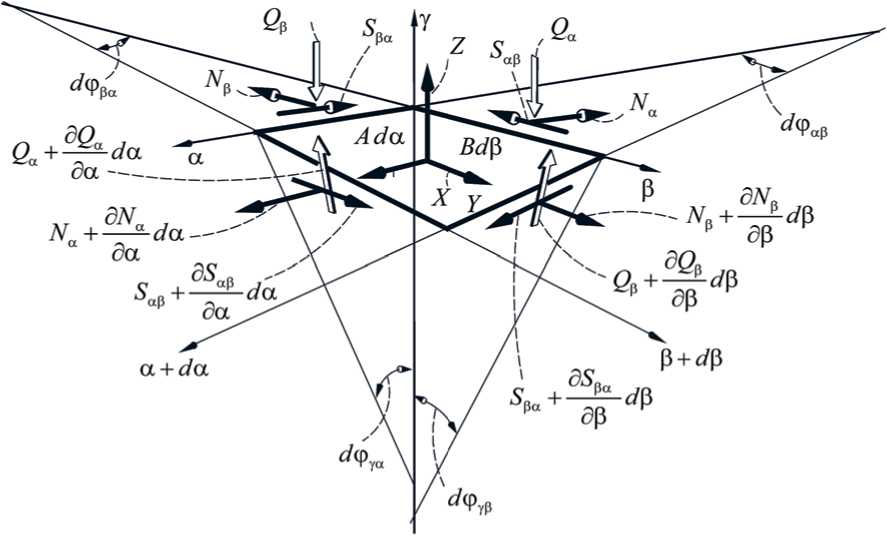
Рис. 1. Направления мембранных усилий и поперечных сил

+

Eh

(1—ц ² )

k a w ⁺ V

1 d u ,        1 d B

+ o k_Rw + ц       u +

A da ^p AB da

1 d A      1 d v ^л

--v + ц--

AB dp     B dp J

_V = Eh^{3 aP} 12(1 — ц²)

M = a

( ^k p ^{— k} a )

+2 k a k p

I 1 d² w    2 d B d w )

—

V

AB dadp AB ² da dp J

₂ .2 \ I 1 d v     1 d B ]

+1 k + k — v + ^{v a P}4 A da AB da J

1 d B    1 d v )   1 I d k _a d w 5 k в d w '

v +1

AB da A da) AB ( dp da da dp )

Eh

^{(1 —} Ц )

¹ d v

—— A da

1 d u    1 Id A    d B )

+— u + v

B dp AB (dp da J

+

Eh⁵    I ^k a ^k p d A dw

Ц

80(1 — Ц ² ) (    A³ da da

.       7 3 7           .       7     7

+ P k _a k ^ w +P k a ^k p

1 d ² w , ₂ 1 dB dw , A ² a?^{— e} B ³ ар ар^- *

±  d w +

B² dp dp

⁺ Ц ^k p

1    d A d w,k a k ^ d B d w   ,   1  d k p d w   ,2 1 d k e      ,2 1 д k _P| ,4   ₍

+            — k           — k       v — k       + k_R w +

AB² dp dp A ² B да da ^e A² da da ^e B dp ^e A da ^e

, 2 1 5² w     , ,

+ ^k в —2--2— M' ^k _a k e

B dp

1 д k

- v -Ц

B dp

k a k e ^d k a

A da

E h ³

+__

12(1 -Ц 2 )

( 1 д ² w 1 д Б dw , ,

--7— t +  --+ ^ kk w +

(   B ■ ^dP’-    B ^{3 d}P ^de ■

A u +

I

1    dB dw , ,

A ^ B a757^+M k -

^k p dv H dp

-H k a w +Ц

1 d k a b dp

v -

1 d A 1 d k „ 1 d k „          1 d u

--v + -v + -u + ц k„ AB dp B dp A da ^e A da

—

ц

1 д ² w

A ² да ²

+

1 d A d w ,   1 d B 1 d k _a 1 d A d w )

^{+ Ц} A³ да da ^{+ e} AB da u ^{+ Ц} A da u ^Ц AB² dp dp _v

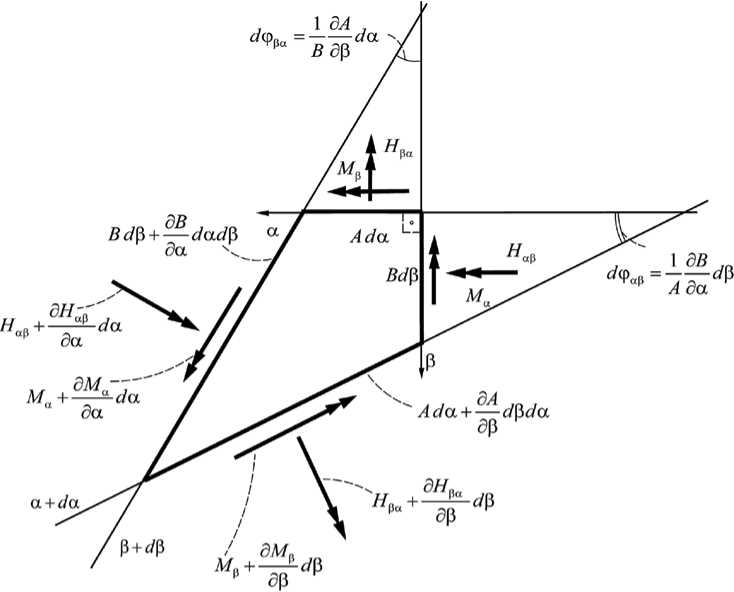
Рис. 2. Направления изгибающих и крутящих моментов

.      Eh³   ( к d v  k, d u   k _p d В   к d u     1   d В d w

= ^e 2 _^ v + -« + 2

“₽ 12(1 -p2) ( A da В dp A da В dp   AB2 da dp к da К db „ 1 d2 w „ 1 9a dw) au ■ v - 2+ 2—I.

AB dp AB da AB dadp AB dp da J

Усилия N e , M e , S e _a, H e _a симметричны усилиям (6)-(9) соответственно.

Воспользуемся уравнениями равновесия из [3], в которых учтем осевую симметрию:

d           dB

— (Na B) - N--+ QaAB ka + ABqa = 0, a       e      a      a       a

/Агм                    r /Агм

AB

7 B + Q     - (кaNa+ кв Nв ) + q Y= 0, da da J

Q a

1 dM„   1 d B_Z1,

- +      ( M a

А da АВ da

- M _R).

P'

Для этих уравнений изгибающие моменты и внутренние усилия приобретают вид:

Eh ⁵

Ma =------7“ a 80(1 — ц2)

Eh ³

+12(1 — Ц 2 )

, , 3      , , 1 д2 w , , 1 дВ 9 w цк6к^ + цк_к% -^ —7 + какв —;--- р a a р A2 da2 a р A2B da da

^{ц к} _р ^к _а w ^{— ц к} _а w

1 д ² w

А ² да ²

—

1 д В д w

А ² B да да

—

1 9 кв 9 w 4          1 9 ka k„—r —-— + кR w— ц к_к    - u р A2 da da р р A да

7 £ A да

u ^— Ц ^к р

1 д u 1 д² w

---ц—г--7

А да А ² да²

+

Eh ⁵

M r =------7"

^Р 80(1 — ц ² )

_к 1 д B д w “ А ² В да да

—

1 дкр д w                       1 д2 w кр —7—-— + ка кBw+ ц к,, w + ц к,, ——-р А да да р             А да

+

Eh ³

+--

12(1 — ц ² )

12(1 — ц ² )

, ,       1 дB д w ц д2 w , квк,^ -----у——к к р а А2B да да А2 да2   а

1 9 w

^{( к}а~ ^к р )^ ^Т ^{+ к}a w ^— А да

Eh                     Eh ³

+----- т" ( к_п +ц к о) w , Ж. =-------т" (1 — ц ² )^ ^а ^^{р7 р} 12(1 — ц ² )

ц д w

А да

— к 2 w

к р д к р д w _{к 2 к}     ( к _а — к р ) д В 9 w

А ² да да ^{а р} А² В да да

к a w —

J- ⁹Al ⁹ w А ² да да

^{— к}а^к р^{2 w}

Eh

+ — h— (ц к _а + к р ) w .

^{(1 —} ц)

В (10)–(12) Q _α – поперечная сила, а в (13)–(16) w = w (а) - функция прогиба. Обозначения: E - модуль Юнга; р. - коэффициент Пуассона; h - толщина стенки оболочки.

Введем тороидальную систему координат (рис. 3) и определим коэффициенты Ламе:

А = R , В = R +—.       (17)

sin “

Выражение (12) после подстановки в него (17) приобретает вид

1 dM _a        a cos a

^{Q a}=o"^7-- ^{( M} “^{— M} р ). ⁽¹⁸⁾

R d a    R sin a ( a + R sin a )

Обратим внимание на знаменатель второго члена (18), где появление sinα в точках α= 0 и α= π обращает поперечную силу в бесконечность.

Поэтому, чтобы исключить такую возможность, второй член в (18) приравняем к нулю. Такие особенности криволинейных координат проявляются в особых точках. Например, в круглых пластинах при интегрировании дифференциального уравнения равновесия постоянная интегрирования, обращающая в бесконечность поперечную силу в ее центре, также исключается [4].

Далее подстановка (18) в (11) дает

1 d M_a  N_a    sin a

^—^ — ^a-- :--N _р— q _Y= 0

R ² d a²     R a + R sin a ^{p Y}

Здесь потребовалось опустить производную д В     cos a

— = — a 2—, содержащую sin а в знаменате-да     sin a ле. Мембранные перемещения существенно мень- ше в сравнении с перемещениями нормальными к поверхности тора, поэтому не будем использовать уравнение (10).

Считая оболочку тонкой, в (13)–(14) уберем выражение в первой квадратной скобке, которая умножается на h ⁵, а в выражениях (15)-(16) пренебрежем квадратной скобкой при h ³. Тогда

M =   Eh³

^а   12(1 — ц ² )

n d ² w п Bi-тч + B 2 ^w ;

d а

Eh             Eh

N а =      2 B 3 w ,    N 3 =      2 B 4 w ;

(1 — ц )               (1 — ц )

ц ЕИ³

B 1 =, ¹ 12(1 — Ц 2 )

Выводы и результаты. Результаты расчета приведены на рис. 5–7. Дуга ABC верхней части тора показана распрямленной с конечно-разностной сеткой 200 узлов. Эпюра изгибающего момента М _a изображена на рис. 5. В точках А и С проявляется краевой эффект. На удалении от краев и в окрестности точки В обнаруживается практически безмоментное состояние.

Приведем вычисленные по формулам (21) мембранные силы N _a (рис. 6) и N в (рис. 7). В области, удаленной от краев, решения ожидаемые. Уравнение равновесия Лапласа для тора дает гра- ,                qR ( 2 a + R sin а )

фик усилия Nа =--2, который при- а    2 (a + R sin а)

веден на рис. 8. В точке В наблюдаем совпадение

Eh ³         ц a

12(1 — ц²) R ²( a + R sin а)’

B 3 =

Eh a + (1 + ц) R sin а (1 — ц²) R ( a + R sin а) ’

B 4 =

Eh ц a + (1 + ц) R sin а (1 — ц²)   R ( a + R sin а)

Пренебрежение в N _α и N _β членами при h ³ определяет, что в (21) эти усилия зависят не от производных функций прогибов, а только от функции прогиба. Подставив (20) и (21) в (19), получаем дифференциальное уравнение равновесия со старшей производной четвертого порядка.

Для численного решения задачи о деформировании тора преобразуем полученное дифференциальное уравнение в интегральное уравнение

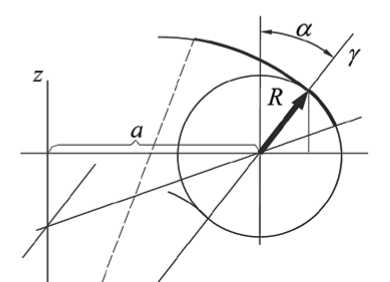
Рис. 3. Фрагмент тора в системе координат

s ₂

J B 1

^s 1 _

d2w d28w _ dw d§w ( B n ^ о , —2--— + B2--+1 — + B4 I w§ w ds + ds2 ds2 ds ds I R J

+

d ³ w      d ² w d § w    dw _

B1—3- § w + B1—2--+ B 2 —§ w + ds         ds ds      ds

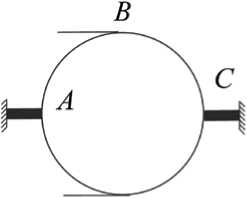
Рис. 4. Сечение тороидального бака, подкрепленного ребрами

+ B ₄ w § w

s ₁

s ₂

— J q Y§ wds = 0.

s ₁

В (22) оператор δ – оператор варьирования. Интегралы удобно вычислять по дуге s ( s = R a). Причем da = ds / R , d²M J d a² = R ²( d ² M J ds ²).

Составлена программа расчета тора вариационно-разностным методом [5], реализующая уравнение (22).

Расчет. Рассмотрим торовый бак, поперечное сечение которого изобразим на рис. 4. Бак закреплен по внутренней стороне (точка А ) и вдоль внешней кромки (точка С ). Верхняя часть тора обозначена точкой В . Примем R = 0,2 м, a = 3 R . Толщина стенки h = 5·10^–3 м. Модуль Юнга E = 2·10¹¹ Па; коэффициент Пуассона μ = 0,25.

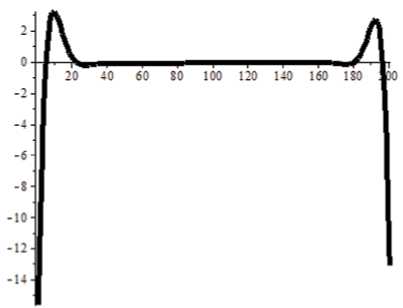
Рис. 5. Эпюра изгибающего момента M _α

результатов. На обоих графиках усилие одинаково qR и равно 20 000 Н/м. По формуле Nв = —, также полученной для безмоментного состояния, имеем результат 10 000 Н/м. Ровно такое же число Nβ (рис. 7) рассчитано в узле сетки 100.

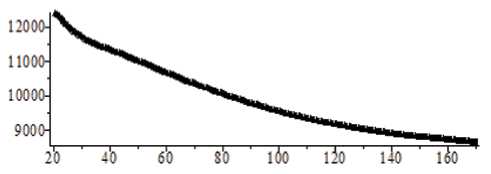
Рис. 7. Эпюра продольной силы N _β

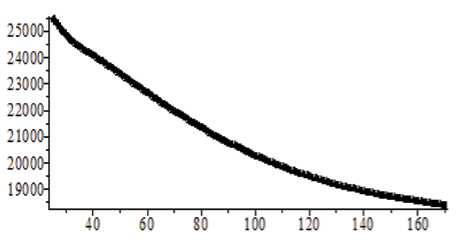
Рис. 6. Эпюра продольной силы N _α

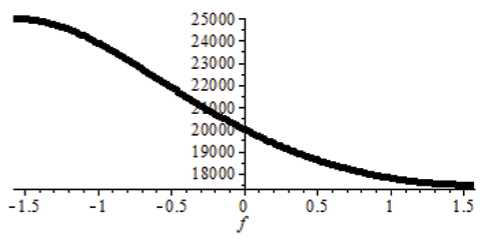
Рис. 8. Эпюра продольной силы N _а, полученная по безмоментной теории