Приложение вариационно-разностного метода к расчету продольно-поперечного изгиба пластин силами инерции

Введение. Элементы тонких пластин, используемые в военно-морских и аэронавигационных структурах, часто подвергаются нормальным и сдвигающим силам, действующим в плоскости пластин [1]. Решения проблем устойчивости имеют практические значения при конструировании ракет, высокоскоростных самолетов, подвергнутых значительным ускорениям [2]. Следует отметить возможность приложения этих решений для проектирования баннеров, тонких ограждений в виде вертикальных консольных пластин, находящихся под действием собственного веса. Поэтому можно заявлять об актуальности рассматриваемой темы.

Дифференциальная формулировка задачи устойчивости . Дифференциальная классическая формулировка задачи о продольно-поперечном изгибе изотропной пластинки в декартовой системе координат известна в литературе, она представлена уравнением равновесия [3]

„ Eh [au av Sxy —------I  + —

2(1 + ц) (a у a x

Функции перемещений для (2) могут быть вычислены с помощью уравнений равновесия Сен-Венана [5]:

a fa u a v ) 1 - ц fa ² u a ² u -----|--1--I +--| ----- 27 +-- 27 a x (a x a у ) 1+ ц ( a x ² a у ²

ЭД-ц q

Eh

D [^^w + 2

( dx 4

д ⁴ w a x²aу ²

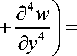
a² w      a ² w _ „ a² w

— N —7 + N —7 + 2 S --+ q , x a x ^{2      y} a у ²       x a x a у    z

в котором D — Eh ³/12(1 - ц²) - цилиндрическая жесткость; Е - модуль Юнга; ц - коэффициент Пуассона; h - толщина пластинки; w — w ( x , у ) - функция прогиба. Мембранные усилия N_x — N_x ( x , у ), N ^— N ⁽ x , у ), S x, ^— S x ,⁽ x , у ) правой части ⁽¹⁾ выра жаются через перемещения u — u ( x , у ), v — v ( x , у ) базисного слоя на основе закона Гука [4]:

N x —

Eh a u a v         Eh a v a u

--7 — + ц— , N_y —--2 — + ц— 1 - ц L a x a у J         1 - ц L a у a x

a fa u a v ) 1 - ц fa² v a ² v ) 2(1 - ц ) ...

—I— + —I + —-I—7 +—7 I — —-—— q. . (4) a у (a x a у J 1 + ц (a x ² a у ² J Eh

В (3), (4) для задач о действии ускор ений Q x ( x , у ) — hX , Q ( x , у ) — hY , 4 z ( x , у ) — 0, в которых объемные силы равны X — р a_x и Y — р а_у , зависят от плотности материала р и ускорений a_x , а_у по направлениям осей координат Ox и Оу соответственно.

Таким образом, сформирована система трех уравнений (1)-(4) относительно трех неизвестных функций u , v , w . К этим уравнениям добавляются статические и геометрические граничные условия. Отметим, что в уравнения (3) и (4) не входят прогибы; задача распадается на две: в первой задаче вычисляются функции u и v по формулам (3), (4), а во второй -определяются функции N_x — N_x ( x , у ), N_J — Nq, ( x , у ), S x _y — S xy ( x , у ) по формулам (2) и реализуется проблема собственных чисел, т. е. проблема расчета устойчивости пластины (1).

Обоснование предпочтения интегральной формулировки задачи устойчивости. Критерий устойчивости. При конечно-разностной аппроксимации дифференциальных уравнений (1), (3), (4), а именно, при рассмотрении свободных от закрепления углов пластинки, возникают алгоритмические трудности,

связанные с исключением законтурных узлов. Главной же особенностью является то, что аппроксимация вторых производных функций прогибов в (1) центральными конечными разностями дает несимметричную матрицу внутренних усилий, что затрудняет решение проблемы собственных чисел разрешающей дискретной краевой задачи. Этот факт явно прослеживается при формировании соответствующих матриц продольно-поперечного изгиба стержней [6]. Поэтому целесообразно к расчету пластин на устойчивость от действия сил инерции применить энергетические принципы. Здесь следует обратиться к основам теоретической механики и упомянуть теорему Лагранжа-Дирихле и Ляпунова, устанавливающую равновесие механической системы и определяющую критерии равновесных положений [7]. Для деформируемых конструкций, в частности для пластин, приложение энергетических принципов к проблеме устойчивости приводится в большом количестве научных разработок. Назовем здесь работы [1-5; 8-14], использующие как численные, так и аналитические методы расчета. Пусть

Э Л = Э Л ^{( w} i , ^w i ,---, w n ) ^{-                 (5)}

функционал Лагранжа конечного числа переменных w , , w , , ..., w_n краевой задачи. Приращение полной потенциальной энергии деформирования для вариаций w , + 5 w , , w ₂ + 5 w ₂,..., w_n + 5 w_n с удержанием членов не выше второго порядка имеет вид

А Э_Л = Э_Л ( w , + 5 w 1 , w ₂ + 5 w ₂,..., w n + 5 w n ) -

• -Эл (w„ w2,..., wK) = д Эл + 52Эл/2.(6)

Здесь первая и вторая вариации (5) соответственно равны

5Эл = (дЭл / дwk )5wk,(7)

• 52ЭЛ = (д2ЭЛ / дwkдwl)5wk5wl(8)

с суммированием по повторяющимся индексам: k = 1, 2, ..., к , l = 1, 2, ..., n . Для любого равновесного состояния 5Э_Л = 0 [8]. В задачах устойчивости о характере равновесия судят по знаку второй вариации функционала: устойчивое равновесие, если 5²Э_Л >  0 для всех допустимых виртуальных перемещений; неустойчивое равновесие, если хотя бы для одного допустимого виртуального перемещения 5²Э_Л <  0 . Но первая верхняя критическая нагрузка соответствует переходу от устойчивых равновесных положений к неустойчивым, следовательно, для этого значения нагрузки должно быть [10; 14; 15]

5²Э л = 0.                        (9)

Введем в (8) операторы варьирования 5 , и 5₂. Теперь запишем (9) так:

5²Э л = 5 2 (5₁Э л ( w„w ₂, ..., w n ;

5 1 w , ,5 , w ₂, ..., 5 , w n ; 5 2 w , ,5 2 w ₂, ..., 5 2 w_n )) = 0. (10)

Условие (9) с учетом (10) эквивалентно следующему уравнению

х

{ 5₂ w , 5₂ w ,

д ² Э

д w₁ д w , д ²Э л д w₁ д w ₂

д ²Э л д w₁ д w ₂ д ²Э л д w ₂ д w ₂

д ²Э л     д ²Э л

д wn д w,  д wn д w2

5₂ w , } х д ² Э л

д w1д wn

д ² Э л

^{д w}n ^{д w}n

I ^{5 w} , ] ⁵, ^w ,

⁵, ^w ,

= 0,

в котором, матрица n х n содержит коэффициенты при вариациях перемещений уравнения (10). Данная система будет иметь решение, отличное от нуля, лишь в том случае, если определитель, составленный из ее коэффициентов, равен нулю [10]. Группировка коэффициентов при независимых вариациях перемещений дает нулевой определитель

д 2Э л	д 2Э л	д 2 Э л	= 0.	(12)
д w1 д w , д 2Э л	д w 1 д w 2 д 2Э л	д w1 д wn ..           ...
д w 1 д w 2	д w 2 д w 2
... д Э	...             . д 2Э л	..           ... д 2 Э л
д wn д w ,	д wn д w 2	.  д wn д wn

Коэффициенты в (12) являются функциями параметров жесткости конструкции, соотношения ее размеров. Также они являются функциями внутренних усилий, зависящих в рассматриваемой работе от параметра ускорения. Параметр ускорения есть параметр нагрузки, который является единственной неизвестной характеристикой определителя (12); причем его значения, обращающие определитель в нуль, будут соответствовать критическим значениям нагрузки. Корни системы уравнений (12) определяют n собственных чисел, т. е. все критические нагрузки, в том числе наименьшую из них.

Преобразования дифференциальных уравнений плоской задачи теории упругости в интегральные уравнения. Используя основы вариационных принципов механики [13], дифференциальные постановки рассматриваемой задачи (1), (3), (4) заменим интегральными формулировками. В начале преобразуем уравнения (3) и (4). Для этого составим уравнение возможной работы внешних и внутренних сил

N + дSyx- + Xh 15 u + дx    дy      J

+

д S„,   д N

дx   дy

dxdy = 0,

из которого с учетом геометрических уравнений и закона Гука (2) для плоской задачи теории упругости, приемом интегрирования внутренних произведений по частям в прямоугольной области S : 0 <  x <  a и 0 <  y <  b получим:

- функционал Лагранжа:

^Ф л ⁽ u , v )

E

2(1 - Ц²)

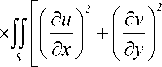
„ 6 и 6 v 1 - ц Г 6 и 6 v ) + 2ц — ■ / —+ — I

6 x 6 у   2 (6 у 6 x )

+ JJ ( Xu + Y v ) dx dy +

S

dxdy +

Для формирования коэффициентов жесткости a i j этой же системы уравнений составим вторую вариацию как вариацию первой вариации, реализуя (16) для дискретной задачи:

_6_Гу 6Ф Л (г7,5 1 11, 5 ₂г? ) к -1 6 и к ( i -1           6 и,

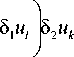
,                         x - a у - b

+ J (^xu + T‘xyv) dy у-0                     x-0

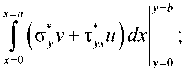
1, при к - i ;

0, при к ^ i ,

I 1, при l - j ;

5 1 и , - s [ 0, при l ^ j ,

- его вариацию

5Ф_Л - 5,Ф_Л   E— х

Л ¹ Л       (1 - ц²)

6 и 6 5 . v 6 v 6 5 . и |

1I + 6 x 6 у   6 у 6 x )

i - 1,2, ..., р ; j - 1,2, ..., р .

x JJ

S

6 и 6 5 . и 6 v 6 5 . v

---1----+ Ц

6 x 6 x   6 у 6 у

1 - ц (6 и 6 v |Г 65. и 65. v |

+^Я —+ — II -г1- + -г1- I

2 (6 у 6 x )( 6 у    6 x )

+ JJ ( X 5 и + Y 5 v ) dxdy +

S

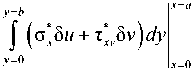
+ J ( g* 5v + тУx5и) dx x-0                        у-0

- и вторую вариацию функционала

5²Ф л - 5 2 (5 1 Э_Л) -- . E l | ^{(1 -}Ц )7

dxdy +

6 5 и 65. и

—2--— +

6 x 6 x

65, v 65. v Г 65, и 65. v 65. и 65, v ]

+ —²--— + ц | —²--— + —¹--— I +

6 у 6 у    ( 6 x 6 у    6 x 6 у )

1 - Ц Г 6 5₂ и + 6 5₂ v Y 6 5 1 и + 6 5 1 v

2 (6 у    6 x )( 6 у    6 x

dxdy .

Следует к (14)-(16) добавить главные граничные условия: и - и * , v - v * , 5_iu - 5 _iu * , 5 i v - 5 i v * , i - 1,2 (заданные значения отмечены символом «*»). В (14)(16) g x , т X _y , g * , т У _x - заданные напряжения.

Алгоритм формирования матриц жесткости и правых частей плоской задачи теории упругости в перемещениях. Таким образом, для решения краевой задачи (3), (4) вариационно-разностным методом применяем 5Ф Л - 5 1 Ф Л - 0 , что сообщает функционалу (14) минимальное значение. Рассмотрим приложение формул (15) и (16) для формирования системы разрешающих уравнений с целью вычисления перемещений и - и ( x , у ), v - v ( x , у ) пластины. Пусть и - ( и 1 , и ₂,..., и_р ) - вектор перемещений для р переменных, а 5 1 и - (5 1 и 1 ,5 1 и ₂,...,5 1 и_р ) и 5₂ и - (5₂ и 1 , 5₂ и ₂, ...,5₂ и_р )-вариации вектора перемещений. Тогда для вычисления коэффициентов b i вектора правой части системы разрешающих уравнений запишем (15) в виде

Е Р ^6Фл ^{( и} , ⁵1 ^и ) т --------------- 5. и

*

l -1        ^{6 и}1

i - 1,2, ..., р ;

I 1, при l - i ;

5 1 и , - s

[ 0, при l ^ i .

Решение сформированной системы уравнений a_ij1 l j - b i дает вектор перемещений и j , по компонентам которого вычисляются внутренние усилия N_x , У_у , S„, согласно (2). xy

Преобразования дифференциальных уравнений продольно-поперечного изгиба в интегральные уравнения. Для преобразования дифференциальной формулировки задачи (1) в интегральную формулировку воспользуемся уравнениями равновесия, полученными по деформируемой схеме в [3]:

⁶ Q x + ^{6 Q}y + N ^{6 2} w ^{( x} , у ) + N ^{6 2} w ^{( x} , у ) +

6x    6у     x   6x2       у6

+ ( ^ у + ^Syx ) ⁶ w ⁽ x , ^у ) + q_z ^{( x} , у )^{- 0} ,

'         '6

_п  6 м_х  6 H yx       6 М у 6

Q, -      +      ,  Q,. - у +

6x    6у          6у6

На основании (19) составим вариационное уравнение

JJ

s

62 Mx  62 Hyx  62 Hxy  62 Му6

-----;--1---1---1--;--+ Nx

6x2    6x 6у   6x 6у    6у2

6² w        _c \ 6² w

^{+ N}У "TT ^{+ ( S}xy ^{+ S}yx )УУ ⁺ q z

6 у    ^v          ' 6 x 6 у

5 wdS - 0,

где Mx - D (жх + ц$ ), M - D (ж + цжх ), H - H - x  xy yyxxyyx

^- ( 1 ^- Ц ) ^D X xy

ж

x

6 ² w

"йх2 ’

^ж у

изгибающие и крутящие моменты;

62 w ау7 ’

χ _xy

6 ² w

6 x 6 у ’

У, - 6 w / 6 x , x

Э _у -6 w / 6 у - кривизны кривой линии и углы поворота; 5 w ( x , у ) - возможное перемещение базисной по

верхности пластины; dS - dxdy . Считая внутренние

силы N_x , N_)J , S_xy известными функциями, выполнив процедуры интегрирования внутренних произведений в интеграле (20) по частям, получим вариационное уравнение

x - а у - b

^5ЭЛ ^- J J D [ ^ж x ^5ж x ⁺ Ц ^(ж x ^5ж у ^{+ ж} у ^5ж x ) ^{+ ж} у ^5ж у ⁺ x -0 у -0

x - а у - b

+ 2 (1 - Ц) X xy 5X xy ] dxdy - J J qz 5 wdxdy - x-0 у-о

,x у - b

-J( Rx 5 w - Mx 5Sx) dy- у-0

- J (Ry 5w - My 5Sy) dx x=0

+ (Я + ЯJ6wlx=a |y=b + x xy yx/ lx=0l x = a y=b

+ J J ( N x S x 5 S x + N_y S _y5 S y + S xy ( S y 5 S x + S x 5 S y ) ) dxdy - x =0 y =0

-J( NxSx + SxySy) 6 wdy- y=0

x = a

-J( SyxSx + NySy) 5 wdx   = 0,(21)

x=0

где 5 - оператор варьирования; R_x = Q_x + d H_xy 1 5 y , R_y = Q_y + d H_yx I d x - реакции. Из (21) следуют функционал Лагранжа

1 x=a y=b

Э Л ^х J J D ^Г$^{2 + 2ц} ® x $ y ⁺ $^{2 + 2} ( 1 ^{- Ц} ) X x ] ^dx dy ^-

² x =0 y =0

J

,                            ,x

У = bУ

J qwdxdy-J (Rxw-Mx»,)dy y=0               У=0

x=a

-J( RyW - MySy ) dx    ■ ( H  ■ Hyx ) W|x =0 |y = 0 + x=0

। x = a y = b

+ 7 J J ( N S + N y S y ² + 2 S xy S y S x ) dxdy -

² x =0 y =0

- J(NxSx + SxySy) wdy y=0                           x=0

- J( SyxSx + NySy) wdx x=0                            y =0

и вторая вариация этого функционала

6²Э = = = D Г б $ 5 $ + ц(5 $ 5 $ + 5 $ 5 $ ) + J!                   |              2 x 1 x * ' 2 x 1 y 2 y 1 x *

x =0 y =0

+ 52$ у 51$ у + 2 (1 - И ) 52X xy 51X xy ] dxdy + x = a y=b

+ J J( Nx 52Sx 5S + Ny 52Sy 5Д + x=0 y=0

+ S xy (5 2 S y 5 Д + 5 2 S x 5 Д ) ) dxdy ,        (23)

где 5 i , i = 1, 2, - операторы варьирования;

, „     d25 i w	. „      d25 i w	.         d2 5 i w
5 ^$                 , i x       d x x	i $ y       d y 2 ,	5 i X xy d x d y

5 i S _x = d 5 i w I d x , 5 i S _y = d 5 i wI d y - вариации кривизны линий и вариации углов поворота.

Формирование матриц жесткости и матриц внутренних усилий проблемы устойчивости. На основании (9) выражение (23) приравняем к нулю, что приводит к постановке задачи устойчивости дискретной задачи. Пусть w = (w1,w2, ...,wp) - вектор перемещений для p переменных, а 51 tw = (51 w1, 51 w2, ...,51 wp) и 52-w = (52w1,52w2, ...,52wp) - вариации вектора перемещений. Сформируем для дискретной задачи систему (12) подобно (18):

^5 _df y д Э_Л ( >w , 5 1 tw , 5₂ - w ) k =1 dtw _k ( i =1           dtw ,

⁵1 w l P 2 w k = ⁰ ,

_ I 1, при k = i ;

5 2 w_k = S

[0, при k * i, i = 1, 2, ..., p ;

_     1 1, при l = j ;

5 1 w l = S

[ 0, при l * j, j = 1, 2, ..., p .

Здесь каждый коэффициент C j = B ij - sA ij , согласно (23), содержит характеристики жесткости ( A ij ) и внутренних усилий ( B ij ); s - корни уравнения (12). Умножив найденные из (24) C ij на вектор w j , получим C j w j = 0,                    (25)

что представляет формулировку обобщенной проблемы собственных значений

[ B ] { w } = s [ A ] { w } ,                 (26)

где [ B ] назовем матрицей внутренних усилий; [ A ] -матрица жесткости; { w } = ( w 1 , w ₂, ..., w_p ) - собственный вектор для p переменных; s - собственные числа.

Дискретизация дифференциальных операторов конечно-разностными аналогами и аппроксимация континуальной области сеточной. Выполним дискретизацию уравнений (15), (16), (23). Выберем на области пластинки прямоугольную равномерную сетку Юу ={(x = iXx, yj = jXy), i = 0,1,...,m, j = 0,1, ...,n} на отрезках [0, lx ] и [0, ly ]. Здесь x = xi и y = yj -узлы сетки; X, = / I m и X„ = L, I n - шаг сетки, а L xx    yy          x и ly - размеры пластинки по направлениям осей координат x и y. Эту сетку (рис. 1) с узлами i, j назовем основной сеткой. Введем дополнительную сетку с узлами ^, П: Ю^п ={( x 5 = X xI2 + iX x, yj = X y I2 + jX y X i = 0, 1,...,m-1, j = 0, 1, ...,n-1}. Интегралы по области в (15) и (16) и второй интеграл от внутренних усилий в (23) заменим численным интегрированием JJ( )dxdy = £^2( )S«п (здесь S- площадка S                    «=1 п=1

интегрирования, равная X _x X _y во внутренних узлах области пластины), а дифференциальные операторы заменим конечно-разностными аналогами [16]:

Г d 5 k u ^   = ⁵ k u i +1, j +1 ^{+ 5} k u i +1, j ^{- 5} k u i , j +1 ^{- 5} k u i , j

I dx J5,n "                  2 Xx’

Г d 5 k V ) = ⁵ k v i +1, j +1 ^{+ 5} k v i , j +1 ^{- 5} k v i +1, j ^{- 5} k v i , j

Idy J "                 2X„,

V x k «,п

Г d 5 k U ₊ d 5 k V ) = ⁵ k^ui +1, j +1 ^{+ 5} k^ui , j +1 ^{- 5} k^ui +1, j ^{- 5} k^ui , j ₊

I dy     dx L

«,п vk it+1,j +1 1 ^k^i +1,j ^k^i,j+1 vk it,j

I

2X _x

Далее, в первом интеграле (23) интегрирование для членов, содержащих вариации кривизны   δkæx и δkæy, заменим суммированием по узлам основной mn сетки JJ( )dxdy = ^^( )Sij и применим централь-S                      i=1 j =1

ные разности. Здесь площадки интегрирования S_{i , j} равны: λ _x λ _y – во внутренних узлах области пластины; λ _x λ _y /2 – в узлах, расположенных на контуре; λ _x λ _y /4 – в узлах, расположенных в углах пластинки:

f d 2 5 k w ) = 8 k w i+1,j ^- 25 k w i,j + 5 k w i-1,j

I dx2  J.  "               X2

i,j f d25kw) = 5kwi,j+i - 25kwi,j + 5kw,j—1

I  dy2  Ji,j=                X2•

Кривизну кручения δ _k χ _xy вычислим в узлах типа ξ, j :

f d 2 5 k w J = ⁵ k w i +1, j +i ^{- 5} k u i , j +i + ⁵ k u i,j —1 ^{- 5} k u i +1, j

6x 5y J

ξ,j и в узлах типа i, η:

f d 2 5 k w )   = ⁵ k w i +1, j +1 ^{- 5} k u i —1, j +1 + ⁵ k u i-1,j ^{- 5} k u i +1, j

[ dxdy j. "                   2X.X,.

i,η

Здесь k = 1,2.

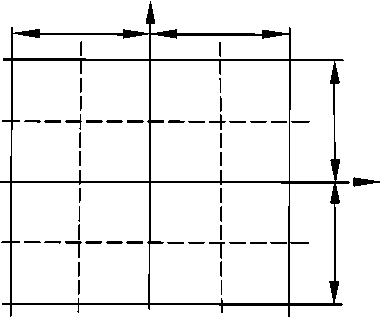
Рис. 1. Конечно-разностная сетка: сплошными линиями обозначены линии основной сетки; штриховыми линиями обозначены линии дополнительной сетки

Примеры расчета. Для расчета продольнопоперечного изгиба тонких пластин используем математический пакет Maple [17], позволяющий вычислять собственные числа и собственные значения матриц. Приведем два примера расчета устойчивости от сил инерции.

Пример 1. Пластина жестко защемлена по всему контуру; объемные силы равны X = рax = 1 и Y = рay = 0 . Размеры в плане: lx = 0,8 м; ly = 0,6 м; толщина h = 0,01 м. Материал пластинки имеет характеристики жесткости: E = 1010 Па и р = 0,45 . Плотность материала р = 3 г/см3. Пусть допускаемое ускорение [a] равно 50 g.

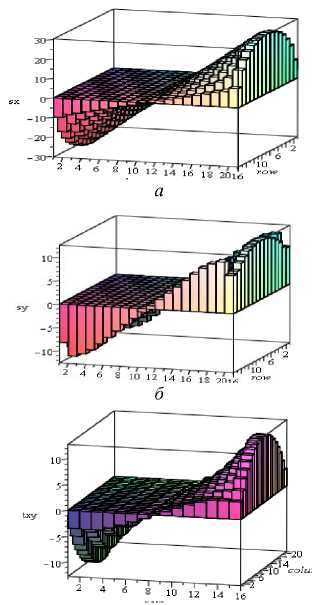
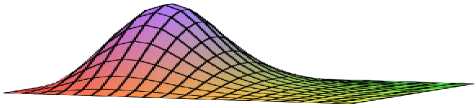
Первый этап расчета включает в себя вычисление внутренних мембранных усилий (2), эпюры которых приведены на рис. 2. По найденным перемещениям базисной поверхности пластины (рис. 3) построим ее деформированный вид (рис. 3, а ). Решение обобщенной проблемы собственных значений (26) (это второй этап расчета) представляет первая форма поперечного изгиба (рис. 3, б ).

в

Рис. 2. Эпюры внутренних усилий: а – продольные N_x ; б – продольные N_y ; в – сдвиговые S_xy (размерность внутренних усилий Н/м)

б

Рис. 3. Деформированный вид поверхности пластины: а – перемещения линии сетки срединного слоя; б – выпучивание – первая равновесная форма

Инерционная нагрузка здесь такова, что формируемая матрица внутренних усилий имеет на главной диагонали нули и эта матрица не имеет обратной мат- рицы.

Найдем ускорение, отвечающее первому собст- венному значению, равному 304 Н/м3: ax

304 ^ρ

304 = iooo м/с². Ускорение слишком велико 3 - 10 - ³

и, видимо, близко к ударным нагрузкам. Заключаем, что заданная пластина не потеряет устойчивость, так как полученное критическое ускорение, равное 100 g , меньше допускаемого [ a ] = 50 g .

Пример 2 . В качестве второго примера рассмотрим пластину, закрепленную только с одного торца, когда три других края свободны и не закреплены. В ее плоскости действует постоянное ускорение. Аналогичная задача расчета продольно-поперечного изгиба была приведена в [2], где изучалось действие на вертикальную консольную пластинку постоянного ускорения; для решения задачи применен метод Ритца.

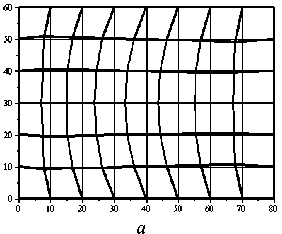
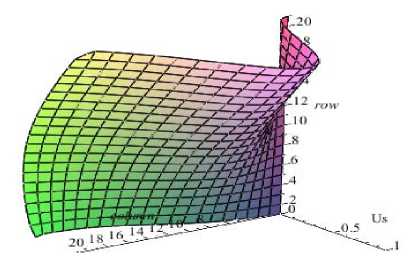
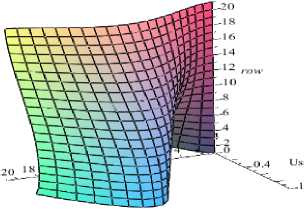
Пластина имеет размеры в плане 0,6×0,8 м и толщину 0,1·10^–3 м; модуль Юнга материала равен 2·10¹¹ Па; коэффициент Пуассона –0,25; плотность 780 кг/м³. Ускорение a y (это параметр) направлено по оси абсцисс. Требуется определить критические ускорения. На рис. 4 отображен деформированный вид, полученный на первом этапе решении задачи до возникновения критических ускорений. На рис. 5 приведен вид функций внутренних мембранных усилий, приводящих к потере устойчивости. На рис. 6 продемонстрированы полученные формы потери устойчивости пластины, там же отмечены четыре первых критических ускорения, соответствующих этим формам. Таким образом, чтобы достичь при разгоне ускорения, равного, к примеру, 41 м/с², следует не допустить предыдущих критических ускорений 30 и 40 м/с². Следует обратить внимание, что система Maple первое и четвертое собственные числа подобрала отрицательными и выдала соответствующие им формы (рис. 6, а , г ) в противоположном направлении. На первый взгляд, отрицательное значение собственного числа противоречит критерию потери устойчивости, что если минимальное собственное значение положительно, тогда конструкция устойчива. Здесь рассматривалась обобщенная проблема [ A ] { w } = 5 * [ B ] { w } ( 5* = 1/ 5 ). Если всегда [ A ] >  0, тогда больше нуля должно быть произведение 5 * [ B ] >  0 , а не собственное значение 5 * .

Дополнительно отметим в этой задаче особенность приложения вариационно-разностного подхода. На свободных краях пластины при формировании матриц жесткости записывались уравнения равновесия как в узлах на контуре, так и в законтурных узлах, поэтому размерности сформированных матриц [ A] и [B] в (26) не совпадали. Дополнительные уравнения о равенстве нулю изгибающих моментов и обобщенных реакций на контуре понижали размерность матрицы [A] до размерности матрицы [B]. Эти дополнительные процедуры сложения соответствующих строк между собой и столбцов матриц были автоматизированы для сеток различной густоты, что несколько усложняло общий алгоритм. Реализация же дифференциальной формулировки задачи (1) методом конечных разностей для пластины со свободными краями затруднительна.

б

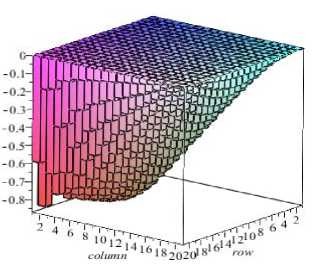
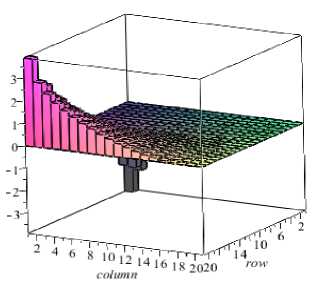
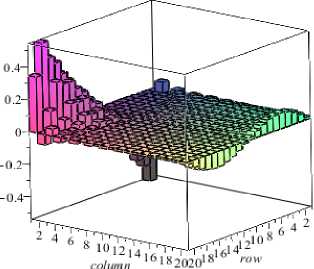
Рис. 5. Пространственный вид эпюр внутренних усилий: а – N_x ; б – N_y ; в – S_xy

а

в

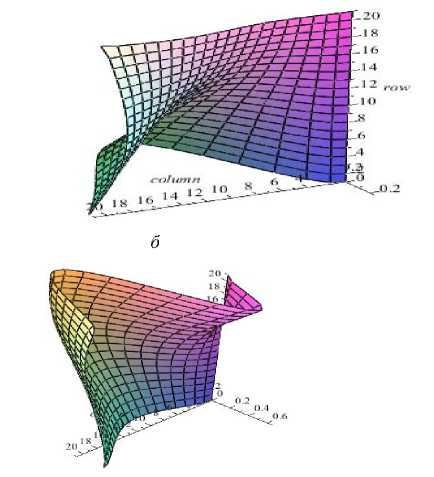
Рис. 6. Формы потери устойчивости при ускорениях: a – –29 м/с²; б – 30 м/с²; в – 40 м/с²; г – –43,3 м/с²

Заключение. Таким образом, рассмотренный подход к расчету пластин может быть использован для подбора и анализа геометрических и параметров жесткости панелей при заданном ускорении или торможении, применяемых в аэрокосмической технике.

Матрица жесткости и матрицы внутренних усилий формировались с помощью прикладной программы интерпретатора Maple, что ограничило возможности сгущения конечно-разностной сетки и численного решения задачи большой размерности, исследования сходимости результатов. Поэтому для дальнейших исследований желательно использование пакетов программ, основанных на алгоритмических языках высокого уровня.

Необходимо сказать, что на поиск всего спектра собственных чисел и форм программа Maple затрачивала на два порядка больше времени, по сравнению с временем формирования матриц с применением предложенных здесь методов. Для обеспечения достоверности был применен метод скалярных произведений, позволяющий вычислять максимальное собственное число. Однако это требовало вычисления обратной матрицы жесткости, тогда как матрицы внутренних усилий обратных матриц не имели.