Приложения биноминального распределения в биологических задачах

На сегодняшний день без математических методов не сможет обойтись ни одно элементарное исследование. В области ветеринарной медицины и экспертизы математику используют очень многогранно и широко. В пример можно привести такие математические методы, как построение научных теорий, обработка и анализ результатов эксперимента [1, 2, 4, 6].

Быстрые темпы развития современного естествознания за несколько десятилетий позволили изменить полностью физическую картину мира, что помогло ветеринарии достигнуть большого прогресса. Одним из факторов ускоренного развития науки, занимающейся профилактикой, диагностикой и лечением болезней животных, оказалась математика.

В задачу математики и математической статистики входят классификация и систематизация данных. Данный подход позволяет ускорять развитие отраслей животноводства, а в ветеринарии использовать математический анализ для моделирования течения болезней.

В математической статистике есть раздел, изучающий случайные события и случайные величины, а также их свойства и операции над ними, и он называется теорией вероятности [3, 5].

Если опыт, в котором появляется событие А , имеется конечное число n равновозможных исходов, то вероятность события А равна

P ( A ) = ^m , (1)

n где m - число благоприятных исходов, n - число всех возможных исходов.

Теория вероятности используется при анализе крови. По капле крови с помощью данной теории и математических исследований можно определить общее физиологическое состояние животного (рисунок 1).

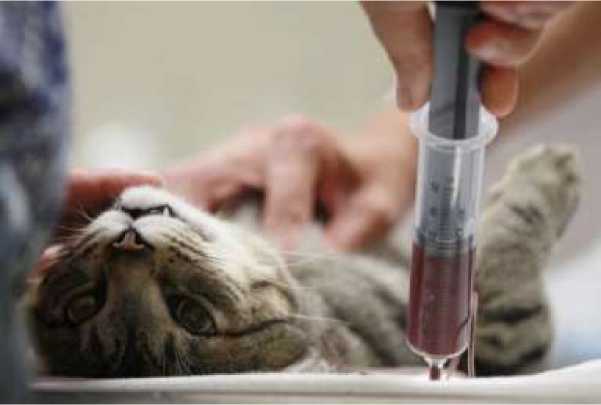
Рисунок 1 - Взятие крови у кошки на анализ уровня креатинина

В теории вероятностей есть раздел, изучающий распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна p , который называется биноминальное распределение.

Рассмотрим задачу из генетики. Пусть отношение полов равно 1:1 и пол новорожденного не зависит от пола детей, родившихся в семье до него. Какова при этом вероятность того, что в семье с тремя детьми будут две девочки и один мальчик? Ответить на этот вопрос нетрудно, но стоит рассмотреть его подробнее в качестве примера более сложных задач того же класса (рисунок 2).

Рисунок 2 - Две девочки и один мальчик

Прежде всего зададимся вопросом: какова вероятность некоторой определенной семьи с мальчиком и двумя девочками, взятой с учетом последовательности рождения детей, например, мальчик-девочка-девочка. Ответ ясен

111 1

— . — . — = —

.

222 8

А сколько может быть разных типов семей с разной последовательно- стью рождения одного мальчика и двух девочек?

Ответ также очевиден:

- мальчик-девочка-девочка;

- девочка-мальчик-девочка;

- девочка-девочка-мальчик.

Итого три типа.

Значит вероятность того, что в семье с тремя детьми будет один маль- чик и две девочки, равна

3 • ¹ =

.

Это пример так называемого биноминального распределения.

Прежде чем излагать его в общем виде, рассмотрим более сложный пример. При скрещивании белой кошки и серого кота в F1 (гибриды первого поколения, полученные от скрещивания двух родительских типов) все котята будут серыми, а в F2 (гибриды второго поколения, полученные от скре- щивания гибридов из F1 ) «математическое ожидание» белых котят будет равно ,

т. е. в потомстве от большого числа таких скрещиваний на трех се- рых котят будет приходиться один белый (рисунок 3).

Пусть у нас имеется один помет F ₂ из пяти котят. Тогда какова вероятность того, что три котенка будут серыми, а два белыми?

Рисунок 3 - Белая кошка и серый кот

Как и в предыдущем случае, мы сначала рассчитываем вероятность какого-либо определенного помета расчетом последовательности рождений, например, помета, в котором два котенка белые, а остальные серые. Представим эту схему в табличном виде (таблица).

Таблица - Последовательность рождения котят разного окраса

Порядковый номер	1	2	3	4	5
Окрас котенка	Белый	белый	Серый	серый	серый

Вероятность того, что первые два котенка будут белыми равна

= —.

4 416

а того, что последующие три котенка будут серыми, равна

3 3 327

— . — . — —--

.

4 4 464

Итак, вероятность такого сочетания окраса котят в помете равна

(1)ч3 )’

V 4 7 V 4 7

« 0,026 .

Теперь нужно определить, сколько существует типов пометов, с уче- том последовательности рождений, в которых два котенка белые, а остальные серые. Эта задача эквивалентна следующей: «Сколькими способами из пяти номеров можно выбрать два, соответствующих двум белым котятам?»

Первый номер может быть выбран пятью способами, и, поскольку один номер уже выбран, для выбора второго остается четыре возможности. Казалось бы, это означает, что существует 5^4 = 20 типов пометов, содержащих по двое белых котят. Однако это не так.

Среди этих 20 типов мы помет каждого типа сосчитали дважды: помет, в котором оба первых котенка белые, мы сначала сосчитали как помет, в котором сперва был выбран первый номер, а потом второй, а затем - как помет, в котором сначала был выбран второй номер, а потом первый.

То же самое относится и ко всем остальным типам помета, например, к схеме «белый-серый-серый-серый-белый».

Таким образом, общее число типов пометов равно

¹ ■ 5 ■ 4 = 10 .

Правильность полученного результата можно проверить, перебрав все возможные типы пометов.

Итак, вероятность того, что в помете будет два белых котёнка и три серых, равна

10 ■

(17 (3 У

.     ■ 7V 4 7 V 4 7

« 0,264 .

Заметим, что этот результат также можно записать в виде

5! ■f 1 7 2!3! V 4 7

гV47

где 5! означает 1-2-3^5 и читается как «пять факториал».

Обобщая полученный результат, можно сформулировать следующую теорему: если вероятность события равна p, то вероятность того, что это событие произойдет m раз в последовательности n независимых испы- таний, равна n!        m        n - m

P =-- P ' ( 1 - P )     .                   (2)

m ! • ( n - m )!

Или, введя, как обычно, обозначение q = 1 - p , можно сформулировать эту теорему в следующей форме: если вероятность события равна p, то вероятности того, что в последовательности n независимых испытаний оно произойдет 0, 1, 2, …, m , …, n раз, задаются последовательными членами многочлена ( q + p ) ⁿ , т. e.

n    n-1   n(n -1) n-2 2        n!      n - m m      n q ,nq  p,—-— q   p ,-••         q p ,-, p .

2              m!(n - m )!

Мы не будем приводить формального доказательства этой теоремы. Оно аналогично ходу рассуждений в только что рассмотренном частном случае на примере рождения котят двух окрасов.

Так, вероятность того, что первые m испытаний из n будут успешны-m      n - m ми, а остальные неудачными, равна p (1 - p)   , а число возможных спо собов выбрать m объектов (т. е. «удачных» испытаний) из n возможных (об- щего числа испытаний) равно

n !

m !( n - m )!

С помощью этой биноминальной теоремы можно рассчитывать вероятность семьи любого типа.

Существует еще один прием часто применяемый при расчете вероятностей. Предположим, например, что нам надо рассчитать вероятность того, что в результате скрещиваний белой кошки и серого кота в помете F 2 , содержащем восемь котят, по крайней мере один будет белым. Можно, конечно, рассчитать вероятности пометов с 1, 2, 3, …, 8 белыми котятами и затем сложить их. Но это очень громоздко, и, к счастью, в этом нет необходимости. Оказывается, достаточно вычислить вероятность того, что в помете не будет ни одного белого котенка,

P (0)= 3V 4 7

« 0,1001 ,

и вычесть ее из единицы, поскольку вероятность того, что в помете будет по крайней мере один белый котенок, равна

P (хотя бы один) = 1 - Р (0) ~ 0,8999.

Другими словами, если рассчитать вероятность какого-либо события трудно, то можно попытаться рассчитать вероятность того, что это событие не произойдет. А затем из единицы вычесть полученный результат.

Таким образом, можно сделать вывод о том, что между ветеринарией и математикой существует очень разносторонняя связь. И в даже в таких, казалось бы, очень далеких от математики областях, как анатомия животных, генетика, микробиология, эпизоотология, гистология, эмбриология и радиобиология используются методы вероятностного анализа.