Применение адаптивного регрессионного моделирования для описания функционирования технического объекта

Требование безаварийного функционирования любого технического объекта является актуальной задачей. Для этого проводится регулярный контроль определенных показателей качества, причем значения входных и выходных параметров опре-деляются по результатам измерений в режиме реального времени. Традиционно для оценки качества работы объекта используется набор показателей, имеющих определенный физический смысл (технические, физические, химические и т.д.). В работе рассматривается объект, который характеризуется набором р параметров х 1 - х р , среди которых можно выделить k управляемых факторов х p-k +1 - х p . Измерялись также m показателей качества функционирования объекта y 1 - y m . Требовалось исследовать влияние регрессоров х 1 - х р на отклики y 1 - ^{y m .} Для построения математической модели описанного объекта при р = 8, k = 2, m = 7 был применен подход адаптивного регрессионного моделирования, подразумевающий исследование и выбор оптимальных методов. По совокупности имеющихся данных за год для каждого отклика y ₁- y 7 были построены и исследованы модели. Для расчетов использовался пакет Statistica [5]. Модели, полученные методом наименьших квад-ратов, характеризовались наличием незначимых параметров и эффектом мультиколлинеарности [1, 2]. Поэтому были исследованы возможности применения ряда методов адаптации к выявленным нарушениям основных предпосылок применения регрессионного анализа.

Для моделирования показателей качества объекта были получены регрессии с использованием выборок размером 30, 60, 100 дней и по ним произведены прогнозы на 2-4 следующих дня. Предлагаемые размеры выборки можно объяснить

тем, что при разделении исходного файла на выборки пришлось учитывать неизменность физикохимических показателей объекта в течение достаточно продолжительного времени. В частности, один из управляемых параметров изменяется в диапазоне от 0,12 до 0,22, и периоды неизменных значений могут быть от нескольких дней до сотни суток (за исследуемый период максимальное значение 113 дней). Известно, что наличие в обрабатываемом файле столбца из одинаковых значений при компьютерной обработке данных приводит к возникновению ошибки и остановке расчета. Ниже в качестве примера приведены модели множественной регрессии для откликов y ₁, y ₆ полученные для выборок разного размера, а также значения коэффициента детерминации R ².

Для годовой выборки:

y 1 = 22,93 + 0,02 x 1 + 0,45 x 2 – 0,02 x 3 – 0,97 x 4 + +1,11 x 5 - 0,003 x 6 - 3,73 x 7 – 6,2x 8 ; R ²= 0,16.

y 6 = 6,8 – 0,0003 x 1 + 0,13 x 2 – 0,008 x 3 – 0,18 x 4 – 0,06 x 5 + 0,18 x 6 – 1,24 x 7 – 1,78x 8 ; R ²= 0,35.

Для выборки из 100 наблюдений:

y 1 = 13,91 - 0,34 х 1 + 0,77 х 2 – 0,13 х 3 +0,21 х 4 + 1,19 х 5 + 0,26 х 6 – 6,66 х 7 + 31,95 х 8 ; R ²= 0,29

y 6 = –3,23 + 0,14 х 1 – 0,07 х 2 – 0,04 х 3 –0,41 х 4 + 0,70 х 5 + 0,11 х 6 + 1,34 х 7 + 2,48 х 8 ; R ²= 0,5.

Для выборки из 60 наблюдений:

y 1 = - 8,68 + 1,17 x 1 - 0,09 x 2 – 0,19 x 3 – 1,48 x 4 + 4,35 x 5 -0,01 x 6 + 2,71 x 7 + 29,43x 8 ; R ²= 0,44.

y = –6,87 – 0,01 х – 0,3 х – 0,01 х – 1,25 х + 1,00 х + 0⁶,15 х 6 –^, 3,87 х 7 ^,+ 1,¹72 х 8 ^,; R ²²=0,7^,.   ^{3    ,    4    ,    5}

Для выборки из 30 наблюдений:

y 1 = -282,8 + 2,32 x 1 - 7,97 x 2 – 0,09 x 3 – 1,81 x 4 + 0,77 x 5 - 0,085 x 6 + 83,25 x 7 – 39,34x 8 ; R ²= 0,31.

y 6 = 9,5 – 0,024 х 1 – 0,27 х 2 – 0,003 х 3 + 0,05 х 4 + 0,27 х 5 + 0,003 х 6 – 2,83 х 7 + 2,46 х 8 ; R ²= 0,67.

Были получены модели множественной регрессии для всех откликов y1-y7, которые являются показателями качества функционирования рассматриваемого объекта. Анализируя полученные модели для каждого отклика с учетом разного размера выборки можно говорить о неустойчивости полученных моделей в пространстве параметров. Об этом свидетельствует достаточно большой разброс оценок параметров по разным выборкам, в том числе и смена знака. Для оценки качества полученных по выборкам моделей были использованы такие статистики (меры качества) как стандартная ошибка σΔ , коэффициент детерминации R2, об-щий F-критерий. Так как значения этих статистик получаются путем обработки данных, на основе которых строится модель, то они являются внутренними критериями. Данные меры для каждой из исследуемых моделей приведены в табл. 1.

Таблица 1. Внутренние меры качества моделей

Отклик	Объем выборки	R 2	F-критерий	Стандартная ошибка	Кол-во значимых регрессоров
y 1	30	0,31	1,16	0,73	1
	60	0,44	4,88	0,8	0
	100	0,29	4,54	0,89	0
	годовая	0,16	8,2	0,91	2
y 2	30	0,11	0,34	0,03	0
	60	0,47	5,57	0,02	2
	100	0,44	9,1	0,03	2
	годовая	0,28	16,22	0,04	3
y 3	30	0,25	0,8	0,05	0
	60	0,14	1,05	0,06	0
	100	0,18	2,5	0,06	1
	годовая	0,33	20,64	0,08	3
y 4	30	0,59	3,76	18,82	2
	60	0,49	5,74	15,99	3
	100	0,52	12,55	12,7	3
	годовая	0,12	6,19	20,99	5
y 5	30	0,15	0,47	0,06	0
	60	0,19	1,51	0,06	1
	100	0,15	2,03	0,06	1
	годовая	0,47	37,59	0,06	1
y 6	30	0,67	5,24	0,16	2
	60	0,7	15,25	0,2	2
	100	0,5	11,71	0,22	1
	годовая	0,35	23,09	0,3	1
y 7	30	0,35	1,41	0,02	1
	60	0,39	3,98	0,02	3
	100	0,31	5,07	0,02	3
	годовая	0,42	30,82	0,02	6

Анализируя полученные модели для всех откликов y ₁- y ₇ по внутренним мерам качества, можно сделать вывод, что размер выборки в 60 наблюдений является наиболее предпочтительным для построения прогноза.

Исследование корреляционной матрицы показало, что между регрессорами х1 и х3, х1 и х8, х2 и х7 существует сильная линейная взаимосвязь. Это явление называется мультиколлинеарностью и имеет весьма отрицательные последствия для оценивания коэффициентов регрессии [1]. Следует также отметить, что отклик y4 связан корреляционной связью средней силы с х7, а отклик y6 с регрессором х6. В табл. 2 приведены коэффициенты парной корреляции между параметрами x1-x8 и откликами y1-y7 (набором показателей качества технического объекта).

Анализ остатков, полученных для моделей по 60 наблюдениям, показали, что для каждого из откликов существуют выбросы (значения, выходящие за стандартное отклонение остатков). В табл. 3 приведен список выбросов, обнаруженных при построении моделей для каждого из откликов.

Таблица 2. Коэффициенты парной корреляции

	y 1	y 2	y 3	y 4	y 5	y 6	y 7
1	2	3	4	5	6	7	8
x 1	0,09	-0,13	-0,45	-0,15	-0,67	0,18	-0,48
x 2	0,25	0,40	0,09	0,14	0,45	0,13	0,31
x 3	-0,05	0,04	-0,16	0,11	-0,14	-0,03	-0,18
x 4	-0,04	0,11	0,06	-0,17	-0,16	0,12	-0,19

1	2	3	4	5	6	7	8
x 5	0,08	0,12	0,17	0,05	0,26	0,01	0,52
x 6	0,10	0,30	0,04	-0,18	-0,17	0,57	0,01
x 7	0,24	0,39	0,09	0,14	0,46	0,12	0,32
x 8	-0,09	0,15	0,40	0,14	0,66	-0,18	0,44

Таблица 3. Выявленные выбросы (аномальные наблюдения) для откликов

Отклик	Наблюдения с зафиксированными выбросами	Количество выбросов
y 1	42	1
y 2	14, 21, 26, 51	4
y 3	-	-
y 4	4, 27	2
y 5	9, 12, 36	3
y 6	19, 54	2
y 7	9, 28, 42	3

Distribution of Raw residuals

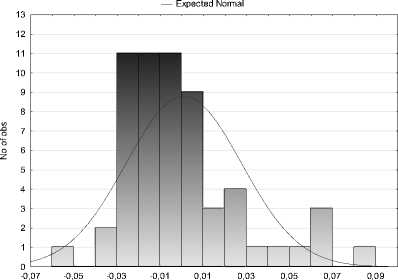
-0,06     -0,04     -0,02      0,00      0,02      0,04      0,06      0,08      0,10

Рис. 1. Гистограмма остатков для отклика y ₂

Distribution of Raw residuals

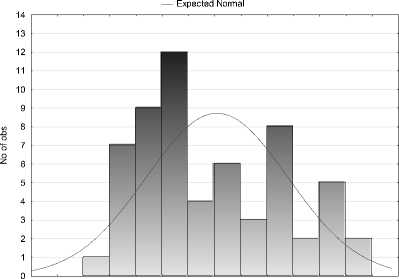
-0,14 -0,12 -0,10 -0,08 -0,06 -0,04 -0,02 0,00 0,02 0,04 0,06 0,08 0,10 0,12 0,14

Рис. 2. Гистограмма остатков для отклика y 3

На рис. 1 и 2 приведены гистограммы остатков для откликов y 2 и y 3 , которые позволяют сделать вывод о нарушении предположения регрессионного анализа о нормальности распределения остатков. Приведенные гистограммы остатков для исследуемых моделей получены с использованием пакета Statistica [5].

Для контроля рассматриваемого объекта с целью регулирования его параметров необходима модель, содержащая управляемые параметры х7 и х8. Рассматривая в совокупности полученные меры качества моделей, и учитывая выявленные нарушения условий МНК, далее предложены некоторые методы адаптации [4, 6, 7]. Для преодоления выявленных нарушений был использован метод пошаговой регрессии. Пошаговая множественная регрессия является статистическим методом аннализа связи между зависимой переменной (y) и множеством независимых переменных (x1,x2,…,xp) и осуществляет отбор независимых переменных в порядке их значимости. Критерий значимости основывается на уменьшении сумм квадратов. Независимая переменная, наиболее влияющая на это уменьшение на данном шаге, вводится в регрессию. Одним из существенных элементов данной реализации является добавление в алгоритм операции исключения регрессора, включенного в модель на данном шаге и ухудшающего значение критерия, по которому производится поиск оптимальной модели.

Далее для анализа был применен метод случайного поиска с адаптацией и случайного поиска с возвратом. Задачу поиска оптимального набора регрессоров можно рассматривать как задачу оптимизации функционалов с булевыми переменными zj ( j = 1, p ) , равными 0 или 1. Методы пошаговой регрессии и случайного поиска с адаптацией позволили получить модели со значимыми параметрами и хорошими прогностическими свойствами, но не все из них содержат необходимые управляемые параметры х 7 и х 8 . Значение коэффициента детерминации (0,67) в соответствии с принятой шкалой соответствует «заметной» силе связи. В состав моделей входит от 2 до 6 параметров объекта, при этом не во все модели вошли оба управляемых параметра х 7 и х 8 . Если не использовать принудительное введение этих параметров, то подходящей модели по методу пошаговой регрессии, как и по МНК, не получено. Гребневое оценивание позволило получить модели с малыми значениями коэффициента детерминации и F-критерия, что не соответствует требованиям оптимальной модели. Результаты расчетов методом пошаговой регрессии и гребневого оценивания приведены в табл. 4. В ней приводятся номера параметров, вошедшие в модель, полученную пошаговым методом и внутренние меры качества для каждого из примененных методов.

Таблица 4. Меры качества модели при пошаговом и гребневом оценивании

От кл ик	Пошаговая регрессия				Гребневая регрессия
	№ параметра	R 2	F -критерий	cтандарт ная ошибка	R 2	F- критерий	cтандарт ная ошибка
y 1	1, 2, 3, 5	0,42	10,08	0,82	0,4	4,28	0,86
y 2	2, 5, 6, 7, 8	0,47	9,22	0,03	0,36	3,53	0,03
y 3	3, 5, 7	0,13	2,9	0,06	0,13	0,9	0,05
y 4	2, 3, 5, 6, 7, 8	0,47	9,56	15,6	0,27	2,33	18,9
y 5	1, 2, 7, 8	0,18	2,9	0,05	0,15	1,1	0,06
y 6	2, 3, 4, 5, 6, 7	0,7	20,95	0,2	0,7	12,69	0,21
y 7	2, 5, 7	0,28	7,0	0,2	0,3	2,6	0,02

При использовании метода случайного поиска с адаптацией, были получены модели, характеризующиеся небольшой стандартной ошибкой, сравнимой по значениям с результатами множественной и пошаговой регрессии. По коэффициенту детерминации и F -критерию получено небольшое улучшение качества модели. Основным достоинством данных моделей можно считать тот факт, что каждая из них содержит управляемые параметры х 7 и х 8 , которые необходимы для регулирования состояния технического объекта.

При исследовании влияния объема выборки на характеристики полученных моделей, используя только внутренние меры качества, был выбран наиболее предпочтительный объем, равный 60 измерениям. Анализ корреляционных связей между параметрами модели и показателями качества рассматриваемого технического объекта позволил выявить существенные взаимосвязи, которые требуют дальнейшего исследования. При исследовании остатков полученных моделей были зафиксированы аномальные наблюдения, которые требуется исклюю-чить из исходных данных при дальнейшей обработке. Методы пошаговой регрессии и случайного поиска с адаптацией дали модели с хорошими прогностическими способностями, но не полностью соответствующие заявленным требованиям.

Дальнейшие исследования предполагают получение моделей с максимально возможным набором параметров по выборкам объемом 60 наблюдений. Выбор наилучшей для прогноза модели предполагает использование различных мер качества моделей, как внутренних, так и внешних. Для адаптации к выявленным нарушениям планируется использовать также методы гребневого и робастного оценивания.