Применение алгоритма Дейкстры в сфере сервиса

Алгоритм получил своё название от фамилии своего выдающегося создателя: Эдсгера Ви́бе Де́йкстра - знаменитого нидерландского ученого, в свою очередь, внесшего огромный вклад в развитие информационных технологий и самой информатики. Его научные достижения в области применения математической логики при разработке программ принесли ему немалую известность. Он является одним из тех ученых, кто превратил программирование в науку.

Помимо всего этого, ему принадлежит идея алгоритма нахождения кратчайшего пути, предложенная им еще в 1952 году. Этот алгоритм появился в процессе работы Дейкстры в одном из Математических центров, когда он занимался задачами по оценке производительности компьютера ARCMAC. Благодаря данному алгоритму ученый мог найти наилучшие решения для определения оптимального пути передачи электрического тока наиболее важным элементам цепи, тем самым минимизируя расход меди. Он назвал этот способ «алгоритм древа с кратчайшими ветвями». Успешно используя данный алгоритм, Дейкстра решает его оформить и придать всемирной огласке в 1959 году.

Данный алгоритм получил ни одну область применения, он имеет широкое использование не только в сфере информатики и программирования. Задачу поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог, применяют при планировании автомобильных и авиа-маршрутов. В сфере сервиса алгоритм Дейкстры используется, например, в логистических операциях. При наличии всей необходимой информации с помощью данного алгоритма можно, например, узнать какую последовательность дорог лучше использовать, чтобы добраться из одного города в другой, или в какие страны выгодней экспортировать тот или иной продукт. Алгоритм широко применяется в программировании и различных технологиях, например, его используют протоколы маршрутизации OSPF.

Прямой задачей алгоритма является нахождение кратчайшего пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Рёбрами или дугами графа могут быть как стоимость перевозки товара из одного города в другой, так и длина переводки, или же диаметр трубы. То есть важно, что бы ребра в алгоритме Дейкстры не были отрицательными. Алгоритм поможет найти все кратчайшие пути из одной, изначально заданной, вершины графа до всех остальных. Работает пошагово, на каждом последующем шаге посещается одна из вершин. Недостаток данного алгоритма лишь в том, что он будет некорректно работать, если граф имеет дуги отрицательного веса.

Начало алгоритма инициализация: Допустим, дан ориентированный граф, на его ребрах записаны некоторые числа. Обозначим точку отправления - вершина 1, путь из неё, в неё же равен 0. Метки остальных вершин отметим символом «бесконечность», как показано на рисунке 1, это показывает то, что расстояние от точки отправления до других вершин пока еще не известно.

Рис. 1 Инициализация алгоритма.            Рис. 2 Граф с отмеченной мин.

Шаг алгоритма: Точку отправления 1 помечаем буквой Z – это означает, что она отмечена как «минимальная метка», из неё передвигаемся к соседним вершинам и узнаем длину пути (Рис. 2).

Узнав и сравнив все длины, отмечаем вершину Z как посещенную. Далее выбираем наименьшую и обозначаем как следующую «минимальную метку» Z. Из этой вершины происходят последующие расчеты до соседних вершин, иначе говоря, данный шаг алгоритма повторяется, пока мы не посетим все вершины. «Сосед» вершины 3 — вершина 2, если идти в неё через 3, то длина такого пути будет равна 50 (10 + 40 = 50). Но текущая метка второй вершины равна 30, а это меньше 50, поэтому метка не меняется (Рис. 3).

На рисунке 4 показан граф, когда все его вершины посещены и алгоритм завершен. Исходя, из рисунка 4 можно сделать вывод, что кратчайший путь из вершины 1 до 2 – 30, до 3 – 10, до 4 – 45, до 5 – 20, до 6 – 55.

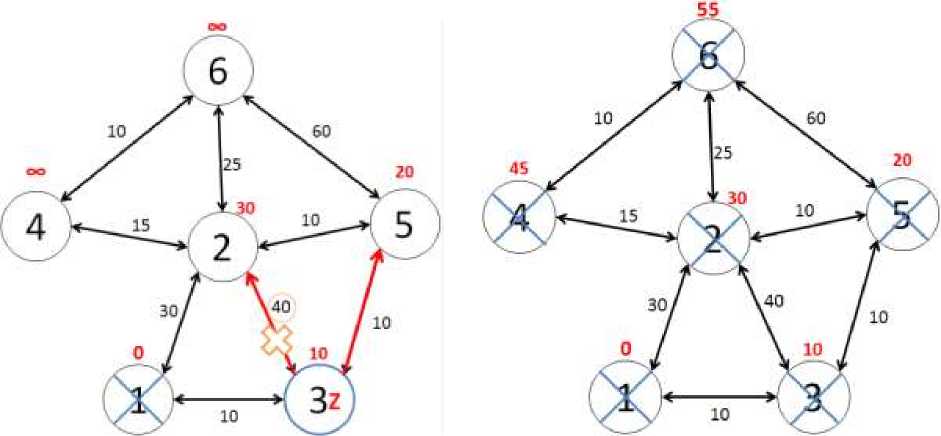
Рис. 3 Неизменность метки.

Рис 4. Завершение алгоритма.

Используя алгоритм, помимо логистических задач доставки товаров, можно организовывать выставочную деятельность. Главная задача организаторов выставки сделать участие максимально удобным и эффективным как для экспонентов, в том числе для представителей многочисленных зарубежных компаний, так и для посетителей. Из-за того что выставочные залы, зачастую, имеют не идеальную и/или витиеватую форму, необходимо сделать так, чтобы каждый посетитель пройдя один раз по залу, смог ознакомиться со всеми экспонатами выставки, и ни один из них не повторился.

Специфическим способом расстановки товаров пользуются и торговые сети. Иногда, что бы приобрести хлеб, необходимо пройти длинный путь, до самого дальнего отдела магазина. То есть, разместив продукты, пользующиеся наибольшим спросом (молоко, мясо, хлеб и т.п.), в разных отделах магазина, можно отвлечь покупателя от его изначального списка покупок и попутно притягивать его внимание яркими вывесками "АКЦИЯ" или "СКИДКА". В итоге, на выходе потребитель уносит в своей сумке, товары, которых даже не было в перечне покупок.

Каждый человек ежедневно, не всегда осознавая это, решает проблему: как снизить затраты, в условии ограниченных ресурсов. Применение Алгоритма Декстры несомненно полезно во всех сферах человеческой деятельности. Руководствуясь им в достижении цели можно выбрать оптимальный курс развития, повысить эффективность продаж, минимизировать затраты и не только. Алгоритм имеет преимущество в том, что легко может быть положен в основу программы, которая имеет небольшой размер. Применение программы значительно упростит использование алгоритма.