Применение CAD / CAE технологий для исследования работоспособности элластичного обтюратора в условиях импульсного нагружения высоким давлением

Одной из основных причин разгарно-эрозионного действия при работе газодинамических импульсных устройств (ГИУ) является прорыв газов между трубой и обтюрирующими устройствами изделия. Практика работы газодинамических импульсных устройств показы- вает, что появление прорыва газов вызывает повышенный износ трубы ГИУ на том участке, где имеет место прорыв. При значительном износе происходит недопустимое уменьшение максимального давления газов и начальной скорости изделия.

В процессе проектирования ГИУ проводится тщательная экспериментальная отработка обтюрирующих устройств изделий, которая требует учета множества взаимосвязанных факторов, происходящих в сложных напряженных условиях их функционирования. В настоящее время в качестве эксперимента прежде всего предпочтение отдают численному эксперименту, проводимому на базе популярных CAD/CAE систем, таких как Autodesk, SolidWorks, Ansys и др.[1].

Популярность этих пакетов для решения задач оценки функционирования изделий в сложных динамических условиях обусловлена предоставляемой ими возможностью средств (собственных баз и решателей), обеспечивающих возможность исследования линейных и нелинейных процессов, в том числе происходящих в средах с различными физическими свойствами. При этом задача исследователя заключается в определении границ расчетных областей с использованием САD системы, в выборе уравнения состояния - модели поведения материалов с различными свойствами в различных условиях, выборе подходящего решателя и определения граничных для расчетной области и начальных условий для происходящих в ней процессов.

Процесс функционирования обтюрирующих устройств происходит в условиях высокой динамики нагружения и высоких давлений. При этом элементы обтюрирующих устройств, как правило, изготавливаемые из полиамидных гиперупругих материалов, испытывают конечные пластические деформации - изменяют форму в процессе выполнения своей функции при относительно высокой скорости деформирования. Для описания процессов деформирования и разрушения в подобных условиях применяют различные физические модели, учитывающие условия нагружения и поведение сплошной деформируемой среды в этих усло-виях[2]. К возможным для данного случая следует отнести модель Ми-Грюнайзена, учитывающую динамику процесса, а также модели Муни-Ривлина, Нео-гука и Огдена, применяемые традиционно для гиперупругих материалов, испытывающих конечные деформации и высокие скорости деформирования и объемные давления. В данной статье оценивается применимость моделиМи-Грюнайзена [3] дополненной уравнением вязкопластичного поведения материала - уравнением Купера-Саймондса[4] и Муни-Ривлена [3, 4].

Структура модели Ми-Грюнайзена такова, что правая часть, уравнения состояния состоит из двух слагаемых, первое из них соот- ветствует потенциальному давлению и зависит только от изменения объёма, второе обусловлено динамической составляющей процесса -колебаниями кристаллической решётки и пропорционально энергии этих колебаний е:

Г где P - давление, РП( V) - потенциальное давление, e - внутренняя энергия, e0(V) - внутренняя энергия при начальном объёме, V - объём, Г -коэффициент Грюнайзена, характеризующий тепловое давление со стороны колеблющихся атомов.

Г(V ) = V I P ! . v ^{d e} ) V

При низких температурах вклад второго слагаемого в полное давление мал, и уравнение состояния в основном определяется первым членом - потенциальным давлением. С ростом температуры роль теплового давления возрастает. Оно может сравняться с потенциальным давлением и даже превзойти его. В этих условиях значением потенциального давления пренебрегают, и вместо него в расчёт принимается зависимость теплового давления от объёма.

Если учитывать, что деформирование обтюрирующих элементов при функционировании ГИУ носит ударно-волновой характер, тогда, для определения уравнения состояния необходимо применить уравнение ударной адиабаты Гюгонио с определением коэффициента Грюнайзена [1]:

где U S - скорость ударного фронта; U 1 - массовая скорость ударно-сжатого вещества; С -скорость звука в веществе перед фронтом; S -показатель адиабаты:

.

Здесь Г - коэффициент Грюнайзена, характеризующий тепловое давление со стороны колеблющихся атомов.

Адиабатическое движение деформиру- емых упругопластических сред описывается следующей системой уравнений:

P^U = 0; Р U = ^^ ; рdE = се dt            dt d Р + dt

dD

- e5 ij) =

q — — d5 - - 4" D - - . X — —~ ij       p ii       ^g ij ,        2y2

^G «4 ,     (5)

Она описывает как линейную, так и объёмную деформацию; С 1 и С ₂ константы материала, связанные с модулем сдвига, обеспечивающие минимальное отклонение кривых истинных напряжений от кривых напряжений полученных экспериментально.

где p - плотностьвещества; V - дифференциальный оператор Гамильтона; U - компонент вектора скорости; о, - компонент тензора

,

напряжений; в_у - компонент тензора скоростей деформаций; E - энергия единицы массы вещества; D - компонент девиатора напряжений; G - модуль сдвига; Я ' - некоторый множитель, учитывающий динамическую составляющую сжимаемого вещества; G -метрические коэффициенты основного базиса системы координат; p - давление; V - объём; Y - динамический предел текучести; 5_у - функция Кронеке

д W _

Для несжимаемых материалов д11

д W

= C ; 11, 12 - главные инварианты деви- д12

атора деформаций; 1 1 , 1 ₂ - главные инварианты деформации Коши-Грина, J - детерминант

матрицы

градиента

деформации,

- коэффициент несжимаемости

материала, р = 0,49 - коэффициент Пуассона для эластомеров, G - модуль сдвига.

Инварианты деформаци Коши-Грина:

I = U2 + U2 + Uз2;

ра.

Система уравнений (5) включает дифференциальные уравнения законов сохранения массы импульса, энерги, а также физические и

I = U ²и² +и²и² +и²и²- ;

кинематические уравнения, связывающее внешние нагрузки с компонентами напряжений и деформаций [2].

Уравнение Купера-Саймондса дополняют систему (5) путем учетареологического

где

U 1 , U ₂, U ₃ - главные значения тензора де-

упрочненияпутем учета зависимости предела текучести от скорости деформации:

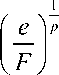
Здесь: с₀ = 92 МПа - статический предел текучести; e - мгновеннаяскорость деформации (в начальный момент времени в = 1); B, F,p - константы материала: B =40,08 МПа - модуль упрочнения; F =1 , p =0,001 - коэффициенты Купера-Саймондса.

В модели Муни-Ривлина учитываются свойства эластомеров испытывать относительно большие конечные деформации за счёт перераспределения объёма, т.е. эти материалы считаются практически несжимаемыми с коэффициентом Пуассона близким к 0,5 [4,5]. Основной характеристикой модели Муни-Ривлена определяется функция плотности энергии деформации. Общая и широко используемая форма функция плотности потенциальной энергии деформации W была предложена Ривлином [6]:

формаций. При I ₃ = 1 материал считается несжимаемым.

Напряжения в материале:

„ SW-   QW- - 1

^G j =^{- р 5} j ^{+ 2} h;¹- ^{- 2}       ■⁽⁸⁾

Особенностью модели Муни-Ривлена является возможность определения реальных свойств эластомеров с любой степенью точности путем сопоставления расчетных и экспериментальных значений компонент НДС при подборе коэффициентов модели. Это является значимым основанием для ее широкого применения при расчете изделий, изготавливаемых из эластомеров.

Далее приведена сравнительная оценка НДС обтюрирующего устройства, выполненного из полимерного материала с использованием моделей Ми-Грюнайзена и Муни-Ривлина. Моделирование проводилось в программном пакете ANSYS с использованием решателя Autodyn в явных Лагранжевых координатах. Задача решалась в осесимметричной постановке. На рисунке 1 представлен общий вид расчетной модели.

На рисунке 2 представлена схема приложения граничных условий.Граничными условиями решения задачи в обоих случаях определены следующие:

• -    перемещения изделия, заданы соответствующими положению изделия в различные моменты времени в соответствии с кривой (рисунок 4);

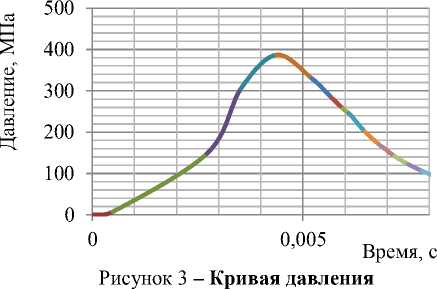
• -    давление газов p на запоясковую часть изделия, переменное во времени в соответствии с кривой изображённой на рисунке 3.

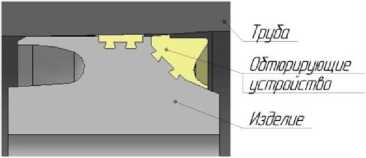
Рисунок 1 – Общий вид геометрической модели экспериментальной зависимости σ–ε (рисунок 5).

Полное ограничение

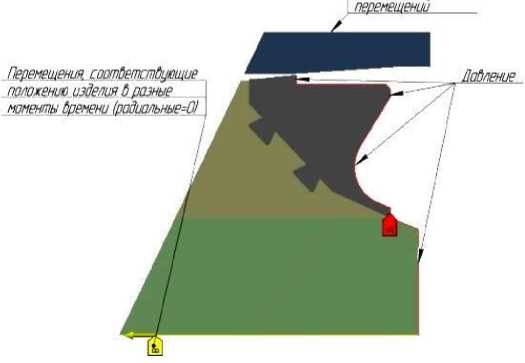
Рисунок 2 – Схема приложения граничных условий

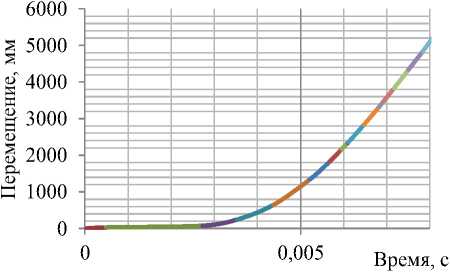
Рисунок 4 – Перемещение изделия в различные моменты времени

В качестве физических моделей с, учётом особенностей моделей материалов программного пакета Аnsys, определены:

• -    для трубы ГИУ – идеальной упругости.

• -    для изделия – Ильюшина А.А. (малой упругого-пластической деформации с линейным упрочнением);

• -    для обтюрирующего устройства (полиамид) – двух параметрическая модель Муни-Ривлина и уравнение состояния Ми-Грюнайзена (таблица 1).

Определение коэффициентов модели Муни-Ривлена производилась на основаниии

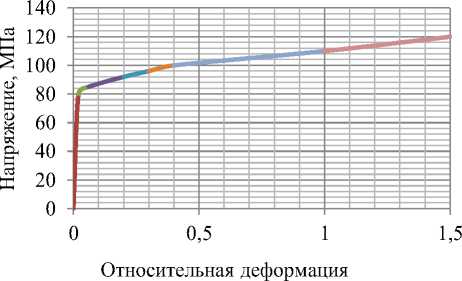
Рисунок 5 – Зависимость напряжений от деформации с линейным упрочнением для полиамида

Таблица 1 – Механические свойства полиамида

Модель	Ro , кгс/м3	µ	σt, МПа	G, МПа	K Г	С , м/с	S	C 1 , МПа	C 2 , МПа	D , 1/МПа
Ми-Грюнайзена	1100	0,49	92	533,6	0,87	2620	1,63	-	-	-
Муни-Ривлина	1100	0,49	92	533,6	-	-	-	-37,176	147	0,00194

*Здесь: Ro – плотность материала, µ – коэффициент Пуассона, G –модуль сдвига, К_Г– коэффициент Грюнайзена, С – скорость звука, S –показатель адиабаты, С ₁ и С ₂ – постоянные материала, D – параметр несжимаемости.

Результаты расчета проиллюстрированы картинами напряжений и деформаций, со- ответствующих времени максимального давления для моделей Ми-Грюнайзена и Муни-Ривлина (см. рисунки 6 - 7).

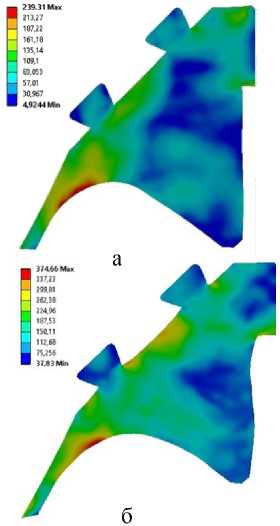
Рисунок 6 - Интенсивность напряжений обтюрирующего устройства при максимальном давлении (МПа):а - модель Ми-Грюнайзена; б -модель Муни-Ривлина

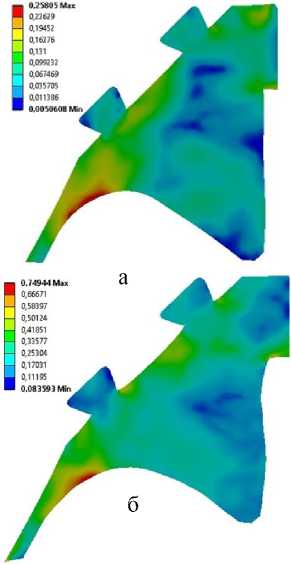
Рисунок 7- Интенсивность деформаций обтюрирующего устройства при максимальном давлении: а - модель Ми-Грюнайзена; б - модель Муни-Ривлина

Из результатов расчётов видно, что при прочих равных условиях, для модели Муни-

Ривлена при максимальном значении интенсивности напряжений 374 МПа максимальная деформация составляет порядка 74 %., в то время как для модели Ми-Грюнайзена при максимальном значении интенсивности напряжений 239 МПа максимальная деформация составляет порядка 25 %. Для того, чтобы выяснить причину расхождения расчётов был проведён ряд численных экспериментов по сжатию цилиндрических образцов полиамидного материала c разной скоростью деформации (рисунок 8) с использованием модели Муни-Ривлина и Ми-Грюнайзена.

Моделирование, проводилось в программном пакете ANSYS с использованием решателя Autodyn в осесимметричной постановке. Механические свойства материала соответствовали таблице 1.

Граничные условия деформирования определялись получением скоростей деформации, сопоставимых со скоростями деформации обтюрирующих устройств, при работе ГИУ.

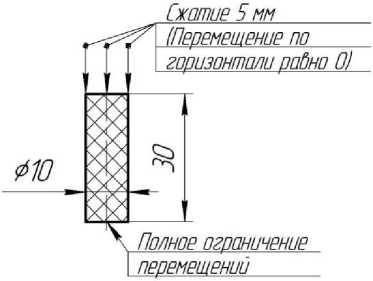
Рисунок 8 - Схема приложения граничных условий образца

На рисунке 9 представлены сравнительные зависимости интенсивности напряжений от скорости деформации, полученные в результате сжатия образцов.

Из результатовследует, что напряжения, полученные с использованием модели Ми-Грюнайзена и Муни-Ривлина различаются. Причем очевидным является влияние динамики нагружения, выраженное постепенным увеличением напряжений по модели Ми-Грюнайзена при росте скорости деформации на участке до 2000 с-1 вследствие учитываемых реологических свойств материала. Далее, при увеличении скорости деформирования,напряжения, полученные с использованием модели Ми-Грюнайзена резко увеличиваются, что, очевидно, объясняется влиянием ударно-волновых процессов, также учитываемыхв модели Ми-Грюнайзена.Этим и следует объяснить существенную разницу в результатах значений НДС обтюрирующих устройств, приведённых на рисунках 6 и 7.

Таким образом, очевидно, что при оценке напряжённо деформированного состояния обтюрирующих устройств, работающих в условиях высоких скоростей нагружения, необ- ходимо учитывать влияние динамики процесса деформирования. Критическим значением для полиамидных устройств следует принять значение скорости деформации 2000 с-1, определяемое величиной форсирования и скоростью прохождении изделия по трубе.

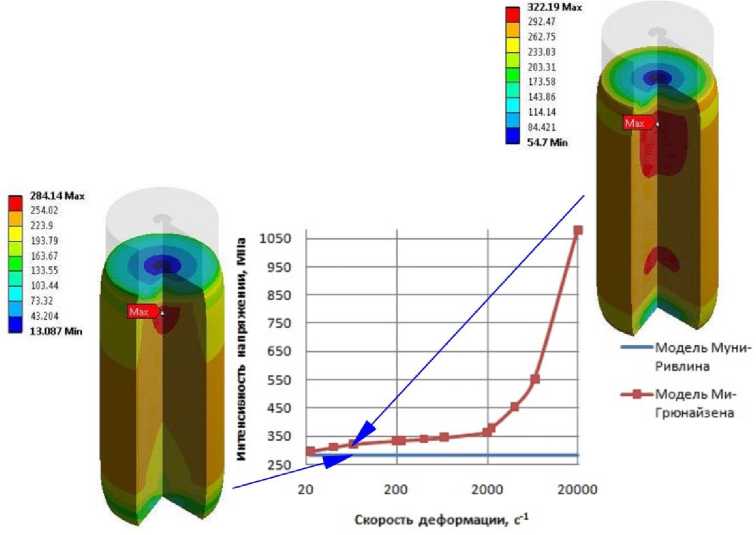
Рисунок 9 – Диаграмма зависимости интенсивности напряжений (МПа) от скорости деформации

Выводы

Проведен сравнительный анализ функционирования обтюрирующих устройств ГИУ, изготовленных из полиамида, с применением для расчета НДС моделей Ми-Грюнайзена и Муни-Ривлена. В результате получены значительные расхождения результатов расчетом с использованием данных моделей. Проведенные дополнительные численные исследования показали значительное влияние на НДС динамики нагружения, учитываемой уравнением состояния Ми-Грюнайзена с учетом вязкопластичного поведения материала в соответствии с уравнением Купера-Саймондса, имеющего различный характер при скоростях деформирования до и более 2000 с-1). На основании того, что реальные условия деформирования обтюрирующих устройств происходят в условиях, когда скорости деформации могут достигать значенийв несколько десятков и сотен с-1 расчеты для них целесообразно проводить с моделью Ми-Грюнайзена с учетом влияния скорости деформации на пластическое течение материала, например по уравнению Купера-Саймондса.