Применение численных фундаментальных решений в методе точечных источников поля

Введение. Метод точечных источников поля (МТИ) является одним из эффективных методов моделирования физических полей (например, электрических и магнитных) в технических (в том числе электромеханических) устройствах [1–4]. Для указанного метода характерна высокая точность численного решения и чрезвычайная простота ком- пьютерной реализации [5–9]. Наилучшие результаты получены при использовании МТИ для моделирования физических полей, описываемых однородными линейными уравнениями эллиптического типа с известными фундаментальными решениями, задаваемыми аналитически. Такими уравнениями являются уравнение Лапласа, уравнение Гельмгольца, бигармоническое уравнения, некоторые другие типы уравнений. Применение МТИ в этом случае позволило решить значительное число прикладных задач по моделированию, например: стационарных электрических, магнитных [8–10], тепловых, концентрационных полей [11–14], полей упругих напряжений [15–17]. МТИ успешно применяется также при численном решении краевых задач для неоднородных уравнений, таких как уравнение Пуассона [18– 19], неоднородное уравнение Гельмгольца [19–21]. Однако во всех случаях использования МТИ предполагается известным фундаментальное решение соответствующего уравнения математической физики. Это резко ограничивает круг решаемых с помощью МТИ задач. Тем не менее, и в этом случае возможно решение краевых задач с помощью МТИ, если предварительно найти численные значения фундаментальных решений при определенных значениях параметров. Назовем фундаментальное решение, заданное численно, численным фундаментальным решением (ЧФР). Ниже описан метод нахождения ЧФР для линейных уравнений эллиптического типа и показывается возможность использования этих решений в МТИ.

Интегральное уравнение для дополнительной составляющей фундаментального решения. Пусть фундаментальное решение g ( r ) линейного уравнения эллиптического типа LU = 0 известно. Требуется найти фундаментальное решение G ( r ) уравнения типа ( L + l ) U = 0 . Здесь L и l — линейные операторы эллиптического типа. Представим искомое фундаментальное решение G ( r ) в виде

G ( r ) = g ( r ) + u ( r ) .                                                        (1)

Здесь u ( r ) — искомая функция. Назовем g ( r ) основной составляющей, а u ( r ) — дополнительной составляющей фундаментального решения G ( r ) .

В соответствии с определением фундаментального решения справедливо соотношение ( L + l ) G = 5 ( r ) .

Подставим в это выражение (1). В результате получим

(L +1)(g + u) = 5(r), или                                              Lg + Lu + lg+ lu = 5 (r).                                               (2)

Так как Lg = 5 ( r ) ( g ( r ) есть фундаментальное решение уравнения LU = 0 ), то уравнение (2) запишем в виде Lu = - lg - lu .                                                        (3)

Правую часть этого уравнения будем рассматривать как плотность заряда р (r) неоднородного уравнения Lu = р (r). Тогда частное решение неоднородного уравнения (3) можно записать в виде u (r ) = J g (r, R) P (R) d Q R или в виде u (r)+J g(r,R)lu (R)dQr = -Jg(r,R)lg(R)dQr .                                   (4)

Q                  Q

Областью интегрирования в (4) может быть шар радиусом R 0 , который заключает в себя область ω задачи, решаемой с помощью искомого фундаментального решения.

Уравнение (4) допускает численное решение. В результате находятся приближенные значения для ЧФР в узловых точках области Q ^ ю. Эти значения можно использовать при решении задачи Дирихле с помощью, например, МТИ. При решении задачи Неймана или краевой задачи третьего рода наряду со значениями фундаментального решения необходимо иметь возможность вычисления нормальных производных фундаментального решения на границе области ω или частных производных по координатам. Для вычисления частных производных можно воспользоваться соотношением (4). Например, продифференцировав (4) по координате x, получим d u(r\      8 g(r, R it’-J^r21 < u (R)+g (R)) dQ r.                           (5)

О x      q    о x

Аналогичное соотношение можно получить для частной производной дополнительной составляющей фундаментального решения по координате y и по координате z (при решении трехмерных задач). Используя найденные значения функции u ( r ) в узлах области Q с помощью численного интегрирования в правой части соотношения (5) можно вычислить приближенные значения частной производной дополнительной составляющей фундаментального решения в любой точке области Ω и использовать эти значения при численном решении краевой задачи.

Фундаментальные решения уравнения Шредингера. В качестве простейшего примера найдем фундаментальные решения одномерного уравнения Шредингера, описывающего колебания квантового осциллятора. Пусть частица массой m совершает упругие колебания с частотой ω и энергией Е . Уравнение Шредингера запишем в виде [22]

d ² ψ2 mm ² ω ²

—т +  EV = —'< v , dx2   й2         h2

mω а после замены переменных x^~x "^ x запишем как d2ψ2

+   Ev = x V, или как dx2  йю d2ψ        2

—- + e v = x v, dx ²

где e - —E . йю d2

Здесь операторами L и 1 , фигурирующими в (2)-(4), будем считать L - —- и 1 = - x ² . Как известно, фунда- dx ²

d ²_V                             sin (V e|x |)

ментальное решение уравнения + eу = 0 равно g(x)----^—;=—- [23]. Классически допустимая область движе- dx2                            2 e ния осциллятора ограничивается отрезком [-Ve, Ve ], поэтому в качестве области решения для квантового осциллято ра можно взять отрезок ю = 1-Ve,Ve|=[-1, 1], а областью интегрирования в (4) считать, например, отрезок

Q = [-1,5 Ve, 1,5Ve ] = [-d, d] . Тогда уравнение (4) запишется как u (x)—-^= J sin(Ve|x - X I) X 2 u (X) dX -^- J sin (Ve|x - X|)sin(Ve|XI)X2dX .

Обозначим интеграл в правой части интегрального уравнения (7) как f ( x ). В данном случае функция f ( x ) вычисляется аналитически. В более общем случае, если исходное дифференциальное уравнение имеет другой вид, функцию f ( x ) находят численно.

Для численного решения уравнения (7) интеграл в левой части соотношения (7) представляют в виде интегральной суммы, используя тот или иной метод численного интегрирования. Если, например, используется простейший метод численного интегрирования, метод прямоугольников, то отрезок Ω разбивается на N элементарных отрезков.

Обозначим значения искомой функции u (x) в некоторых, например, в средних точках xi элементарных отрезков как ui, где i — номер элементарного отрезка. В результате для величин ui, будет получена система линейных алгебраических уравнений вида f 1,                          i - j;

¹ a j u , - b, где b = f ⁽ , , ) . a j =f-_ j sin (^ - j x ,.„ . ..

Здесь h j — длина элементарного отрезка с номером j .

После того как величины u i найдены, значения искомого фундаментального решения в узлах x i , т. е. ЧФР вычисляются с помощью формулы (1):

G (x)- g (xi)+ui.

Для дальнейшего удобно (но не обязательно), используя величины G (xi), получить интерполяционную формулу для фундаментального решения G (x). Теперь можно приступить к нахождению решения уравнения (5) с помо щью МТИ. Для этого справа и слева от области решения задачи, т. е. отрезка ю, в точках с координатами zl - -1 - 5x и zr - 1 + 5x размещаются заряды ql и qr, моделирующие искомое поле у(х) в области ю. Здесь 5x — удаленность за- рядов, моделирующих поле у(х), от границ области ю. Разумеется, должно выполняться условие l + 5x < d , т. е. точки zl и zr не должны выйти за пределы области Ω. Искомое решение представляем как суперпозицию полей двух то- чечных зарядов, т. е. в виде соотношения

у ( x ) = q l G ( l + x + 5 x ) + q r G ( l — x + 5 x ) .

Для окончательного решения задачи необходимо найти величины зарядов q_l и q_r , используя два каких-либо дополнительных условия, накладываемых на волновую функцию ψ( х ). Очевидно, что физический смысл имеют только четные и нечетные волновые функции. Отсюда следует, что заряды q l и q r либо равны друг другу ( q l = q r = q ), либо имеют противоположные знаки ( q l = — q r = q ). Величину заряда q следует выбрать так, чтобы удовлетворить условию нормировки волновой функции, например, потребовав, чтобы максимальное по абсолютной величине значение волновой функции в области решения ω равнялось единице.

Известно [22], что решение уравнения (6) имеет реальный физический смысл не при любых значениях энер-

Й ю        I 1 )

гии Е, т. е. параметра е, а только при E = "^е = Йю I n + — I, где квантовое число n может принимать только целочис- ленные значения, начиная с нуля. Только при этих значениях квантового числа волновая функция на бесконечности обращается в ноль. Очевидно, что при этом на границах области решения волновая функция будет иметь значения заметно меньшие, чем при других, не целочисленных значениях числа n.

Назовем величину K = 1/ ( |у( — l )| + |у( l )| ) критерием задачи. На рис. 1 представлен график зависимости кри

^

<и cd терия задачи K от энергии частицы, точнее, от числа n, которое изменяется в пределах от 0 до 10. Находились четные решения уравнения Шредингера. Вычисления проводились при числе узлов в области Ω N = 100.

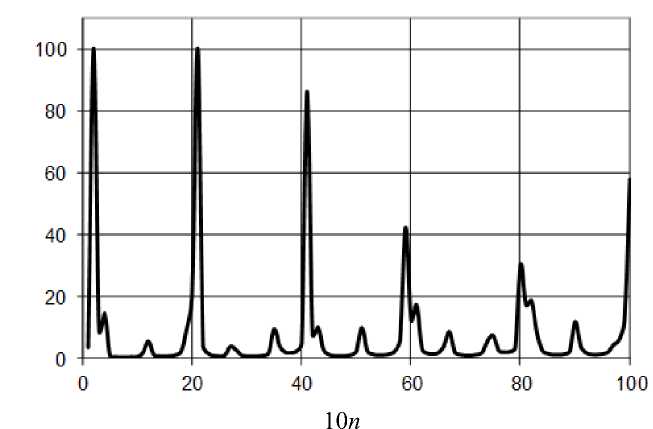
Рис. 1. Зависимость параметра K = 1/(|у ( — l )| + |у ( l )| )

от квантового числа n

Из рис. 1 видно, что максимумы на кривой соответствуют значениям квантового числа n , близким к 0, 2, 4, 6, 8 и 10. Это в точности согласуется с известными результатами квантовой теории для собственных значений энергии и для состояний осциллятора с четными волновыми функциями. Соответствующая зависимость K = K ( n ), полученная для нечетных волновых функций, имеет максимумы при нечетных целочисленных значениях квантового числа n .

Решение уравнения Шредингера (5) в аналитическом виде [22]:

I „2 I

I x I у n ( ^x ) = A exp I ^— у I H n ( ^x ) ,

где Hn (x) — полином Эрмита степени n, сравнивалось c волновой функцией у(х), рассчитанной по формуле (8), и погрешность численного метода оценивалась с помощью формулы е = maxlyn (x) — у(x)|.

x е ю

При вычислении погрешности е волновая функция (9) нормировалась так же, как и волновая функция ^( х ), т. е. нормировочный множитель А в (9) выбирался таким, чтобы максимальное по абсолютной величине значение волновой функции у n ( x ) в области решения ю равнялось единице. Очевидно, что точность численного решения зависит от числа узлов в области О, т. е. от числа N . На рис. 2 представлены такие зависимости, полученные при значениях кантового числа n = 0 (жирная сплошная линия); n = 2 (тонкая сплошная линия); n = 4 (пунктирная линия).

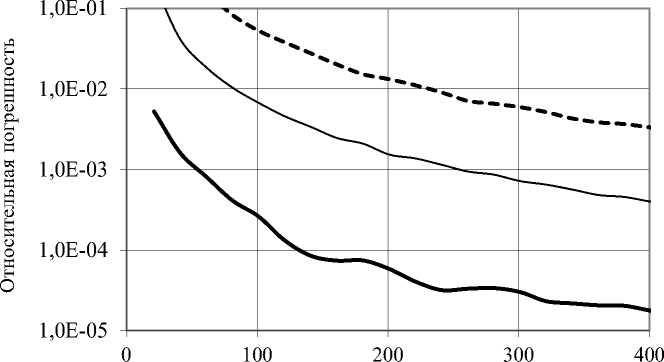
Количество узлов N

Рис. 2. Зависимость погрешности численного решения для волновой функции от числа узлов N в области решения для разных значений квантового числа n : n = 0 (жирная сплошная линия); n = 2 (тонкая сплошная линия); n = 4 (пунктирная линия)

Таким образом, применение численного фундаментального решения позволяет не только найти волновые функции, т. е. решить уравнение Шредингера, но и установить собственные значения энергии. Точность полученных результатов легко регулируется путем изменения числа узлов N в области решения задачи. Снизить погрешность решения можно также, используя более точный метод численного интегрирования.

Тестовый пример решения двумерной краевой задачи. В качестве второй тестовой задачи решалась задача Дирихле для уравнения Гельмгольца

А U + X U = 0

в круговой области ю радиусом r0. При использовании МТИ заряды, моделирующие искомое поле, располагались на вспомогательной окружности радиусом Rq = к• r0, где постоянная к > 1 определяет удаленность моделирующих зарядов от границ области ω. При решении данной тестовой задачи применялись ЧФР для уравнения Гельмгольца, вычис- ленные с использованием

в

фундаментальных решений для уравнения Лапласа g (r, R) = — ln|r - R\. Таким образом, 2п данной задаче L = А и l = X . В качестве области интегрирования Q в (4) использовался круг радиусом R0. На геометрические параметры задачи накладывалось условие r0 + Rq < R0. Моделировалось поле Гельмгольца точечного заряда, помещенного в точку р = (Xq,0) на оси X. Известные потенциалы этого поля сравнивались с вычисленными с помощью МТИ при использовании ЧФР значениями, и вычислялась относительная среднеквадратичная погрешность ε решения. При численном интегрировании в уравнении (4) использовались значения подинтегральных функций в узлах равномерной прямоугольной сетки. Количество узлов N сетки, находящихся внутри или на границе области Q, является одним из важнейших параметров задачи, определяющим точность ее решения. Часть этих узлов в количестве Nu находится внутри области решения задачи ю. Другим важным параметром является количество моделирующих зарядов Nq, равномерно располагаемых на вспомогательной окружности. На рис. 3 представлены зависимости среднеквадратичной погрешности е от количества узлов Nu в области ю. Вычисления производились при следующих значениях параметров: Nq = 50; r0 = 2; к = 1,3; Rq = k-r0; R0 = 5.

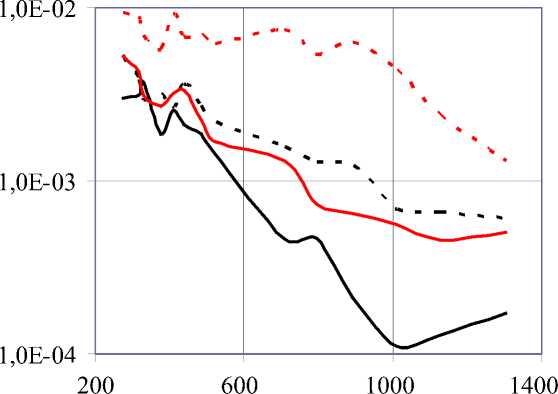
Количество узлов

Рис. 3. Зависимость среднеквадратичной погрешности ε от количества узлов N_u в области решения задачи ω для разных значений параметра λ: λ = –0,5 (черная пунктирная линия); λ = –1,0 (черная сплошная линия); λ = 0,5 (красная пунктирная линия); λ = 1,0 (красная сплошная линия)

Кривые, представленные на рис. 3 черным цветом, получены при отрицательных значениях параметра λ: пунктирной линии соответствует λ = –0,5; сплошной линии соответствует λ = –1,0. Кривые, представленные на рис. 3 красным цветом, получены при положительных значениях параметра λ: пунктирной линии соответствует λ = 0,5; сплошной линии соответствует λ = 1,0. Из данных рис. 3 видно, что при решении краевой задачи предложенным способом легко достигается решение с относительной среднеквадратичной погрешностью порядка 10 ^–4–10 ^–3. Этот результат можно считать вполне приемлемым. Кроме того, из рис. 3 видно, что, как и следовало ожидать, погрешность результата убывает с ростом количества узлов N_u в области ω. Можно ожидать, что при использовании более точного, по сравнению с методом прямоугольников, метода численного интегрирования в выражении (4) можно получить более точное численное решение краевой задачи и более быстрое снижение погрешности с ростом числа узлов N_u .

Выводы Рассмотренные выше тестовые примеры подтверждают возможность использования ЧФР при решении краевых задач с помощью МТИ. Особенно эффективно применение предложенного способа при решении задач Дирихле для уравнений со сферически симметричными фундаментальными решениями. Таким свойством обладают, например, фундаментальные решения для уравнений Лапласа и Гельмгольца. В этом случае фундаментальное решение зависит только от величины аргумента, т. е. от длины радиус-вектора r , а не от его ориентации. Поэтому в уравнении (4) можно предварительно произвести интегрирование по угловым координатам и получить одномерное интегральное уравнение для численного нахождения функции u ( r ) и вычисления ЧФР, которое в этом случае представляет собой одномерный массив чисел. Так как после нахождения ЧФР вычисление производных для фундаментальных решений легко производится с помощью соотношений подобных (5), то это делает возможным решение задач Неймана и краевых задач третьего рода. Следует отметить также, что ЧФР, полученные для некоторой области Ω, могут использоваться в МТИ при решении различных краевых задач для различных областей ю с Q .