Применение преобразователей электроэнергии с промежуточным резонансным звеном (колебательным контуром) становится все более востребованным, так как обеспечивает безопасное переключение транзисторов без дополнительных реактивных элементов и улучшает энергетические характеристики не только преобразователя, но и системы электропитания в целом. Также резонансный контур может применяться как преобразователь импеданса, в этом случае используются более сложные контуры, например, Т-образные. Применение таких контуров обеспечивает параметрическую стабилизацию как выходного тока при питании от источника напряжения [1–3], так и наоборот выходного напряжения при питании от источника тока, например, от солнечной батареи. В этом случае изменение нагрузки даже в широких пределах не приводит к существенным изменениям выходного параметра. Одним из вариантов реализации резонансного преобразователя тока солнечной батареи в стабильное напряжение питания является резонансный преобразователь с LCL-контуром, построенный по схеме двойного активного моста, к достоинствам которого следует отнести стабильность установившегося выходного напряжения и резонансной частоты при изменениях нагрузки [4]. Ток солнечной батареи не является постоянной величиной, его значение обусловлено несколькими факторами, в частности освещенностью и старением материалов, из-за чего в схему преобразователей энергии солнечной батареи приходится вводить отрицательную обратную связь (ООС) для стабилизации выходных параметров. Однако применение схем с параметрической стабилизацией позволяет существенно снизить глубину применяемой ООС, в результате чего существенно повышается энергетическая эффективность преобразователя, поскольку в качестве управляющего воздейст- вия в подобных схемах обычно применяется широтно-импульсная модуляция напряжения на выходе инвертора или входе выпрямителя [4; 5].

Ввиду наличия большого количества реактивных элементов для резонансных преобразователей характерна достаточно сложная динамика переходных процессов, что выражается в появлении затяжных выбросов выходного напряжения большой амплитуды и большого перерегулирования при смене нагрузки. В случае питания от источника тока выбросы напряжения могут присутствовать не только на выходе, но и на входе преобразователя, так как на динамические процессы начинает влиять входной фильтр. В настоящее время системы электропитания предъявляют весьма жесткие требования к качеству выходного напряжения, поэтому наличие сложной динамики переходных процессов ограничивает применение резонансных преобразователей. Одним из путей улучшения динамических свойств является введение ООС, которая необходима и для улучшения статических характеристик. Однако исследования показывают, что такая мера оказывается малоэффективной ввиду того, что диапазон регулирования ограничен, а время переходных процессов преобразователя при скачкообразном изменении нагрузки меньше аналогичного показателя при изменении управляющего воздействия. Таким образом, актуальной является задача улучшения динамических характеристик преобразователя без использования ООС.

В источниках, посвященных преобразователю с LCL-контуром, как правило, исследуется его работа в установившемся режиме и проводится анализ энергетических характеристик [2; 6–17]. Динамические свойства такого преобразователя исследовались мало, соответственно, нет достаточного количества информации о влиянии параметров элементов схемы на переходные процессы. Существует математическая модель, построенная на основе операторного метода [18], которая позволяет получить достаточно наглядное представление о работе преобразователя энергии солнечной батареи на основе LCL-контура, но подробный анализ динамических свойств на основе этой модели не проводился, он является одной из целей данной работы.

В большинстве работ, посвященных исследованию динамики резонансных преобразователей, рассматриваются преобразователи с последовательным резонансным контуром [19–23]. При этом из-за сложности резонансных преобразователей их динамические свойства часто исследуются компьютерным имитационным моделированием [24; 25] или методом переменных состояния, позволяющим получить векторно-матричные соотношения и проводить поинтервальный расчет переходных процессов [26–29], что опять же приводит к необходимости компьютерного моделирования. Данные методы достаточно точно моделируют переходные процессы при заданных значениях номиналов элементов схемы, однако не дают представления о том, как изменение параметров схем влияет на качество переходных процессов. Также для анализа резонансных преобразователей применяются частотный и операторный методы, основанные, соответственно, на преобразованиях Фурье и Лапласа [10–12, 14; 17; 30; 31]. При этом возможен анализ схем как по первой гармонике, так и с учетом синусоидальных составляющих более высокого порядка. Применительно к цепям с нелинейными элементами данные методы имеют не самую высокую точность, однако дают достаточно простое и понятное представление о работе схемы [19; 20]. При этом в независимости от разновидности колебательного контура приходится иметь дело с системой, имеющей порядок более двух, поскольку в схемах преобразователей присутствуют входные и выходные фильтры.

В данной статье на основе подходов, основанных на анализе по первой гармонике, рассмотрено улучшение качества переходных процессов в LCL-преобразователе энергии солнечной батареи путем применения дополнительного низкочастотного фильтра в выходной цепи, а также показана эффективность применения операторного метода для анализа модернизированной схемы.

Преобразователь энергии солнечной батареи на основе LCL-контура и его динамическая модель

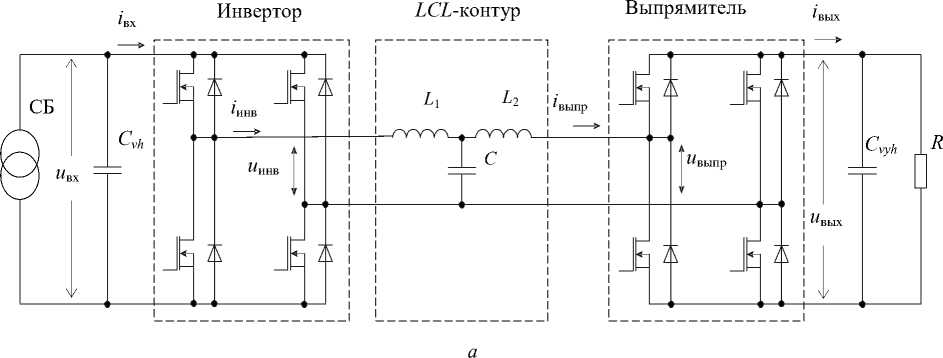
Анализируемый резонансный преобразователь содержит два мостовых преобразователя (инвертор и выпрямитель), связанных колебательным LCL-контуром, к выходу схемы подключены нагрузка и выходной сглаживающий фильтр (рис. 1). Инвертор формирует прямоугольное на- пряжение Uинв, подаваемое на вход LCL-контура. При условии совпадения частоты преобразования инвертора с резонансной частотой контура в индуктивности L1 возникает синусоидальный ток Iинв, совпадающий по фазе с Uинв. При этом в индуктивности L2 возникает ток Iвыпр, сдвинутый относительно Iинв на угол π/2, не зависящий от нагрузки. Поэтому сигналы управления выпрямителя сдвинуты относительно сигналов управления инвертора на аналогичный угол π/2, при этом напряжение выпрямителя Uвыпр совпадает по фазе с током. При условии равенства индуктивностей L1=L2 обеспечивается стабильность выходного напряжения при изменении нагрузки и стабильность угла сдвига между токами дросселей L1 и L2, равного π/2 [4]. Если при этом сопротивление нагрузки превышает единицы Ом, то резонансная частота, волновое сопротивление контура, добротность и выходное напряжение определяются формулами:

Q = 8 R- , πρ

^2

U вых = _o^P I СБ , 8

где I _СБ – входной ток преобразователя.

б

Рис. 1. Схема резонансного преобразователя энергии солнечной батареи с LCL-контуром ( а ) и диаграммы его параметров ( б )

Fig. 1. Diagram of a resonant solar battery energy converter with an LCL circuit ( a ) and diagrams of its parameters ( б )

Согласно формулам (1), напряжение на выходе преобразователя определяется только значениями питающего тока и волнового сопротивления колебательного контура и никак не зависит от сопротивления нагрузки. При работе рассматриваемого преобразователя с солнечной батареей, работающей на токовой ветви, сопротивление нагрузки преобразователя тоже влияет на значение выходного напряжения, поскольку при движении рабочей точки в пределах токовой ветви ток немного падает с ростом напряжения на солнечной батарее. Однако это падение является незначительным, поэтому в дальнейших рассуждениях солнечная батарея заменяется идеальным источником тока.

В установившемся режиме выходное напряжение не зависит от сопротивления нагрузки, но скачкообразное изменение последнего приводит к появлению динамических выбросов, определяемых параметрами схемы. В [18] была разработана математическая модель, позволяющая дать качественные и количественные оценки динамики рассматриваемой схемы и связать их с параметрами схемы при равенстве частоты преобразования и собственной частоты LCL-контура.

Согласно этой модели, преобразователь можно представить в виде эквивалентного низкочастотного колебательного контура (рис. 2), параметры которого определяются формулами:

( 2²n ^ ² vl ’ Cvyh • ^R Э =

^- p I ¹

_V 8 J R ^,

V 8 J

®0Э = 1 4 L Э C vh - 2 77--77“ ^{— P}\ C vh ’ C vyh

\ L _э     ^{— p C}vyh

^Рэ~ IQ" 8 K T’

^Q Э ^{- р} э / ^R Э ^-

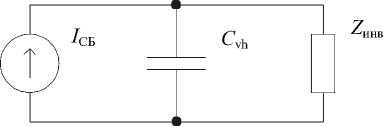
Рис. 2. Эквивалентная схема преобразователя с LCL-контуром при питании от источника тока

Fig. 2. Equivalent circuit of a converter with an LCL circuit when powered by a current source

8 R   ^Сvyh

π ² ρ   С vh

u L +(+H вых+

Q

1+ =

1 + 2 5 R • e ^{2 Q э+} Sh ^{Q 1 + +} V1 - 4 Q 2+

1 + 25R -т0Э +e ““0Э+

при Qэ+ < 2, при QЭ+ = 2,

_^оэ£ .,

Sin ^2++1

1 + 2 5 R • e ^{У Э+        2 +}    при Q э+ > -,

V 4 QЭ+ -1

71 -4 Q o

2 Q Э+

^Ю 0Э ’

= J 4 Q Э+ - 1 2 Q Э+

^Ю 0Э ’

где 5 R = ( R ₊- R _-)/ R _- - относительное изменение нагрузки; R _-, R ₊ - сопротивления нагрузки до и после её изменения, соответственно; Q _Э–, Q _Э+ – добротности эквивалентного колебательного контура до и после изменения нагрузки, соответственно.

Данная модель показывает, что единственным способом улучшения качества переходных процессов в данной схеме является увеличение емкости выходного фильтра, но эффективность данной меры подробно не рассматривалась.

Как известно, качество переходного процесса оценивается величиной максимального отклонения от номинального значения и временем переходного процесса. Относительное значение максимального отклонения от номинала можно найти путём решения задачи поиска экстремума функции, являющейся переменной частью выражений (3):

5 U max

( 1

^Cvh • e

I Q -   Q + Л c _Vy_h

arctgJ ⁴ Q + c vyh ^-i

Сvh

-

J 4 Q + C -1 ^С vh

,

где Q _Э–, Q _Э+ – добротности LCL-контура до и после изменения нагрузки, соответственно.

При достаточно больших C vyh , зависимость (4) становится близка к обратно пропорциональной квадратному корню из C vyh , следовательно, с увеличением выходной емкости эффективность улучшения качества переходного процесса снижается. Кроме того, из (2) и (3) видно, что время переходного процесса увеличивается пропорционально C vyh .

При расчете преобразователя на выходное напряжение 100 В при входном токе 8 А и при частоте преобразования 100 кГц для обеспечения условия 5 U _max< 10 % значение C_vyh составляет сотни мкФ, а время переходного процесса превышает сотни мс.

К напряжению питания бортовой космической аппаратуры из соображений электромагнитной совместимости предъявляются достаточно жесткие требования к форме переходных процессов, например, 5 U вых < 1 % в течение первых 5 мс и еще меньше в течение последующего времени. В этом случае потребуется значение С_vyh величиной в десятки мФ. Конденсаторы такой емкости, рассчитанные на напряжения в десятки вольт при работе на частоте преобразования в десятки кГц, по своим габаритам и массе в несколько раз превосходят аналогичные показатели остальной части преобразователя. К тому же, при этом приходится сильно замедлять выход преобразователя на полную мощность на старте – до нескольких секунд. Таким образом, увеличение значения С vyh является малоэффективной мерой для улучшения качества переходных процессов преобразователя при ступенчатом изменении нагрузки.

Дополнительный низкочастотный выходного RC-фильтр для улучшения качества переходных процессов резонансного LCL-преобразователя

Анализ математической модели, представленной выражениями (3)–(5), подсказывает один из путей улучшения качества переходных процессов резонансного LCL-преобразователя –

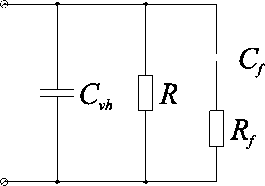
Рис. 3. Выходная цепь резонансного LCL-преобразователя при подключении низкочастотного RC-фильтра

фильтрация низкочастотных колебаний переходного процесса при помощи RC-цепи на выходе схемы, подключенной параллельно высокочастотному фильтру, как показано на рис. 3, где R f и C f – соответственно, сопротивление и емкость низкочастотного фильтра. Компьютерное моделирование показывает высокую эффективность данного решения, особенно для снижения времени переходных процессов. Но при этом оно занимает значительное время и не дает ответ на вопросы, как зависят параметры переходных процессов от величин элементов дополнительного RC-фильтра и при каких значениях этих величин эффективность улучшения качества переходных процессов будет максимальной. Для ответа на эти вопросы необходим анализ предложенного способа, в рамках которого следует получить линеаризованную эквивалентную схему преобразователя, позволяющую перейти от компьютерного моделирования к аналитическим выражениям.

Fig. 3. Output circuit of a resonant LCL converter when connecting a low-frequency RC filter

Цепь на рис. 3 имеет второй порядок, является апериодической и её можно охарактеризовать следующими параметрами:

Q ф =

^т ф = ^Rf^Cf ,

“ ^ф = f RC

.

RC vyh ₊

R f C f

fL ₊

RCvyh

RC _f

R f Cvyh

Достаточно легко доказать, что параметр Q ф не может превышать значения 0,5.

Операторное сопротивление рассматриваемой цепи можно получить из её схемы. После приведения к определениям (5) оно имеет следующий вид:

Z ф ( p ) =

R «ф ( 1 + p Тф )

«ф

«ф+ p   + p

Q _ф

Выражение для переходного процесса напряжения при воздействии ступенчатого изменения тока I ф несложно получить из (6) операторным методом:

u ф ( t ) = I ф R Ь— 2

(

1 +

к

¹ — ² « ф Т ф О ф

. i—4 Q2 ^

—

« ф t

_e 2 Q ф

+

1 _— ^{1 — 2} « ф ^Т ф О ф

к

—

« ф t

_e 2 Q ф

7

Пример графика переходного процесса приведен на рис. 4. Характерной особенностью переходного процесса является быстрое экспоненциальное нарастание вначале с последующим существенным замедлением. Такую же форму имеет выходное напряжение выпрямителя при исключении пульсаций высокочастотного преобразования.

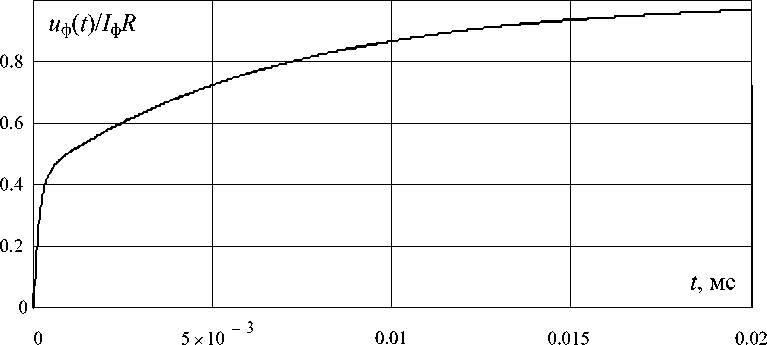
Рис. 4. Переходный процесс в выходной цепи преобразователя при воздействии единичного скачка тока при R = 12 Ом, R f = 10 Ом, С_vyh = 30 мкФ, С f = 300 мкФ

Fig. 4. The transient process in the output circuit of the converter under the influence of a single current surge at R = 12 ohms, R f = 10 ohms, С_vyh = 30 mkF, С f = 300 mkF

Построение операторной модели выпрямителя

В результате воздействия на вход выпрямителя скачка синусоидального тока c единичной амплитудой и частотой преобразования, на этом же входе возникает прямоугольное напряжение, совпадающее по фазе с током, с огибающей, повторяющей форму напряжения на выходе выпрямителя, определяемого выражением (7). При замене прямоугольника его первой гармоникой напряжение на входе выпрямителя определяется выражением:

uвх= (t) = — c(t)sin(®0t)uф (t), П где c(t) - функция Хевисайда; ю0 - частота преобразования.

Для анализа динамических свойств необходимо произвести преобразование Лапласа от тока и напряжения на входе выпрямителя, для чего удобно воспользоваться теоремой об умножении оригинала на гармонику:

и ф ( х ) sin ® ₀ t = и ф ( x ) cos I ® ₀ t -

П15 U (p ) =2

- j n                  j n e 2UUф (p - J®0) + e 2иф (p + J®0) •

С учётом выражений (6) и (9), току и напряжению на входе выпрямителя в операторном виде соответствуют следующие выражения:

iвх = (t) = ° (t)sin(®0t) 5 IBX = (p) =  2 ®0 2

P +® 0

_______®0_______

( p ^- j ^Ш о )( p + j ® 0 ) ’

u вх= ( t ) ⁵ U BX = ( p ) = — n ²

-4 RJ ®ф [1 + (p - j ®0 )т

+

® ф ⁺( p ^- j ® о ) ® ф ⁺ ( p ^- j ® 0 ) ² ( p ^- j ® 0 )

Qф

+4 Rj ®ф [1 + (p + j ®0 )t

п2 ®ф +(p + j®о )®ф + (p + j®0 )2 _              Qф

( p ⁺ j ® 0 )

Из формул (10) следуют выражения входного сопротивления выпрямителя в операторном и частотном видах:

7  ( _}  4 R « Ф

Z вх = ( P ) =^

^П « 0

- j [1 + ( P - j «0 К ]( P + J «0 ) + j [1 + ( P + J «0 К ]( P - J «0 ) > «Ф +( P - j «0 )«ф + ( P - j «0 )2 «ф +( P + j «0 )«ф + ( P + j «0 )2

У ф                    Q

После приведения к общему знаменателю видно, что операторное сопротивление выпрямителя, нагруженного на рассматриваемый выходной фильтр, имеет четвёртый порядок. Графики модуля сопротивления в частотном виде говорят о его резонансном характере (рис. 5).

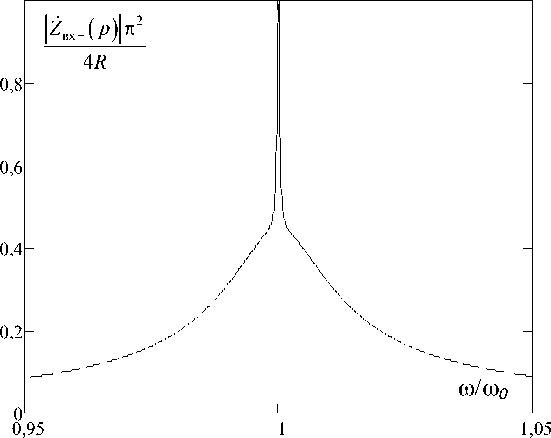
Рис. 5. Модуль частотного сопротивления выпрямителя при R = 12 Ом, R f = 10 Ом, С vyh = 30 мкФ, С f = 300 мкФ

• Fig. 5.    The frequency resistance module of the rectifier at R = 12 ohms, R f = 10 ohms, С vyh = 30 mkF, С f = 300 mkF

Анализ динамических свойств преобразователя при питании от источника постоянного напряжения

Проанализировать динамику LCL-контура можно путем определения его реакции на скачок синусоидального напряжения. В качестве откликов следует рассмотреть входной ток и напряжение на нагрузке. Передаточные функции несложно определить из его эквивалентной схемы, изображенной на рис. 6. Динамические свойства преобразователя легко следуют из динамики LCL-контура путем исключения колебаний на частоте преобразования.

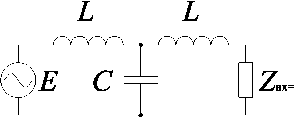
Рис. 6. Эквивалентная схема LCL-контура, нагруженного на выпрямитель, при питании от источника напряжения

• Fig. 6.    Equivalent circuit of an LCL circuit loaded on a rectifier when powered by a voltage source

  Передаточные функции легко можно выразить через операторное сопротивление контура:

  
  

  Z () - L ₊     PL + Z вх • ( P )     - PL ( ² + P^{2 LC} ) + ^Z вх- ( P ) ( P ^{2 LC} + 1 )

  к ^{P P}   1 + [ PL + Z _BX - ( P ) ] PC        1 + P ² LC + pCZ _bx - ( P )

  
  
  
  

  Передаточной функцией для нахождения входного тока контура является его входная проводимость:

  
  

  G к ( P ) ^-

  
  

  1 =       1 + P ² LC + pCZ bx - ( P )

  ^Z K ⁽ P ) pL ( 2 + P²LC ) + Z bx - ( P ) ( P²LC + 1 ) .

  
  
  
  

  Передаточная функция по напряжению:

  
  

  K ( _P ) = ^Z к ⁽ P ^{) -} PL . ^Z bx - ⁽ P ) =_____________ ^Z bx - ⁽ P ) _____________

  ^{1       Z} K ( P )     ^Z bx - ( P ) ⁺ PL PL ( 2 + P ² LC ) + Z _bx = ( P ) ( P ² LC + 1 ) ■

  
  

  Изображения входного тока контура и напряжения на входе выпрямителя при подаче скачка синусоиды в операторном виде определяются следующими выражениями:

  
  

  1 ^{1 (} s ) 7 ( V 2 iV

  ^Z к ( P ) ( P ⁺ 1 )

  , X K ( P )

  U выпр ⁽ P ^{) -} 2    .

  P + 1

  
  
  
  

  С учетом выражения (11) следует, что полученные передаточные функции имеет шестой порядок, что значительно затрудняет поиск отклика контура. Ввиду высокого порядка получившихся выражений и резонансного характера рассматриваемой системы, а также из-за того, что в конечном итоге требуется исследовать динамические напряжений и токов на входе и выходе преобразователя, для поиска откликов целесообразно воспользоваться методом низкочастотного эквивалента, который применяется для анализа сложных колебательных систем. При этом вместо передаточных функций всей колебательной системы рассматриваются передаточные функции для комплексных огибающих сигналов на входе и выходе, что позволяет снизить порядок выражений для описания системы.

  После необходимых преобразований получено следующее выражение передаточной функции для комплексной огибающей напряжения в операторной форме:

  
  

  K НЧ ^{( P} ) ^-

  
  

  ^{- jQ} юф ( 1 ⁺ P ^т ф )

  2 ,    ®ф , 2

  ®ф ⁺ Pn ⁺ P Q _ф

  
  
  
  

  Для получения комплексной огибающей напряжения на входе выпрямителя при воздействии синуса на вход контура нужно взять обратное преобразование Лапласа от произведения (16) на j / p. Напряжение на выходе выпрямителя отличается от комплексной огибающей напряжения на его входе только множителем п /4, поэтому после всех необходимых преобразований оно определяется следующим выражением:

  
  
  
  

  и^ х( t ) -- Q | 1

  вых ₄

  
  
  
  

  1 +

  
  

  ¹ " ² ® ф ^т ф 0 ф

  
  
  
  
  
  

  --1

  
  

  e

  
  

  +

  
  
  
  

  _

  
  

  ^{1  2 ю} ф ^т ф^

  
  
  
  

  --1

  
  

  e

  
  

  .

  
  
  
  

  \

  
  

  7

  
  

  \

  
  

  7

  
  

  Передаточная функции для комплексной огибающей тока контура в операторной форме:

  
  

  G H4 ( p ) =

  
  

  j Q юф ( 1 + p Тф )

  
  

  ^p 2 ,    ®ф , 2

  ®Ф + Рп + P Q _ф

  
  
  
  

  Полученное выражение отличается от (16) только множителем 1/ р , а модуль комплексной огибающей тока контура отличается от тока инвертора множителем 2/ п , поэтому в итоге, после соответствующих выкладок, получается следующее выражение для тока инвертора:

  
  

  i ... ( t ) = ² Q п р

  
  

  1 -

  
  
  
  

  1 +

  
  

  1 - 2щлЯ

  V1 - 4 е ф ,

  
  

  ®ф£ (

  2 е ф I

  
  

  1- д-4 е 2 ф

  
  

  +

  
  

  \

  
  

  1 - 2щл е ф ] 1 - ⁴ е ф ,

  
  

  ^щ ф t (

  2 е ф I

  
  

  1+, 1-4 е ² ф

  
  
  
  

Зависящие от времени части выражений (17) и (19) содержат параметры выходного фильтра, а параметры контура выступают только в качестве коэффициента пропорциональности, из чего следует, что инерционные свойства входа и выхода преобразователя не зависят от параметров колебательного контура и определяются только элементами выходного фильтра, что объясняется тем, что постоянная времени фильтра намного больше постоянной времени нарастания тока контура.

Синтез эквивалентной схемы преобразователя

Сопоставление выражений (17) и (19) показывает, что ток инвертора и напряжение на выходе выпрямителя связаны простым выражением, совпадающим по форме со статической функцией передачи преобразователя:

« вы х( t ) =—^Р ' ин в( t ) •                                       (20)

вых        8 инв

Полученное выражение говорит о том, что инвертор можно представить в виде цепи, качественно являющейся дуальной цепью по отношению к выходной цепи. В [18] при анализе преобразователя без фильтра был получен именно такой результат. Инвертор был представлен в виде цепи, представляющей собой последовательное соединение сопротивления и емкости, что качественно является дуальной цепью по отношению к выходному фильтру, представляющему собой параллельное соединение сопротивления нагрузки и емкости подавления высокочастотных пульсаций. При наличии в составе выходной цепи низкочастотного фильтра эквивалентная схема инвертора должна представлять собой последовательное сопротивление эквивалентных элементов L Э и R Э , найденных ранее, с параллельным соединением элементов L ФЭ и R ФЭ , как показано на рис. 7.

В этом случае операторное сопротивление можно представить следующим выражением:

Z инв ( Р ) = R Э

L Э + L ФЭ ₊ ^L ФЭ ] „ ₊ L Э ^L ФЭ „2 I ^{Р Р} <  R Э ^R ФЭ R Э J    R Э R ФЭ

1 + ^{/ :} Э р ^R ФЭ

С другой стороны, входное операторное сопротивление инвертора можно найти из изображения тока инвертора, являющегося откликом на единичный скачок напряжения, которое следует из (18) с учетом выпрямления и замены прямоугольного напряжения на выходе инвертора его первой гармоникой, и с учетом (5) определяется выражением:

Z инв ( P ) =

Пр 1 + P ( R yh C yh + R f C f + R vyh C f ) + R vyh C yh R f C fP²

8 Q                 1 + pR f C f

Если сопоставить выражения (21) и (22), то можно получить выражения для элементов эквивалентной схемы инвертора:

r, -^

^Э 8 Q 1

\ ° 7

R ’

L _Э

_D    Rvyh C vyh

R _Э

^ LЭ =

п2р

< 8 7

> 2

C yh .

^L ФЭ

_D ^- R vyh C f ^ L ФЭ ^- R _Э

ФЭ - R f C f ^ ^R ФЭ - ^R ФЭ

\    7

\ ° 7

C f ,

R f

.

Следует заметить, что значения L Э и R Э получись такими же, как и в случае анализа преобразователя без дополнительного низкочастотного фильтра, что подтверждает правильность эквивалентной схемы инвертора.

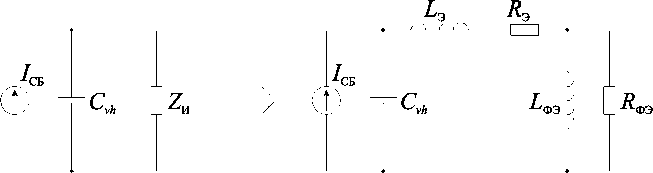
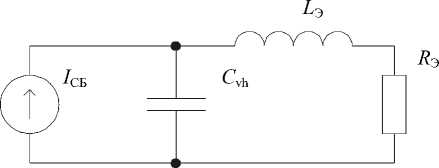
Рис. 7. Эквивалентная схема преобразователя с LCL-контуром при питании от источника тока

• Fig. 7.    Equivalent circuit of a converter with an LCL circuit when powered by a current source

Проверка полученных результатов путем компьютерного моделирования

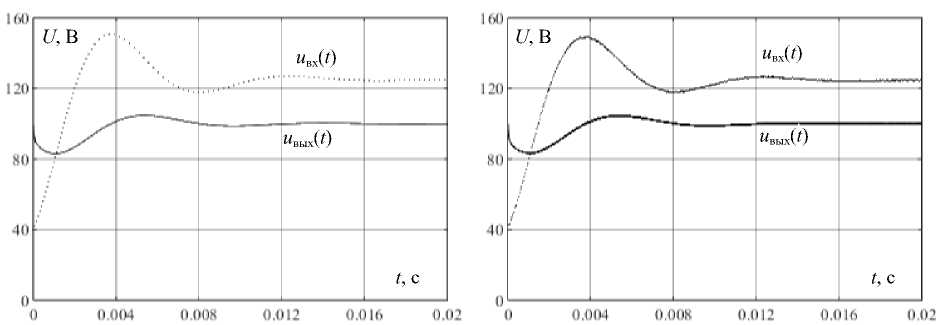
Для проверки полученных результатов в программной среде моделирования Matlab Simulink 2022b построена модель, содержащая исходную схему преобразователя и его эквивалентную схему. Примеры переходных процессов напряжений на входах и выходах преобразователя и его эквивалентной схемы при смене сопротивления нагрузки с 30 до 10 Ом и наоборот, показанные на рис. 8 и 9, соответственно, приведены при следующих значениях элементов схемы преобразователя: входной ток СБ I = 8 А, частота преобразования f = 100 кГц, номинальное выходное напряжение U вых = 100 В, емкость входного фильтра C vyh = 30 пФ, емкость высокочастотного выходного фильтра C vyh = 30 пФ, емкость низкочастотного выходного фильтра C f = 270 пФ, сопротивление низкочастотного фильтра R ф = 2 Ом. Необходимо отметить высокую степень совпадения, что говорит о справедливости вывода о незначительном влиянии колебательного контура на динамику преобразователя.

Полученная эквивалентная схема позволяет провести анализ переходных процессов, происходящих в преобразователе, путем решения соответствующих дифференциальных уравнений. Решение данных уравнений затруднено 3-м порядком системы и громоздкостью выражений. На момент написания статьи решения в виде относительно простых выражений, наглядно отражающих свойства эквивалентной схемы, получены не были. Однако с помощью эквивалентной схемы удалось значительно упростить и ускорить компьютерное моделирование переходных процессов преобразователя без учета высокочастотных пульсаций выходного напряжения. Время построения переходных процессов для исходной схемы составляет несколько минут, для эквивалентной схемы – несколько секунд, т. е. скорость моделирования увеличилась примерно в 60 раз.

б

Рис. 8. Переходные процессы при изменении сопротивления нагрузки преобразователя с 30 до 10 Ом: а – для эквивалентной схемы преобразователя; б – для преобразователя

Fig. 8. Transients when the load resistance of the converter changes from 30 to 10 ohms: a – for the equivalent converter circuit; б – for the converter

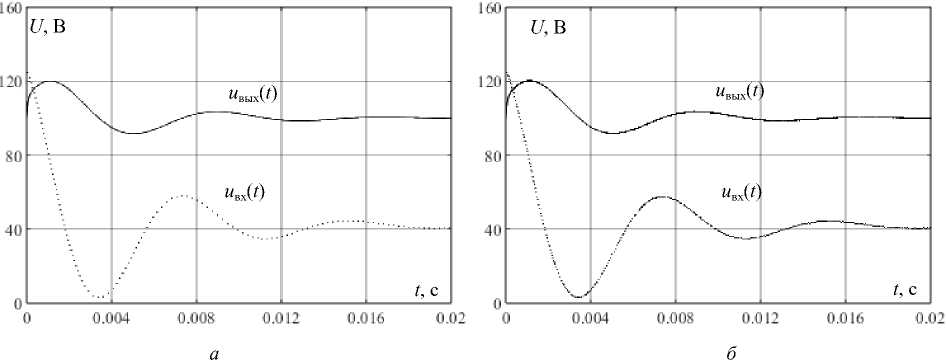
Рис. 9. Переходные процессы при изменении сопротивления нагрузки преобразователя с 10 до 30 Ом: а – для эквивалентной схемы преобразователя; б – для преобразователя

Fig. 9. Transients when the load resistance of the converter changes from 10 to 30 ohms: a – for the equivalent converter circuit; б – for the converter

Для сравнения эффекта от применения высокочастотного и низкочастотного фильтров были сняты характеристики при изменении сопротивления нагрузки с 10 до 30 Ом для следующих значений элементов схемы преобразователя: входной ток СБ I = 8 А, номинальное выходное напряжение U _вых = 100 В, емкость входного фильтра C_vh = 30 мкФ, емкость высокочастотного выходного фильтра C_vyh = 30 мкФ, емкость низкочастотного выходного фильтра C f = 270 мкФ. Сравнение производилось при одном значении емкости низкочастотного фильтра и нулевом и ненулевом значениях R f . При R f = 0 преобразователь соответствует схеме на рис. 1 с суммарной емкостью выходного фильтра равного сумме C_vyh и C f , т. е. 300 мкФ. Результаты показаны на рис. 10. Видно, что наличие ненулевого R ф существенно снижает время переходных процессов.

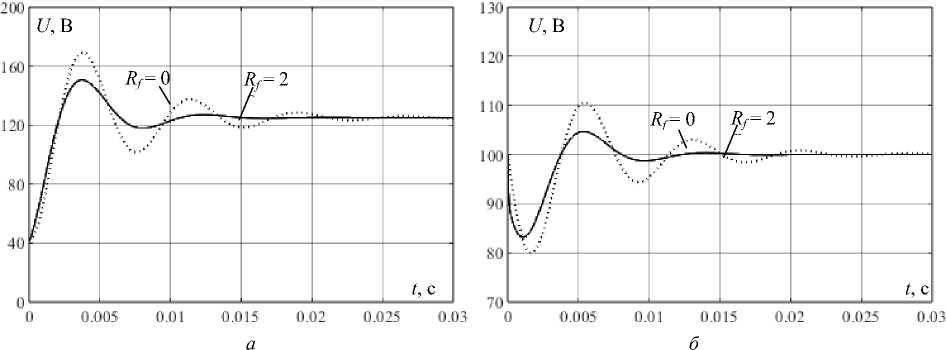
Рис. 10. Переходные процессы при изменении сопротивления нагрузки преобразователя с 10 до 30 Ом и разных значениях R f : а – для входного напряжения; б – для выходного напряжения

Fig. 10. Transients when the load resistance of the converter changes from 10 to 30 ohms and different values of R f : a – for the input voltage; б – for the output voltage

В ходе моделирования были так же замечены следующие закономерности:

• 1.    Амплитуда перерегулирования входного напряжения снижается с увеличением значений C f и R f . Но при этом с ростом C f увеличивается время переходных процессов, в то время как увеличение значения R f влияет на них противоположным образом.

• 2.    Для достижения максимального эффекта значения емкостей высокочастотных конденсаторов должны быть минимальными, определяемыми только требуемым уровнем высокочастотных пульсаций.

• 3.    Существует значение R f , при котором величина скачка выходного напряжения при смене нагрузки минимальна, но при этом она меньше аналогичного показателя при R f = 0 не более чем на 20 %.

Таким образом, амплитуда скачка выходного напряжения при смене нагрузки по-прежнему определяется емкостью выходного фильтра. Однако следует отметить, что последовательное соединение сопротивления и емкости является одним из вариантов эквивалентной схемы низкочастотного конденсатора, который по сравнению с высокочастотным при прочих равных условиях имеет гораздо меньшие массогабаритные показатели.

Заключение

• 1.    Несмотря на нелинейность резонансного преобразователя, обусловленную наличием ключевых элементов, его динамические свойства можно описать с помощью линейной математической модели. Вследствие того, что время переходных процессов у выходного фильтра как минимум на порядок больше, чем у колебательного контура, можно считать, что динамические свойства преобразователя определяются только его фильтрующими цепями на входе и выходе.

• 2.    Установлено, что, с точки зрения динамики входных и выходных параметров, резонансный LCL-преобразователь при питании постоянным напряжением можно заменить эквивалентной цепью, являющейся дуальной по отношению к выходному фильтру. При питании преобразователя от источника постоянного тока в эквивалентную схему добавляется входной емкостной фильтр и преобразователь можно рассматривать как эквивалентный колебательный контур. Похожий результат был получен в [18]. Путем замены преобразователя эквивалентным колебательным контуром получена математическая модель, не учитывающая высокочастотных пульсаций, при помощи которой удалось в несколько десятков раз увеличить скорость компьютерного моделирования и исследовать переходные процессы входного и выходного напряжений.

• 3.    Установлено, что применение дополнительного низкочастотного выходного фильтра при скачкообразном изменении нагрузки значительно сокращает время переходных процессов входного и выходного напряжений, значительно снижает амплитуду переходного процесса входного напряжения, а также способствует улучшению массогабаритных показателей преобразователя.