Применение фильтра Калмана к задачам управления причаливанием космических аппаратов

ШАНГАРЕЕВ А.Т.

ТИМАКОВ С.Н.

ПЛАТОНОВ В.Н.

Основные принципы построения бортовых динамических моделей

Появление бортовых цифровых вычислительных машин (БЦВМ) около 40 лет назад положило начало новому этапу в развитии систем управления движением и навигацией. Возникло новое направление науки и техники — создание бесплатформенных инерциальных навигационных систем (БИНС). В свою очередь, развитие БИНС открывает новые возможности для решения навигационных задач космических аппаратов. Этапы развития БИНС, связанные с переходом на высокопроизводительные комплексы БЦВМ, описаны в работе [1].

В настоящее время также продолжаются работы по модернизации алгоритмов БИНС, исходя из требований по улучшению качества выполнения встречи на орбите: сокращение продолжительности полета от времени старта до механического контакта космических аппаратов, уменьшение потребных затрат топлива и повышение точности причаливания. Навигационный контур, входящий в состав БИНС, представляет собой не что иное, как бортовую модель движения космического аппарата в заданном режиме полета. Во время полета данная модель корректируется по информации навигационных параметров от инерциальных датчиков и датчиков внешней информации, выполняя, по сути, роль динамического фильтра. Как правило, динамический фильтр реализован по классической схеме «корректор – предиктор», когда прогнозируемая на текущий момент времени информация о движении корректируется в бортовой модели БИНС [2].

В настоящей публикации рассматривается применение фильтра Калмана, реализованного в составе бортовой модели движения, для причаливания космического аппарата с упругими элементами конструкции. Процесс сближения космического аппарата с орбитальной станцией выглядит следующим образом:

• •    дальнее автономное сближение;

• •    облет космическим аппаратом орбитальной станции;

• •    зависание;

• •    причаливание и стыковка.

Согласно принятой в настоящее время схеме сближения, режим причаливания или, в более общем случае, режим облета (в зависимости от положения выбранного стыковочного узла станции относительно причаливающего аппарата) начинается с дальности 400 м между стыкующимися объектами. Орбитальная станция (далее — станция) в процессе сближения постоянно находится в орбитальной либо инерциальной ориентации, а причаливающий к станции космический аппарат (далее — корабль) совершает траекторные и угловые маневры в соответствии с законами управления. Настоящая работа актуальна для причаливания и стыковки многофункционального лабораторного модуля (МЛМ) как упругого корабля к Международной космической станции.

Вследствие выноса антенн аппаратуры «Курс» переменные, описывающие относительное движение стыкуемых объектов, искажены параллаксами и шумами переот-ражений радиосигналов от элементов конструкции станции. Параллаксационным искажениям подвержены также осциллирующие составляющие в сигналах с датчиковой аппаратуры, обусловленные упругими колебаниями конструкции взаимно причаливающих объектов. При формировании командных сигналов на управляющие органы по «сырым» измерениям с датчиков первичной информации указанные обстоятельства приводят к излишнему расходу рабочего тела и повышенным нагрузкам на конструкцию корабля.

С целью минимизации влияния вышеперечисленных помех на динамику корабля в режиме причаливания в контур управления вводится настраиваемая бортовая модель динамического поведения объекта управления, функционирующая в реальном масштабе времени и предназначенная для фильтрации этих помех в сигналах с датчиков первичной информации.

Общая постановка задачи

Корабль как объект управления на каждом такте n бортового компьютера (такт — интервал времени между двумя последовательными опросами бортовым компьютером датчиковой аппаратуры) характеризуется семью модами движения: тремя модами продольного и поперечного движений центра масс, тремя модами углового движения вокруг центра масс и одной модой упругих колебаний корабля вокруг продольной оси:

X = n

_X прод-попер

_X вращ колеб

X

На околоземной орбите вышеописанное движение складывается из невозмущенного X _n ^{н е} ₊ ^в ₁ ^озмущ = A X _n движения в гравитационном поле Земли и управляемого X _n ^уп ₊ ^р ₁ = B U _n движения. Эти дискретно-переходные процессы в пространстве состояний имеют следующий вид:

Xn + 1 = AXn + BUn + ν1n, где Xn — вектор состояния объекта управления; Un — вектор управления; A, B — матрицы переходных процессов и управления, соот- ветственно; ν1n — погрешность модели.

Ввиду независимости вышеописанных мод движения, их переходные процессы также будут взаимно независимы, и матрица переходных процессов будет иметь следующий блочно-диагональный (квази-диагональный) вид:

/ L 0 0\

A = I 0 R 0 , \ 0 0 H где подматрицы L, R, H находятся аналитически из уравнений движения корабля.

В измерительных каналах датчиковой аппаратуры «Курс» формируются сигналы относительной дальности ρ и скорости сближения ρ, а также углы ε _y , ε _z и угловые скорости пеленга ε _y , ε _z . В измерительных каналах волоконно-оптического трехосного измерителя угловой скорости (ТИУС) — угловые скорости γ, ψ, θ корабля вокруг своего центра масс.

Продольно-поперечное относительное движение корабля

Относительное продольно-поперечное движение корабля есть поступательное движение его центра масс относительно центра масс орбитальной станции в гравитационном поле Земли.

Введем орбитальные системы координат (ОСК) с началом О _А в центре масс корабля и с началом О _П в центре масс станции (рис. 1). Ось О _А Х ( О _П X ) направим вдоль орбитального движения корабля (станции), ось О _А Y ( О _П Y ) — вдоль радиус-вектора из центра Земли к центру масс корабля (станции), ось О _А Z ( О _П Z ) дополняет систему координат до правой тройки. Заметим, что в общем случае следует различать ОСК корабля и ОСК станции; однако при рассмотрении процесса причаливания допускается, что направления соответствующих осей ОСК станции и корабля близки друг к другу, так как априори корабль выводится на орбиту станции.

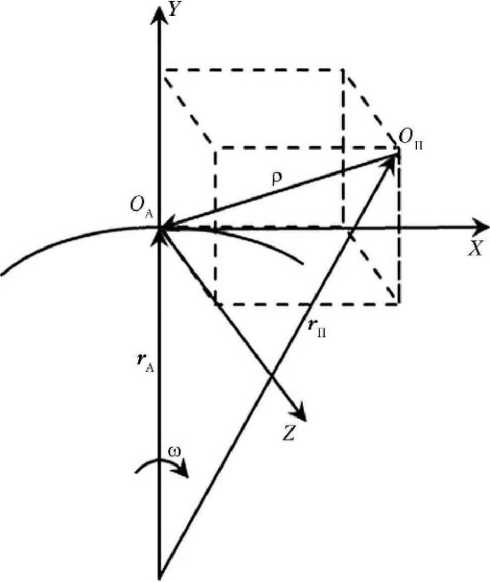
о

Рис. 1. Продольно-поперечное относительное движение центров масс причаливающих объектов в орбитальной системе координат корабля: О — центр Земли; О_А, О_П — центры масс корабля и станции, соответственно; r А , r _П — радиус-векторы из центра Земли к центрам масс корабля и станции, соответственно; ρ — относительная удаленность центров масс взаимно-причаливающих объектов; ω — орбитальная угловая скорость корабля

Так как параметры орбиты станции хорошо известны, достаточно просто выписываются уравнения движения корабля и станции в инерциальной системе координат, а после некоторого количества преобразований — линеаризованная система уравнений движения корабля относительно станции в ОСК корабля. Это уравнения Hill [3] с дополнениями Clohessy–Wiltshire [4].

x + 2 ω y = u_x ;

y – 2ω x – 3ω ² y = u_y ;

z + ω2z = uz, где x, x, x — относительная дальность центров масс корабля и станции, скорость и линейное ускорение ее изменения; y, y, y — относительное высотное отклонение центров масс корабля и станции, скорость и линейное ускорение его изменения; z, z, z — относительное боковое отклонение центров масс корабля и станции, скорость и линейное ускорение его изменения; ux, uy, uz — приращения ускорений от управляющих воздействий в каналах относительной дальности, высотного и бокового отклонений, соответственно; ω = 1,131·10–3 рад/с — орбитальная угловая скорость корабля.

Найдем аналитическое решение исходной системы в форме Коши и запишем его в конечно-разностном виде с шагом сетки h = t_{n + 1} – t_n = 0,2 с, который был выбран равным такту работы бортового компьютера.

_X прод-попер _{= L X} прод-попер _{+ U} прод-попер _; n + 1                 n                 n

Xnпрод-попер = (x, x, y, y, z, z)nT, где L — линейный оператор во введенной орто-нормированной системе координат; Unпрод-попер — вектор управляющего воздействия в канале продольно-поперечного движения.

В свою очередь выпишем матрицу L переходных процессов:

	<	4
	1	ω sinω h - 3 h	6ωsinω h - 6ω h
	0	4cosω h - 3	-6ω(1 - cosω h )
	0	2 ω (1 - cosω h )	4 - 3cosω h
L =
	0	2sinω h	3ωsinω h
	0	0	0
	0	0	0

2 ω (1 - cosω h )	0	0
-2sinω h	0	0
sinω h	0	0
ω
cosω h	0	0
0	cosω h	sinω h
		ω
0	-ωsinω h	cosω h

где h = 0,2 с — такт работы бортового компьютера.

В рамках задачи причаливания оператор L — это постоянная матрица, что достигается допущением сферичности Земли и отсутствием учета наклонения орбиты. Однако при введении неучтенных параметров задача нахождения бортовой модели перестает быть линейной. Построение адаптивного наблюдателя на основе предложенной модели осложняется расчетами и без того загруженным бортовым компьютером. Здесь особенно стоит отметить, что искомая бортовая модель прогнозирует параметры относительного движения каждые 0,2 c, что вполне достаточно для достижения заданной точности причаливания.

Угловое движение корабля вокруг его центра масс

Без ограничения общности будем считать, что станция поддерживает свою ОСК, т. е. связанная система координат (ССК) и ОСК станции полностью совпадают. Таким образом, в рамках нашей задачи угловое движение корабля вокруг своего центра масс можно представить как вращение твердого тела вокруг осей орбитальной системы координат (ОСК корабля или ОСК станции).

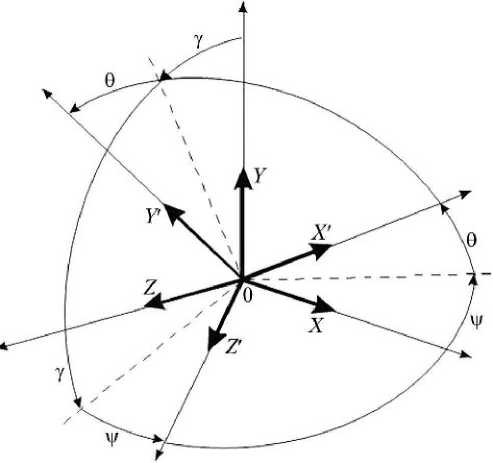
Рис. 2. Угловое движение объекта управления вокруг его центра масс

Вращение абсолютно твердого тела в пространстве может быть представлено тремя последовательными поворотами связанных с главными моментами инерции корабля осей OX′, OY′ и OZ′ вокруг осей OX, OY и OZ ОСК, а именно: по крену γ, тангажу ψ и рысканию θ (рис. 2).

Jy – Jz      Jx + Jy – Jz

γ = 4ω ² J γ – ω J      ψ + u _γ ;

x               Jx

ψ = ω ²

J_x – J_z ψ + ω

Jy

J x + J y – J z

J y

γ + u _ψ ;

θ = 3ω2 Jy – Jxθ + uθ, Jz где Jx, Jy, Jz — главные моменты инерции корабля в связанной с ним системе координат; uγ, uψ, uθ — приращения угловых ускорений от управляющих воздействий в каналах углового движения корабля вокруг его центра масс по крену, тангажу и рысканию, соответственно.

При малых углах такой разворот аналогично продольно-поперечному движению может быть описан шестью линейными уравнениями в конечно-разностном виде, аналитическое решение которых также представляется в конечно-разностном виде.

_X вращ _{= R X} вращ _{+ U} вращ _;

n + 1            n            n ^;

Xnвращ = (γ, γ, ψ, ψ, θ, θ)nT, где γ, γ — угловое положение корабля относительно стыковочного узла станции по крену и его угловая скорость по крену; ψ, ψ — по тангажу и θ, θ — по рысканию, соответственно.

Матрица R переходных процессов вращательных компонент вектора-состояния в приближении первого порядка выглядит следующим образом:

0 1 0 0 0 0 Jx + Jy – Jz 4to2 y' Jx 0 0 -to---------'------- Jx 0 0 R=I„. + h 0 0 Jx + Jy – Jz 0 Jx – Jz 1 0 0 0 to----------------- Jy to2----------- Jy 0 0 0 0 0 0 0 0 3to2 J y- J x Jz 1 0 4 0 0 0 0 где I6×6 — единичная матрица размерности шесть.

Также стоит отметить, что матрица переходных процессов R для углового движения объекта управления вокруг его центра масс зависит от практически постоянных величин: такта бортового компьютера h, орбитальной угловой скорости ω и компонент тензора инерции J корабля. То есть, матрицу R, как и матрицу L, также условно можно считать постоянной.

Упругие колебания конструкции

Динамика конструкции корабля в настоящей работе представлена одним доминирующим тоном упругих колебаний с частотой ω ₁ = 0,3 Гц и логарифмическим декрементом затухания ξ = 0,05. Рис. 3 схематично иллюстрирует влияние формы доминирующего тона на угловое движение штанги, на конце которой расположена приемо-передающая антенна локатора аппаратуры «Курс».

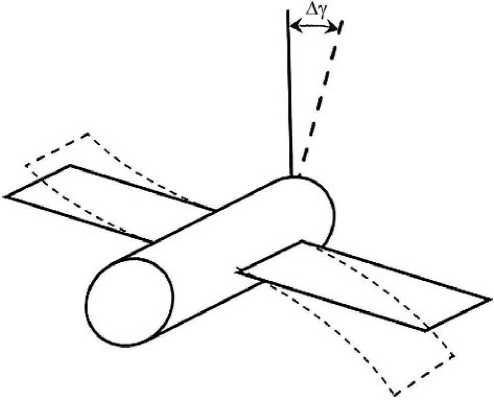
Рис. 3. Упругие колебания конструкции корабля

Примечание. Δ γ — угол поворота штанги.

Исходя из вышеописанных результатов натурных испытаний, движения штанги могут быть описаны неоднородным линейным уравнением затухающих гармонических колебаний:

Δγ +2ξω1Δγ + ω21Δγ = fΔγMx, где ω1 — циклическая частота упругих колебаний конструкции; ξ — логарифмический декремент затухания; fΔγ — коэффициент усиления колебательной угловой скорости крена; Mx — моменты импульса ДПО для поворота корабля вокруг продольной оси.

Общее решение неоднородного уравнения, как известно, складывается из какого-либо из его частных решений и общего решения данного однородного уравнения. Запишем решение уравнений колебаний для угла поворота штанги Δγ и ее угловой скорости Δγ в конечно-разностном виде:

(ΔΔγγ) n + 1 = H ( ΔΔγγ) n + ( fΔγ M0xh)n, где H — матрица переходных колебательных процессов; fΔγMxh — приращение угловой скорости колебаний штанги в результате включения импульса длительностью h = 0,2 c.

Выпишем матрицу переходных процессов для колебательных компонент вектора состояния:

H = e ^{– ξω 1 h}

( cosω ₁ h –ω ₁ sinω ₁ h

sinω ₁ h ω ₁ cosω ₁ h

)

При включении корректирующих двигателей ориентации в канале крена происхо- дит раскачивание упругих колебаний конструкции вокруг продольной оси корабля. Момент сил, возникающий при включении двигателей стабилизации корабля по крену, поворачивает штангу, придавая ей при этом угловую скорость.

Измерения

Для физической простоты поставленной задачи будем считать аппаратуру системы «Курс» совокупностью лазерного дальномера и двух уголковых отражателей:

_Y Курс

^Y n ⁼ ( _Y ТИУС ) .

В канал измерений поступают: относительная дальность между концами антенн, скорость измеренной дальности, углы пеленга бокового и высотного отклонений, и, соответственно, их угловые скорости. Такое допущение в общем случае не позволяет найти линейную зависимость вектора измерений относительно вектора состояния корабля, а именно — матрицу наблюдателя C . Однако данное обстоятельство никоим образом не мешает найти аналитическую зависимость компонент вектора измерений Y _n от компонент вектора состояния X _n , исходя из геометрии расположения антенн «Курс» корабля и станции.

x – x _A + x _П

/

ρ

.

ρ

_Y Курс n

ε

ε z

.

ε

z

V у n

x.

z – ∆γ y _A ^ρ

^{. – ∆ . y} A ^{ρ y}

= C ( X n );

ρ

. y

ρ

Xn = (x, x, y, y, z, z, γ, γ, ψ, ψ,θ, θ, Δγ, Δγ)nT, где xА, yА, xП — расположение концов антенн дальномеров «Курс» у корабля (Курс-А) и станции (Курс-П) в их связанной системе координат.

Показания волоконно-оптического ТИУС определяют ориентацию связанной (с главными моментами инерции) системы координат корабля относительно орбитальной системы. Погрешности значений показаний ТИУС находятся в области допустимых значений и не нуждаются в применении фильтра Калмана.

При сближении корабля со станцией интенсивность шумов в измерительных каналах из-за переотражений возрастает. На основании анализа телеметрической информации шумы измерений, обусловленные переотражением радиосигналов от элементов конструкции станции, на каждом такте бортового компьютера можно аппроксимировать возрастающим по гиперболическому закону нестационарным белым гауссовым шумом ν _{2 n} :

^Y n = C ( X n ) + V 2 n .

Важно отметить, что включение реактивных двигателей малой тяги — двигателей причаливания и ориентации (ДПО) — в канале крена возбуждает упругие колебания конструкции корабля. Данное явление учитывается в матрице управления B .