Применение физической модели сферолитно-решеточной структуры при прогнозировании прочности цементного камня и бетона

В развитие теоретических представлений о структуре цементного камня и бетона автором была предложена сферолитно-решеточная модель структуры цементного камня. Для проверки действительности данной модели как физической модели структуры матричного компонента цементных композитов было принято решение о проведении аналитических и экспериментальных исследований по вопросу о применимости данной модели в прогнозировании прочности.

При рассмотрении различных видов упаковки цементных образований в сферолитно-решеточных моделях (табл. 1) можно выделить 2 основных элемента, определяющие механические свойства структуры: сферолитные гидратные образования и межгидратное пространство в виде макрокапил-лярных пор с гидравлическим радиусом.

Поскольку макрокапиллярные поры являются непрерывной системой и распространяются в направлении отсутствия твердой фазы, а трещины распространяются в направлении разрыва сплошности, макрокапилляры не могут являться направлениями распространения трещин при разрушении под действием механической нагрузки. Вместе с тем очевидно, что прирост макрокапиллярной и общей пористости приводит к снижению плотности и, следовательно, прочности структуры. Для выявления механизма влияния структурной плотности на прочность гидратной структуры требуется проанализировать модель сферолигно-решетчатой структуры, выделить связи и предложить расчетную физическую модель прочности при сжатии.

С позиции механизма разрушения нарушение целостности при нагружении возникает вследствие растягивающих напряжений, возникающих перпендикулярно направлению приложения нагрузки. Следовательно, разрушение связей обусловлено в горизонтальных связях между сферолитами в модельной решетке. Данный тип нагружения относится к растяжению при изгибе, а, следовательно, пространство под связью или размер макрокапилляра будет определять опорную базу сростка сферолитов.

Выделим сечения межопорного пространства в сферолитно-решеточных структурах с различной структурной плотностью. Упаковки различной степени уплотнения приведены в табл. 1.

В результате данные сечения обладают приведенным радиусом и могут быть представлены в виде ячейковых пор. Таким образом, цементный камень модельно с позиции прочности при условии постоянной прочности связи между сферолитами можно рассматривать как условно-ячеистую структуру.

Рассмотрим расчетную модель прочности цементного камня на базе модельной ячеистой

Таблица 1

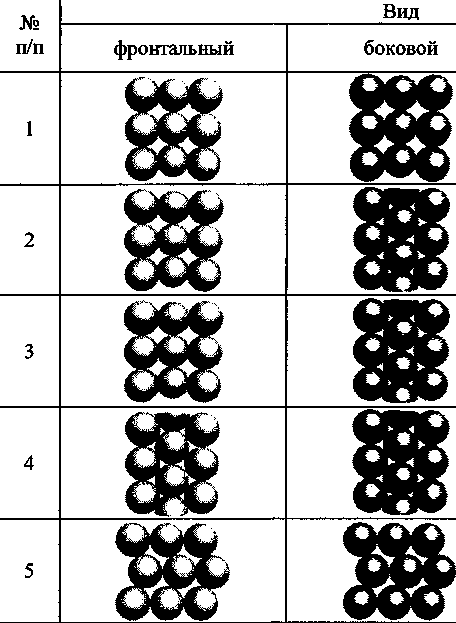
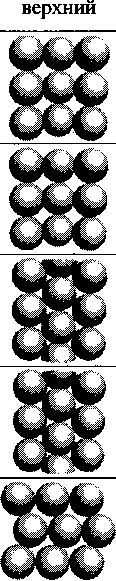
Выделенное сечение межзерновой пустоты (макропора)

структуры. Общеизвестно, что прочность ячеистой структуры зависит от прочности межпоровых перегородок и общей пористости (плотности). Для составления математической модели прочности ячеистой структуры был выдвинут ряд тезисов:

• -    прочность ячеистой структуры равна сумме прочностей гидратных оболочек элементарных ячеек в количестве, приходящемся на нагружаемую площадь;

• -    прочность элементарной оболочки равна прочности при изгибе твердой перегородки между ячейками;

• -    перегородка может быть представлена в виде балки с двухопорной схемой нагружения с переводным коэффициентом к, учитывающим арочное строение перегородки (рис. 1).

Предложенная расчетная модель сводится к решению системы уравнений, в котором прочность при сжатии ячеистой структуры может быть выражена как отношение максимальной нагрузки к площади элементарной несущей ячейки.

d опер -^^max** _ -'^’max . ^юг 2nd5²    2n8² ’

N d _ max

n(d + 3)

где R^ - предел прочности при изгибе перегородки элементарной ячейки; R^ - предел прочности при сжатии образца ячеистого бетона; W_max -максимальная разрушающая нагрузка образца;

Выделенное сечение ячейковой макропоры

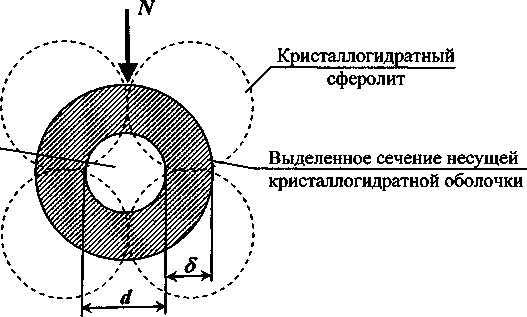
Рис. 1. Схема нагружения элементарной ячейки

d - средний диаметр элементарных пор; б - толщина межпоровой перегородки; п - количество элементарных пор на единице площади поперечного сечения; к - коэффициент, учитывающий кривизну изгибаемой поверхности.

Выразив из первого уравнения К_та и под

ставив его во второе можно получить следующую зависимость:

^сж

2@L

3k(d+6)2 ‘

Толщину межпоровой перегородки можно определить из условия:

у где Кг - объем гидратной составляющей в образ

це; S_w - удельная поверхность макрокапилляр-

ных пор образца.

у V V d g _ ^Г Г  __________ ^У V^й

YUtd²       ^2 6РУ_Ж’

Ttd3,6

Формула для определения прочности при сжатии цементного камня примет следующий вид: 27^(0,32 + 0,42а)2 /<   =----------------------------_. ф               1/1

ЗА(0,32 + 6В/Ц-2,1а)2

При а = В/Ц + 0,28 _ 2С? (0,44+ 0,42 В/Ц)^{2 сж}     3^(4,9 В/Ц-0,27)²   '

Выражение в числителе назовем фактором гидратации, а выражение в знаменателе - фактором пористости.

После вывода за скобки всех постоянных в числителе и знаменателе и коррелирования получена следующая зависимость прочности цементного бетона при сжатии

0,082^(1 + 0,95В/Ц)2 (В/Ц-0,055)2    ’             ( J

где Р - макропористость материала; К_цк - объем

цементного камня в естественном состоянии.

При К_ж = 1

э 7?пеРгл 2

D _ Т13Г ^г Г

Зк^Р + У,)2 ■

При Иг=1-Р

= 2@L-P)^ сж   ЗЛЦ + 5Р)2 ‘

По [1] _P=W^.

0,32 + В/Ц

где R^ - активность вяжущего, МПа.

В табл. 2 приведены сравнительные фактические и расчетные данные прочности при сжатии цементного камня на основе ШПЦ 400, ПЦ 400Д-20 и ПЦ 500 Д-0 различных заводов.

Сравнение расчетных и фактических данных прочности показывает сходимость 90 и более % в 80 % случаев. Коэффициент корреляции полученной зависимости составляет 0,92.

Моделирование и математический анализ прочности цементных композитов проводились на основе учета степени переменности поровой структуры матричного компонента.

Расчетная модель механических свойств такого композита, исходя из разработанной модели цементного камня, представляет собой ячеистую структуру с переменной плотностью в одном направлении, за счет послойного изменения содер-

Таблица2

Завод-изготовитель Марка цемента Активность цемента Rp, МПа НГ, % Фактическая Re» цементного камня, 28 сут, МПа Расчетное значение прочности, МПа Отклонение от фактич. значения, % Невьянский ПЦ500Д0 43,8 25 128,7 141,12 9,65 ПЦ400Д20 32,6 25,25 95,7 102,78 7,40 ШПЦ400 38,8 24,5 120,1 130,67 8,80 Горнозаводский ПЦ500Д0 47,2 27,5 137,8 124,10 -9,94 ПЦ400Д20 38,9 28,5 100,5 95,00 -5,48 Коркинский ПЦ500Д0 47 25 139 151,43 8,94 ПЦ400Д20 38,1 24,75 115,3 125,48 8,83 ШПЦ400 29,7 26 87,3 87,92 0,71 Сухоложский ПЦ500Д0 42,1 23,75 120,6 151,90 25,95 ПЦ400Д20 35 26,25 108,2 101,51 -6,18 ШПЦ400 30,4 30,75 69,3 63,69 -8,10 Катав-Ивановский ПЦ500Д0 51,7 25 151,1 166,57 10,24 ПЦ400Д20 45,2 25,25 134,3 142,51 6,11 ШПЦ400 42,2 24,5 132,5 142,12 7,26 жания пор в объеме материала при неизменном составе матричного компонента (рис. 2).

Рис. 2. Схема распределения пор в образце с переменной структурой

Такую структуру недостаточно характеризовать средней величиной структурной плотности

£> = 15™l±5i2,                     (Ю)

но необходимо приводить характеристику степени ее переменности:

_(|1) ^пер D D

Экспериментальные исследования показали, что разноплотные слои в составе одного образца при нагружении работают раздельно, т. е. более легкие слои при превышении их несущей способности сминаются, откалываются и вся нагрузка прикладывается на самые плотные слои. При возрастании степени переменности толщина несущего слоя пропорционально сокращается. Таким образом, переменную ячеистую структуру можно условно разделить на пористый и плотный слои (рис. 3). С целью получения достоверных результатов предела прочности при сжатии испытания образцов вариатропного бетона должны проводиться одним из следующих способов: одновременным испытанием двух образцов или испытанием одного образца между заклиненными плитами пресса.

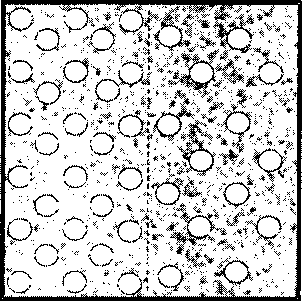
Рис. 3. Схема условного распределения пор по объему образца для математического моделирования. Справа - уплотненный слой (пл), слева - разуплотненный (л)

Учитывая неравномерность распределения матричного компонента по объему, и как следствие неравномерность воспринимаемой нагрузки, прочность бетона с переменной структурой определяется прочностью слоя с плотностью, превышающей среднюю плотность образца:

N

Явар—ЯнЛс, (12)

где N - разрушающая нагрузка; R^ - прочность плотного слоя; 5_ПЛ - площадь плотного слоя; ^пс ⁼^'пл/‘5' ~ коэффициент уплотненного слоя (отношение площадей плотного слоя и образца.

Апробация полученной расчетной модели была проведена экспериментально путем создания вариатропных и однородных образцов цементного полистиролбетона, в котором роль ячеек выполняли гранулы невспученного полистирола фракции 0,315... 1,25 мм. Поскольку в модельном эксперименте невозможно создать плавное изменение плотности по сечению образца, создание переменной структуры обеспечивалось послойной заливкой единичных слоев различной средней плотности. Таким образом были получены образцы размером 7,07x7,07x7,07 с шестью слоями, причем плотность каждого последующего слоя была больше предыдущего. Шаг изменения плотности задавался исходя из требуемого по эксперименту коэффициента переменности. Плотность слоя регулировалась расходом цемента. В результате была получена зависимость коэффициента слоя и прочности образцов в возрасте 28 сут от степени переменности структуры бетона.

Испытания подтвердили, что структура с переменной плотностью может быть разделена на 2 слоя с позиции поведения под нагрузкой - на жесткий и деформативный, с точки зрения плотности -плотный и пористый. И с позиции прочности и с позиции плотности свойства лимитируются объемом и свойствами плотного слоя. По экспериментальным данным получена математическая зависимость коэффициента плотного слоя (коэффициент корреляции 0,98):

^==^- = 1-со8[1,57(1-^ер)]. (13)

Полученная зависимость показывает возможность повышения прочностных свойств бетона на 20...25 % при формировании переменной поровой структуры со степенью переменности 0,3...0,5. Таким образом, переменная структура при сопротивлении проявляет неоднородность, однако формирование переменной структуры, за счет повышенных свойств плотного слоя, является эффективным направлением повышения качества цементных композитов.

При рассмотрении рядовых цементных композитов структура матричного компонента может быть уподоблена переменной структуре, так как пористость у поверхности заполнителя в разы пре- вышает пористость центрального слоя цементного камня. При рассмотрении заполненных композитов в качестве факторов переменности вместо плотности можно применить показатель В/Ц-отношения.

(В/Ц—НГ) НГ пер в/ц в/ц ’

тогда

(В/Ц-В/Ц^) ^пер в/ц

,     ,       , НГ

£пс — 1 —cos 1,57—;— .

пс 1_ в/ц

Прочность композита с переменным распре-

Таблица 3

Rc=R™^=^nc- (17)

Тогда прочность при сжатии цементного композита составит

0,08К1(1+0,95НГ)2С

"---------о---- 1 - COS

(НГ-0,055)2   (

НГ

В/Ц

;(18)

_к _ Уп= _ (1 + 0,95НГ)²(В/Ц-0,055)²

R   ^   (НГ-0,055)2(1 + 0,95В/Ц)2

• f,     Г ,_ НГ

х 1-cos 1,57—— .

I     L   в/uJJ

Были определены расчетные и фактические показатели прочности при сжатии бетонов (табл. 3)

на основе портландцементов марок ПЦ 400 Д-20, ШПЦ 400 и ПЦ 500 Д-0 Коркинского, Сухоложского, Невьянского, Катав-Ивановского и Горнозаводского заводов при различных значениях В/Ц (более 45 составов), которые продемонстрировали высокую сходимость - в 90 % случаев ошибка составляет менее 15 %. Коэффициент корреляции новой зависимости составляет 0,88.

Графический вид зависимости для бетона на ПЦ 400 Д-20 Коркинского завода приведен на рис. 4.

Согласно приведенной зависимости, введение заполнителя в состав композита позволяет обеспечить прирост прочности в диапазоне наиболее часто применяемых В/Ц = 0,4...0,6 от20 до 50 %, особенно в композитах с небольшими расходами цемента. Таким образом, управление переменностью при обеспечении направленного формирования плотного слоя матричного компонента является

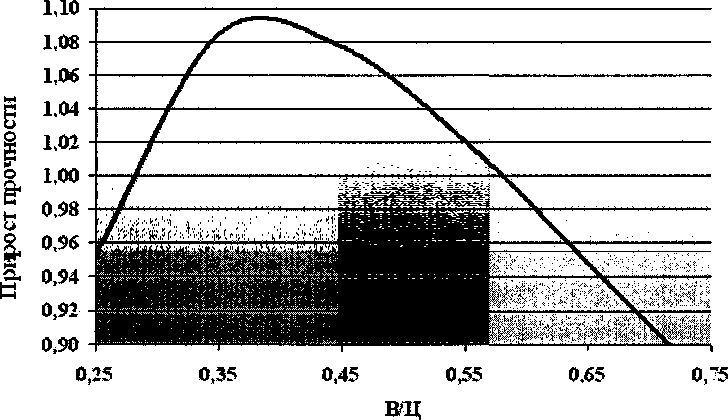
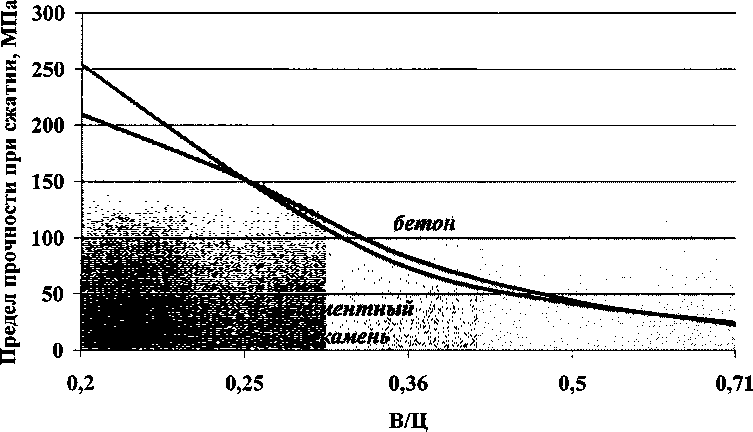
Рис. 4. Расчетные зависимости прироста прочности и прочности при сжатии цементных композитов относительно цементного камня с равномерно распределенным водосодер-жанием (для ПЦ 400-Д20 Коркинского завода)

эффективным направлением повышения качества цементных композитов.

При введении поверхностно-активных веществ эффект гидравлического самоуплотнения может быть увеличен, а его прирост оценен согласно предложенной зависимости путем учета снижения нормальной густоты цемента или прироста В/Ц у поверхности заполнителя.

Прирост прочности при введении пластификатора составит k пл = R™ = (1 + 0,95(1 - *ред )НГ)2 (НГ - 0,055)2 *

R R   ((1-^реД)НГ-0,055)2(1 + 0,95НГ)2

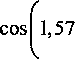
НЖ

В/Ц ,

, I с НГ 1-COS 1,57—;—

I В/Ц.

где A^ - водоредуцирование при введении пластификатора.

. Выводы

• 1.    Получена адекватная математическая зависимость прочности цементного камня и бетона от основных факторов состава на базе физической модели сферолитно-решеточной структуры цементного камня.

• 2.    Предложены математические основы учета неоднородности строения поровой структуры матричного компонента цементного композита, на основе которых можно определить предел эффективности снижения В/Ц при получении высокопрочных бетонов.