ПРИМЕНЕНИЕ ФИЗИЧЕСКОЙ ЗАДАЧИ АТЕЛКАК ОСНОВЫ ДЛЯ ВИЗУАЛИЗАЦИИ СТРУКТУРЫ ВЗАИМОСВЯЗЕЙ МЕЖДУ ОБЪЕКТАМИ СТАТИСТИЧЕСКОЙ СИСТЕМЫ

Рассмотрен метод визуализации структуры взаимосвязей между объектами статистической системы, основанный на модификации физической задачи N тел. Поставлена и решена задача получения новой формы визуального представления структуры взаимосвязей в виде пузырьковой диаграммы.

При рассмотрении сложных статистических систем, состоящих из множества объектов, для анализа структур заложенных в них взаимосвязей в качестве отправной точки часто используются матрицы расстояний (близости, взаимосвязанности) между объектами, получаемые путем введения той или иной метрики по ее определению. Такие матрицы, по сути, являются набором многомерных данных характеризующих взаимосвязи между объек тами системы.

В качестве одного из подходов к разработке методов визуализации общей структуры взаимосвязей, являющейся содержательной основой таких матриц, может быть предложено использование модификаций математической модели, описывающей физическую задачу N тел. Отметим, что математическая модель физической задачи N тел описывается системой нелинейных дифферен циальных уравнений второго порядка:

d2 r mi     i dt2

N

= "I Г j = i 11

m i m

i = 1, N .     (1)

r ^- r

В работе [1] сформулирована задача N случайных со- бытий как своеобразный прототип физической задачи N тел, основанный на метрической интерпретации ковариации статистической зависимости случайных событий и понятии силы статистического взаимодействия. Задача N случайных событий может быть представлена, как задача Коши поиска решения системы дифференциальных уравнений второго порядка при заданных начальных условиях:

^P ( z ) d r = -^ For zz' [ rz - r z ']) , ⁽²⁾ dt z'

где z = s -f- здесь x еК - произвольное событие из L x , конечного множества К , xc - его дополнение; z e Z , здесь Z = К U Кc - множество, содержащее все события и их дополнения, соответствующее конечному множеству К ;z'- все события из множества Zза исключением одного из событий z, силовое взаимодействие которого с событиямиz' описывает соответствующее уравнение системы; P(z) - вероятность наступления события z; , P ( z ) P ( z')

For zz, = —- - сила статистического

P ( z ) + P ( z ) - 2 P ( z 1 z )

парного взаимодействия случайных событий z и z'. г -вектор координат события z на визуализационной плоскости А ² .

Численное решение этой задачи используется в качестве метода динамической визуализации взаимодействий в статистических системах, который каждой такой системе сопоставляет ее динамический образ в виде орбитальной структуры силового взаимодействия случайных событий на визуализационной плоскости - динамической визуализации матрицы сил взаимодействий случайных событий, или, что эквивалентно, при некоторых преобразованиях ковариационной матрицы случайных событий.

В качестве другого подхода к визуализации структуры взаимосвязей объектов статистической системы, представляемой симметричной матрицей взаимосвязей, который также основан на модификации задачи Ател, может быть предложена визуализация в виде специальной пузырьковой диаграммы - диаграммы, изображаемой в евклидовой плоскости, на которой объектам системы соответству- ют пузырьки различного диаметра, а связям между объектами - взаимные расстояния между пузырьками.

Решение задачи. Обозначим объекты статистической системы как и элементов, составляющих некоторое множество А = {а₁, а₂, ... , а_п }.Симметричную матрицу взаимосвязей между объектами системы (ковариационную матрицу или, возможно, иную матрицу связей), которая подлежит визуализации, обозначим матрицей С размерностью и • и. Содержание матрицы будут составлять количественные значения соответствующих связей, преобразованные и отнормированные к интервалу [0; 1].

Определим диаметры пузырьков как некоторые положительные веса элементов w . (. = 1, ..., и).

Будем наносить на диаграмму квадратную сетку с шагом L = max{w₁, .., wj, обозначающую предельно малое расстояние между пузырьками, интерпретируемое как нулевая связь между элементами, которым они соответствуют

Найдем зависимость необходимого расстояния между пузырьками на диаграмме от уровня связи между элементами, которым они соответствуют: d = (1 - c.^L £ [0; L]. Соответственно расстояние между центрами пузырьков будет определяться формулой dc . ■= (1 - c_y)L+0,5(w. + w) £ [0; L + 0,5(w . + w)]. Такое определение расстояния между пузырьками является интуитивно понятным и удобным для визуального восприятия и оценки связи между элементами, которым они соответствуют: чем меньше расчетное расстояние между пузырьками (вплоть до нулевого), тем ближе значение соответствующей связи к единице, и наоборот. Определим свод расстояний dc между всеми центрами имеющихся пузырьков в виде симметричной матрицы расчетных расстояний DC размерностью и • и.

Моделирование силового взаимодействия и построим математическую модель: определим закономерности силового взаимодействия пузырьков таким образом, чтобы оно обеспечивало их автоматическое стремление установиться на расчетное для каждой пары расстояние. Для этого может быть предложено моделирование ситуации, при которой пузырьки взаимодействуют таким образом, как будто каждая из возможных пар закреплена на концах пружины, размер которой в недеформированном состоянии соответствует расчетному для пузырьков расстоянию dc и любая ее деформация приводит к тому что пружина пытается вернуться в недеформированное состояние.

В соответствии с законом Гука, при малой деформации сила упругости определяется по формуле F x = - kx , где к- коэффициент жесткости пружины (коэффициент пропорциональности); х - положение конца пружины на оси А' равное нулю при недеформированном состоянии пружины.

По аналогии с силой упругости определим силу описанного выше парного взаимодействия пузырьков. Для этого примем коэффициент пропорциональности (упругости) равным произведению весов взаимодействующих пузырьков (элементов рассматриваемого множестваА): к = ww. Такое определение коэффициента к позволит учесть при моделировании процесса взаимодействия то, что пузырьки, обладающие большим весом, потенциально смогут оказывать более сильное силовое воздействие.

Найдем смещение пузырьков относительно расчетного расстояния dc. ^ (растяжение или сжатие пружины), приняв, что центру каждого из пузырьков с диаметром w . на диаграмме соответствует некоторая точка с координатами г. Тогда для одномерного пространства вектор силы (без учета коэффициента пропорциональности), действующей на пузырек. при его взаимодействии с пузырьком j -х ~ (| г . - г^\ - dc). Для пространства произвольной размерности при разложении вектора силы по осям -х ~ (| г . ^- rj ^{- dc},._y ⁾⁽r. ^- Г ^|Z| Г. ^-гф

Таким образом, сила, воздействующая на пузырек . при его взаимодействии с пузырькому (с учетом особенностей взаимодействия пузырьков, соответствующих невзаимосвязанным элементам), определяется следующей зависимостью:

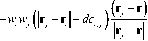
ECX0

0, scX0 dc _tj = L + 0,5 ( w , + w j ) 0 |r j - r| <  dc , j .

Fi , j =

dc _t j £ [ L + 0,5 ( w i + W j ) ) 0X0

[ dc , j. = L + 0,5 ( w ,

j ) )^{0 r} - - ^rl <  dc j - J (3)

При определении силы взаимодействия делается предположение, что центры пузырьков не могут совпасть.

Составим математическую модель системы взаимодействующих пузырьков на основе системы (1), описывающей задачу N тел, подвергая ее следующим изменениям:

• -    массы тел заменим весами элементов;

• -    физическую силу взаимодействия между телами заменим силой парного взаимодействия пузырьков (3).

В результате получим следующую систему нелинейных дифференциальных уравнений второго порядка, описывающую модель силового взаимодействия N пузырьков:

d ² r w

‘ dt ²

N

= — £ ww

I Г '^-

i = 1, N .(4)

j = 1 j * ,

В соответствии с зависимостью (3), на систему так- же накладывается дополнительное условие; при равенстве расчетного расстояния пороговому расстоянию нулевой связи (dc, . = L + 0,5(w. + w)) и при достижении соответствующими пузырьками такого расстояния друг относительно друга сила взаимодействия между ними равна нулю (пузырьки соответствуют несвязанным элементам). Это позволяет предотвратить излишнюю скученность пузырьков на диаграмме, не ухудшая при этом ее наглядности (например, в частном случае, когда все коэффициенты взаимосвязей равны нулю, пузырьки просто «разлетятся» на расстояние, большее или равное шагу сетки, а ни будут пытаться сохранить его во что бы то ни стало, образуя при этом определенную скученную группировку).

Основное отличие полученной системы от ее физического оригинала состоит в природе действующих сил:

• -    в физической системе (1) с увеличением расстояния между телами сила их парного взаимодействия уменьшается;

• -    в измененной системе чем больше расстояние между пузырьками отличается от рассчитанного для них в матрице расстояний DC, тем больше будет величина силы взаимодействия между ними, стремящейся установить пузырьки в положение, при котором расстояние между ними станет равно расчетному (dc , )

  Упростив систему (4), получим:

  
  

  d 2 r              _{_____}

  = Ф , .( г ), i = 1, N ,                   ⁽ 5 ⁾

  
  

  N где ф ( r ) = - £

  
  

  j = 1 j * i

  
  

  w j

  
  

  ^- r j

  
  

  (

  
  

  ) 1

  
  

  dc i , j

  
  

  _-

  
  
  
  

  последних итерациях удовлетворяет предварительно заданному необходимому значению невязки.

  Основываясь на сопоставлении перемещения пузырьков за один шаг в соответствии с законами взаимодей

  
  

  7J

  
  

  Общее решение задачи сводится к нахождению ста

  
  

  ционарной точки для системы дифференциальных уравнений, в которой взаимное расположение пузырьков будет таким, что их ускорения и скорости будут равны нулю, т. е. взаимное силовое побуждение к дви

  
  

  ствия, заложенными в систему, и того перемещения, которое им необходимо сделать для установления на расстояния в соответствии с матрицей DC, можно аналитически определить итерационный параметр т , обеспечивающий основу успешности решения задачи - сходимость

  
  

  этого параметра:

  
  

  т =

  
  
  
  

  жению отсутствует, так как все силы взаимодействия уравновешены):

  
  

  N I W . i = 1

  
  

  = const.

  
  

  Ф ( г ) = 0.

  С физической точки зрения эта система описывает набор взаимодействующих пузырьков в евклидовом пространстве, в котором отсутствует сопротивление среды и нет никаких сил, кроме сил взаимодействия пузырьков. Стоит отметить, и то, что из физики известно, что связь между силой действующей на тело и его потенциальной энергией определяется формулой

  
  

  Рассмотрим применение разработанного алгоритма

  
  

  в качестве финансового инструмента визуального представления корреляций курсов, входящих в портфель ак

  
  

  ций.

  
  

  Для составления портфеля акций и получения данных о его характеристиках использовался финансовый портал, разработанный компанией «РЭА-Риск-Менедж-

  
  

  F = -grad W , где grad^- градиент скалярной функции потенциальной энергии.

  Правая часть системы (4), на которой базируется решение поставленной задачи, по сути, описывает воздействие всех сил, которые действуют на каждый из пузырьков в рамках рассматриваемой системы. Таким образом, можно сказать, что искомая стационарная точка соответствует минимуму функции потенциальной энергии системы как целевой минимизируемой функции.

  Поставленная задача может быть решена с помощью одношагового метода простой итерации:

  Г * ¹ = r ^t + T F ( r ^t ), где: г * - вектор координат пузырьков на k-м шаге; T - итерационный параметр.

  Расчет начинается с начального положения пузырьков r ⁰. На каждой новой итерации скорости пузырьков равны нулю, а новое значение их координат находится как сумма текущих значений координат и координат векторов ускорений, взятых с коэффициентом т и определяемых при текущем расположении пузырьков. Расчет останавливается, когда изменение координат пузырьков на

  
  

  мент», с помощью которого можно рассчитать доходность, риск (волатильность) и корреляцию курсов акций на основе их котировок, импортируемых в режиме реального времени с биржевых площадок. Эти показатели обязательно учитываются при управлении портфелем. В частности, волатильность акции, как и ее доходность, может изменяться во времени и не являться постоянной величиной, поэтому существует необходимость периодически переоценивать портфель и изменять его структуру. Одной из сторон анализа структуры портфеля является взаимная корреляция курсов входящих в него акций. Так, например, большая степень общей коррелирован-ности курсов акций портфеля, являющаяся возможным

  
  

  следствием различных экономических, политических и (или) других процессов и явлений внутренней и внешней среды компаний, указывает на уменьшение степени диверсифицированности капитала, вложенного в портфель (с точки зрения обобщенных колебаний его котировок) и, соответственно, не увеличение степени его инвестиционного риска.

  Используя финансовый портал компании «РЭА-Риск-Менеджмент», был сформирован портфель из акций десяти известных компаний (см. таблицу).

  Затем на основе данных за месяц была получена корреляция курсов соответствующих акций на фондовой

  
  

  Коды и наименования компаний на фондовой бирже

  Коб коцпанбб на фондовой обрже	Набценованбе коцпанбб
  AFLT	«Аэрофлот»
  EESR	«РАО ЕЭС»
  LKOH	«ЛокойХ»
  MSNG	«Мосэнерго»
  RTKM	«РостеХекоц»
  SBER	«Саераанк»
  SIBN	«Сбонефть»
  SNGS	«Сорготнефтегаз»
  TATN	«Татнефть»
  YUKO	«Юкос»

  
  

бирже Российской торговой системы (РТС) представленная следующей корреляционной матрицей:

	AFLT	EESR	LKOH	MSNG	RTKM	SBER	SIBN	SNGS	TATN	YUKO
AFLT	1,00	-0,15	0,00	-0,21	0,01	-0,14	0,40	0,26	0,12	0,07
EESR	-0,15	1,00	0,05	0,12	-0,42	-0,05	0,01	0,26	0,16	0,23
LKOH	0,00	0,05	1,00	-0,08	0,38	0,16	0,67	0,49	0,48	0,63
MSNG	-0,21	0,12	-0,08	1,00	-0,46	-0,25	-0,24	-0,40	-0,05	0,07
RTKM	0,01	-0,42	0,38	-0,46	1,00	0,28	0,19	0,13	0,10	-0,12
SBER	-0,14	-0,05	0,16	-0,25	0,28	1,00	0,26	0,20	0,29	0,35
SIBN	0,40	0,01	0,67	-0,24	0,19	0,26	1,00	0,66	0,46	0,67
SNGS	0,26	0,26	0,49	-0,40	0,13	0,20	0,66	1,00	0,43	0,34
TATN	0,12	0,16	0,48	-0,05	0,10	0,29	0,46	0,43	1,00	0,36
YUKO	0,07	0,23	0,63	0,07	-0,12	0,35	0,67	0,34	0,36	1,00

Примечание. Жирным шрифтом выделены корреляции, для которых была проведена визуализации.

Результат работы описываемого в данной статье алгоритма, в соответствии с полученной матрицей, визуализирован в виде пузырьковых диаграмм положительной и отрицательной корреляционной структуры связей (см. рисунок). Визуализация проведена для корреляций лежащих в диапазонах [-1; -0.4] и [0,4; 1]. Полученная диаграмма значительно более наглядно представляют структуру взаимосвязей котировок акций, заложенную в корреляционной матрице, чем сама матрица. Диаграмма дает возможность биржевым аналитикам получить информацию в удобной и легко воспринимаемой визуальной форме для проведения анализа особенностей взаимного и общего поведения котировок акций портфеля и принятия возможных решений относительно изменения его структуры.

Каждый из пузырьков на диаграммах соответствует акциям соответствующих компаний. Диаметры пузырьков пропорциональны абсолютным значениям суммарной визуализируемой коррелированности котировок акций каждой из компаний по отношению к акциям остальных компаний, присутствующих в портфеле. Таким об разом, акции компании SIBN («Сибнефть») проявляют наибольшую общность в колебании своих курсов по отношению к акциям остальных компаний, а колебания курсов акций SBER («Сбербанка») ведут себя совершенно иначе по отношению ко всем остальным акциям портфеля. Пузырьки, расположенные по отношению друг к другу ближе чем шаг сетки, указывают на наличие корреляционной связи между котировками акций соответствующих компаний, и чем меньше это расстояние, тем пропорционально выше взаимосвязь. Таким образом, на диаграмме а можно визуально выделить две группировки компаний с положительно коррелированными курсами их акций: SIBN, LKOH, SNGS, TATN и SIBN, LKOH, YUKO - и коррелированную пару SIBN и AFLT; на диаграмме б представлены отрицательно коррелированные котировки акций компании RTKM с акциями компаний MSNG и EESR.

Таким образом, предложен новый вариант визуального представления структуры взаимосвязей между объектами статистической системы в виде пузырьковой

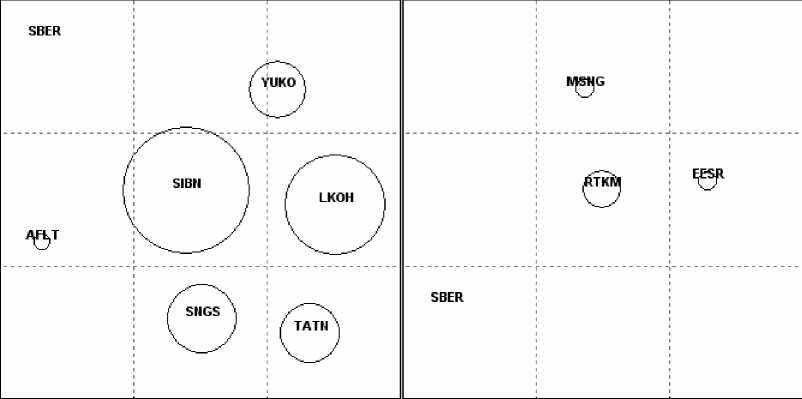
Диаграммы структуры корреляционных взаимосвязей котировок акций десяти известных компаний (см. таблицу): а - структура положительных связей; б - структура отрицательных связей

диаграммы структуры взаимосвязей, дано ее определение. Осуществлена постановка задачи по получению такой визуализации на основе модификации физической задачи N тел. В ходе решения задачи определены параметры диаграммы, построена математическая модель силового взаимодействия и разработан сходящийся алгоритм решения, отыскивающий стационарную точку системы.

Разработанный метод вносит свой вклад в семейство методов визуального отображения многомерных данных и может оказаться полезным инструментом для проведе ния разведочного анализа данных, особенно в тех случаях, когда задача исследования может быть сведена к определению и анализу структур взаимосвязей, задаваемых симметричными матрицами.