Применение формул Галкина для исследования эффекта смены знака коэффициента подъемной силы осесимметричных тел

Эффект изменения знака подъемной силы при изменении угла атаки в высокоскоростных плоских течениях впервые был обнаружен в [!]• в свободномолекулярном течении

такой эффект был найден в [2]. В работе [3] показано, что при обтекании клина разреженным газом при определенном соотношении угла полураствора и угла атаки подъемная сила клина может статв отрицательной. Причем этот эффект проявляется при любых скоростях газа и отношениях температур поверхности клина и газа. Более того, такой эффект есть и в случае гиперзвукового течения невязкого газа (модель Ньютона). Для высокоскоростных течений на основе локального метода [4] показано, что эффект изменения знака подъемной силы при определенных значениях угла полураствора существует для затупленных конических тел при произвольном числе Рейнольдса. Данная работа посвящена изучению этого эффекта для тел в форме степенных фигур вращения в гиперзвуковом потоке разреженного газа без предположения о режиме свободномолекулярного обтекания.

2.    Локальный метод

Для исследования эффекта смены знака подъемной силы в высокоскоростном потоке возможно использовать метод, основанный на гипотезе локальности [6,7], которая состоит в следующем: аэродинамические коэффициенты сил, действующие на элемент поверхности, зависят только от местного угла наклона Ө этого элемента к вектору скорости набегающего потока V_ro, от характерного для всего тела числа Рейнольдса Reo = роV^L/ро и температурного фактора Т_ш = Т_ш/То, где ро - коэффициент вязкости, вычисляемый по температуре торможения; То = Т^ [1 + S ²(у — 1)/у], Т_ш - температура торможения и температура элемента поверхности, соответственно; S = ^у/2М^ - скоростное отношение; М^ - число Маха набегатощего потока: у - отношение удельных теплоемкостей: L - характерный размер тела. В соответствии с гипотезой локальности предполагается, что для аэродинамических коэффициентов давления и трения (отнесенных к скоростному напору P^V/2 /2) справедливы соотношения [6,7]:

Ср = Ро sin² Ө + p1 sin Ө, С_т = то sin Ө cos Ө.                        (1)

Коэффициенты Ро,Р1,То являются функциями от числа Нео, температурного фактора Т_ш и показателя степени адиабаты у. Отличительной особенностью данной модели (кроме простоты) является то, что в предельных случаях изменения числа Рейнольдса она соответствует либо свободномолекулярной модели, либо модели Ньютона. Так, в свободномолекулярном случае (Reо ^ 0) [8]:

Ро = то = 2, pi =

^Тш

("г1 )•

а в случае невязкого высокоскоростного газа (Reо ^ то) имеет место формула Ньютона [9]:

Ро = 2, pi = 0, то = 0.

В промежуточной области коэффициенты ро,рі,то аппроксимируются следующими формулами [6,7] :

Ро = 2, pi =

У^ ( ^)

exp [—(0.125 + 0, 078tw)Reo] ,

то =

5.2326

Re + 6.88 exp(0.0072Re — 0.000016Re2)

Re = Reo [0.25 + 0.75tw]-2/3

3.    Квадратурные формулы Галкина

Для аэродинамических характеристик осесимметричного тела, обтекаемого под углом атаки а, существуют аналитические формулы в виде интегралов по продольной координате. Эти выражения были получены В. С. Галкиным и приведены в монографии [8], с. 360. Приведем эти формулы без вывода.

Пусть поверхность тела, обладающего цилиндрической симметрией, в прямоугольной системе координат Oхуz параметризована переменными х и у согласно формулам

( у = т(х) cos ), [ z = г(х) sin у,

где

0 < х <  L, 0 < у < 2 тг.

Функция т(х) предполагается дифференцируемой на всем отрезке [0, L], кроме, быть может, конечного числа точек, при этом будем полагать, что если у тела нет «затупления» при х = 0, то т(0) = 0, то есть «носик» тела находится в начале координат. Введем также функцию, зависящую от угла атаки а и от координаты х:

^ = Ш х

ctg а.

Тогда в этих обозначениях для коэффициента подъемной силы С_у (а) осесимметричного тела имеет место выражение в виде квадратуры:

^sin2a г

СУ(а) =--52~ къ 00

, / х Г/ X С(х)™а          , X X .

ФкДх) щ, - Та)            ₂ N⁽ДЛ^{х),а) +}

L        1 + ^(х) tg а

+Р1

V1 +  (х) tg² а

L(^Q,(х), а)

где функции N(z, а), L(z, а) имеют вид z2 tg2 а + 2 tg2 а — 1,           если z > 1,

N (z, а) = <

Г

[(z² tg² а + 2 tg² а — 1) arccos(—z) —

-^z Cl-Л ⁽3 - 2 tg^{2 а +} 322⁾] ,

если

|z| < 1,

0,

если z <  — 1.

L(z, а) = <

Г [(z² tg² а —

z² tg² а — 2 ,

2) arccos(—z) — zV 1 — z²

0,

( 2 ^— tg^{2 а}) ,

если z > 1, если |z| < 1, если z < — 1.

Для коэффициента силы сопротивления Сж (а) осесимметричного тела имеется выра жение

С$(а) = -^2 j йхт(х') |Д — Та)

£" (х) sin³ а

1 + €" (х) tg² а

F ⁽С^{(х)) +}

^" (х) sin² а                       л / х -            / хх

(Ю)

+Р1           х ^= ^с(^«^{(х)) + Т}а ^а^{(х)sin а}Н ⁽с^(х))

V1 + ^2 (х) tg2 а где функции F(z), G(z), Н(z) даются выражениями

	1 + 2І2,                         если г > 1,
F (г) = < Г	(1 + 2І2) arccos(—г) + 1 (Ц + |22) V1 — г2] , если |г| < 1,      (11) 0,                          если г < —1,

С(г) = <

1 + 212,

212) arccos(—г) + 23jv I

0,

г2] ,

если г > 1, если |г| < 1, если г < — 1,

Н (ж) = <

Г

1, a arccos(—г) + 1V1 — г² )

0,

если	г > 1,
если	|г| < 1,
если	г < —1.

4.    Тела вращения со степенной образующей

Рассмотрим тела вращения со степенной образующей. В этом случае образующая линия имеет вид

т(ж) = Ro (LУ , где 0 < ж < L, Ro - радиус основания тела, a L - его длина. Удлинением тела будем называть величину А = L/Rq, понятно, что тела с одинаковыми удлинением Л и степенью 3 подобны и при равных числах Рейнольдса и температурного фактора имеют одинаковые аэродинамические коэффициенты. Примеры образующих с удлинением Л = 1 для разных степеней 3 приведены на рис. 1. Схема обтекания тела потоком с углом атаки а приведена, на. рис. 2, а. примеры триангулированных тел вращения приведены на. рис. 3.

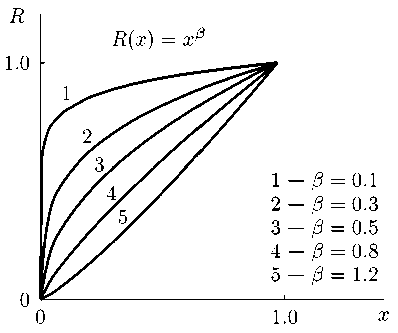
Рис. 1. Примеры образующих для степенных тел вращения

5.    Эффект Галкина. Критическое удлинение

Таким образом, рассматривается обтекание степенного тела вращения с удлинением Л и углом атаки 0 < а < я/2. Эффект Галкина состоит в том, что существует такое критическое значение удлинения Л_ст, что при Л <  Л_ст коэффициент подъемной силы тела Су (а) < 0 при 0 < а <л/2,а при Л >  Л_ст имеем Су (а) > 0 в некотором интервале значений угла атаки а из миожсства. 0 < а <  ^/2. На рис. 4 показан пример проведения фупкщш Су (а) при разных Л в окрестности Л_ст для степенного тела вращения.

Значение Лст для тела с заданной степенью образующей 3 и ПРИ заданных параметрах Re о и tw определяется с помощью следующей процедуры. Функция Су (а) вычисляется на отрезке 0 < а < атах в некотором количестве точек N по формуле (7) численным интегрированием методом Симпсона. После получения N значений функции Су (а) эта функция интерполируется сплайном. Используя этот сплайн, находится максимум этой функции на отрезке 0 < а < amax. Таким образом, получаем функцию Cmax(А). Численное исследование этой функции позволяет определить максимальное значение переменной А, при которой Cmax (А) < 0. Это максимальное значение и есть Аст, так как при А > Аст имеем Cmax(А) > 0. Проведенное исследование показало, что описанная процедура надежно определяет критическое значение Аст при amax = 10 град и при N = 5. С помощью описанной процедуры получены результаты, которые представлены на рис. 5 и 6.

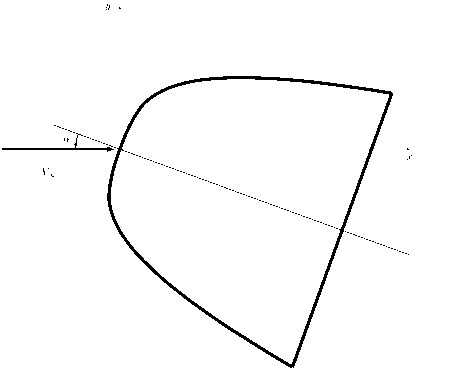
Рис. 2. Схема обтекания тела, а - угол атаки, V^ - скорость набегающего потока

а)

б)

в)

г)

Рис. 3. Примеры степенных тел вращения для Э = 0.1, 0.3, 0.5,1.1 соответственно

На рис. 5 представлена зависимость критического удлинения А_ст от степени образующей Э- Анализируя эти результаты, можно отметить не сильную зависимость А_ст от температурного фактора t_w. Кроме того, существует точка на графике с координатами Э = 0.21, А_ст = 0.89, в окрестности которой, проходят все линии зависимостей.

Чтобы подробно рассмотреть это явление, на рис. 6 представлены зависимости А_ст от числа Рейнольдса Re о при разных показателях степени Э ^в интервале 0.18 < Э <  0.26. На рис. 6 можно видеть некоторый кроссовер поведения функции А_ст (Reo) при разных Э она из возрастающей делается убывающей. Это происходит в окрестности Э ~ 0.21. При этом значении критическое удлинение степенного тела вращения почти не зависит от числа Re о.

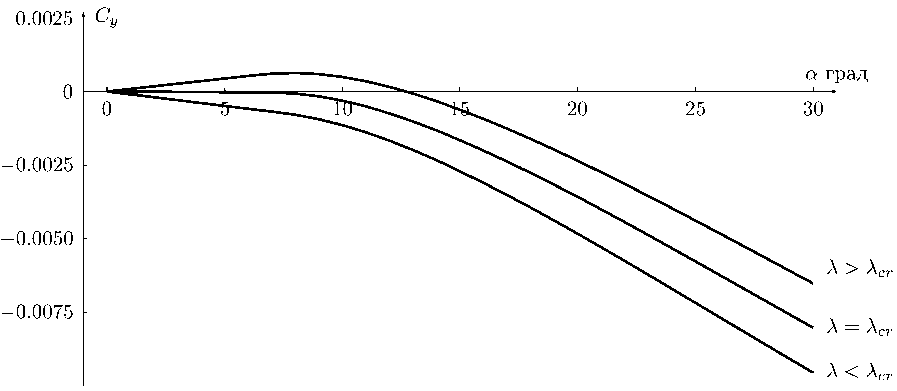
Рис. 4. Поведение коэффициента подъемной силы С_у при удлинениях тела вблизи критического. При А < А_ст коэффициент отрицателен при всех углах атаки

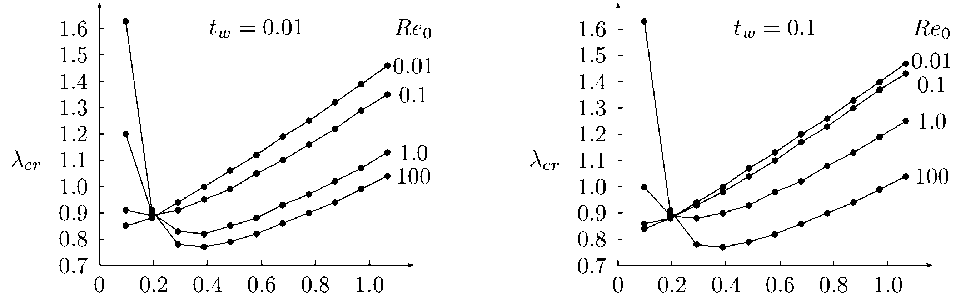
3                                    3

а)                                                     б)

Рис. 5. Критическое удлинение степенного тела вращения как функция степени 3 при разных числах Рейнольдса Reo и температурном факторе: а) ^w = 0.01, б) ^w = 0.1

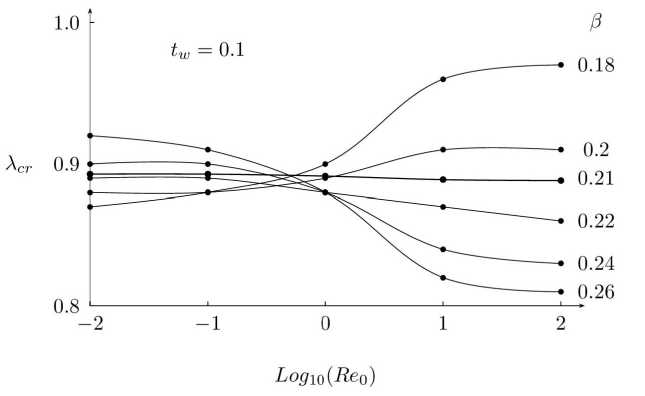
Рис. 6. Критическое удлинение степенного тела вращения как функция числа Re о при степенях 3, равных 0.18-0.26, и температурном факторе ^_w = 0.1

6.    Сравнение с суммированием по триангуляции

Таблица!

Критические удлинения степенного тела вращения для разных режимов обтекания

Показатель	Re о =	10 -4	Re о	=1	Re о	10 4
3	Хст (Т )	Хст (Q)	Хст (Т)	Хст (Q)	Хст (Т )	Хст (Q)
0.3	0.9474	0.9483	0.8826	0.8837	0.7868	0.7880
0.5	1.0750	1.0756	0.9385	0.9390	0.7922	0.7926
0.7	1.2071	1.2063	1.0317	1.0321	0.8625	0.8629
0.9	1.3433	1.3440	1.1403	1.1409	0.9509	0.9513
1.1	1.4845	1.4855	1.2598	1.2607	1.0506	1.0512

В табл. 1 приведены критические удлинения Х_ст (Т), вычисленные по триангуляциям, а также критические удлинения Х_ст (Q), вычисленные с помощью квадратуры по формуле (7). Как видно из таблицы, имеем хорошее совпадение результатов расчета обоими методами. Поскольку результаты, полученные двумя разными методами, отличаются меньше, чем на 0,01 % относительной ошибки, то это дает уверенность, что, во-первых, оба метода не содержат ошибок, а во-вторых, полученные результаты для критического удлинения являются надежными.

7.    Заключение

Для тел вращения со степенной образующей исследован эффект Галкина, который состоит в том, что существует критическое удлинение тела Х_ст, такое, что при всех Х <  Х_ст подъемная сила отрицательна при всех углах атаки а в интервале (0,тт/2). Исследована зависимость Х_ст от степени образующей 3; числа Рейнольдса Reo и температурного фактора t_w. Обнаружено явление кроссовера в поведения функции Х_ст (Reo), при 3с ~ 0.21, так что при 3 > 3с эта функция возрастающая, а при 3 < 3с убывающая. Соответственно при 3 = 3с критическое удлинение не зависит от числа Рейнольдса.