Применение функции качества, зависящей от массы, при исследовании усреднительных систем

Одним из важных показателей качества горной продукции является постоянство ее характеристик, требуемый уровень которого достигается усреднением продукции в специальных системах. Теоретические экспериментальные исследования усреднительной системы осуществляют с помощью функции качества, в роли которой выступает какая-либо характеристика горной продукции, важная с практической точки зрения.

Об эффективности усреднительной системы судят по изменению функции качества в результате усреднения горной продукции. Одним из распространенных количественных показателей степени усреднения является его коэффициент

ξ = σвх (1) σ вых где σвх и σвых – средние квадратические отклонения функции качества на входе в систему и выходе из нее [1]. Коэффициент ξ показывает, во сколько раз уменьшилась средняя амплитуда колебаний функции качества. Несмотря на важность такой характеристики усреднения, она не является полной, так как нельзя в одном числе охватить все изменения, происшедшие с функцией. Для полного анализа всех изменений функции качества применяют функцию корреляции, ее спектр, а также спектр самой функции качества. В данной статье автор использует спектр функции качества.

Функция качества непосредственно связана с горной продукцией, поэтому аргументом этой функции должна быть физическая величина, которой измеряют горную продукцию. Как правило, такой величиной является масса, поэтому она является естественным аргументом функции качества. Однако во всех исследованиях применяется функция качества, зависящая от времени, но это не совсем удобно.

Использование функции качества, зависящей от времени, требует измерения горной продукции в единицах времени. Это можно осуществить при прохождении продукции в потоке через некоторую точку пространства, в которой измеряется функция качества. В этом случае необходима дополнительная информация о производительности потока, поскольку функция качества, зависящая от времени, без данных о производительности потока содержит не всю информацию о качестве продукции. Поясним это на примере.

Пусть два потока горной продукции имеют одинаковые функции качества, однако производительность первого во много раз больше производительности второго. Если колебания функции качества выходят за допустимые пределы, то в первом случае потребуются специальные мероприятия по усреднению продукции, а во втором случае с усреднением справится другое оборудование, осуществляющее дробление горной продукции, ее перегрузку и т. п. и имеющее сравнительно небольшие размеры рабочих емкостей. Следовательно, знания зависящей только от времени функции качества недостаточно для принятия правильных мер по усреднению.

В математическую модель усреднительной системы, построенную с помощью зависящей от времени функции качества, всегда входит производительность потока горной продукции. Однако эта информация не связана с усреднительной системой, и ее попадание в модель говорит о несовершенстве этой модели.

Функция качества, зависящая от массы, не имеет перечисленных недостатков. Она содержит полную информацию о показателе качества горной продукции. Модели усреднительных систем, построенные с ее помощью, зависят только от параметров этих систем, компактны, информативны и удобны для анализа.

Рассмотрим применение зависящей от массы функции качества на примере построения математической модели усреднительного штабеля. Исследованию усреднительных штабелей и сходных с ними систем бункерного усреднения посвящено много исследований (см., например, [2–5]), поэтому есть возможность сравнить представленную ниже модель с известными. Однако для большей убедительности рассмотрим такой ус-реднительный штабель, исследование которого нельзя считать исчерпывающим.

Речь идет о самом простом усреднительном штабеле, параллельные слои которого формируются в одном направлении. Такая же схема усреднения реализуется в многоячейковом бункере с поочередной вертикальной загрузкой ячеек и их одновременной нижней разгрузкой на общий конвейер, где и происходит смешивание (рис. 1). В работах [2; 3], где данная схема рассматривается, исследование заканчивается формулой дисперсии функции качества усредненной продукции. Это позволяет оценить степень усреднения с помощью формулы (1) или подобных ей. Однако при этом отсутствует амплитудно частотная характеристика усреднения и подробный анализ функции качества на выходе из системы, в то время как для других систем усреднения это проделано. Восполним этот пробел, применяя функцию качества, зависящую от массы (рис. 1).

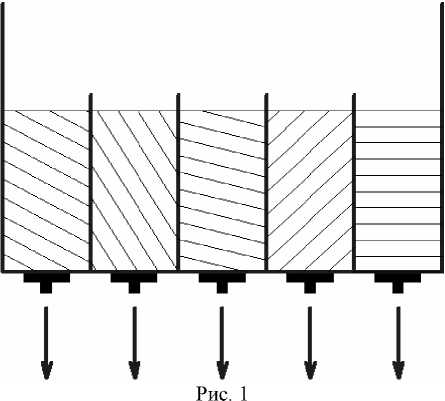
Обозначим через K 1 ( m ) и K ₂( m ) функции качества до и после усреднения соответственно, где m - масса горной продукции. Пусть M - масса штабеля, а массы слоев штабеля одинаковы и равны M 0 . Тогда число слоев n = M / M о . В соответствии со схемой усреднения функция качества K 2 ( m ) задана формулой

1 n ^{- 1} ( m ^

K ₂( m ) = S K J— + iM ₀ 1 , 0 <  m <  M . (2) n i = 0 I n )

Запишем преобразование Фурье (спектр) исходной функции качества в виде

+to

F ( K 1 ( m )) = F ( m ) = J K 1 ( m ) e ^{- 2 п j m m}dm ,    (3)

-to где j - мнимая единица. Функция K 1(m) восстанавливается с помощью обратного преобразования Фурье:

+to

K 1 ( m ) = J F 1 { m ) e ^{2 n} j ^m m d _ю .        (4)

-to

Аналогично получим, что F ( K ₂( m )) = F ₂(и) -прямое преобразование Фурье функции К ₂( m ), а

+to

K ₂( m ) = J F ₂{ m ) e^{2 n j m m}d m           (5)

-to

- обратное преобразование Фурье этой функции. Подставим (4) в (2):

1 n - 1 ^+to          2 п j m ( m + iM ₀)

K2(m) = SJ F1(m)e   n n i=0-to после преобразований получим

+to

K2(m) = J F1(m)a(m)e    ndm,(6)

-to n-1

a(m) =1S e jmM0i .(7)

n i = 0

Подстановка x = и/ n позволит записать формулу (6) в виде

K2(m) = pF(nx)a(nx)e2njxmdx .(8)

-to

Сравнивая (8) и (5) и учитывая, что обозначение переменной интегрирования не влияет на результат, представим связь между спектрами функции качества до и после усреднения в виде

F ₂ ( m ) = nF 1 ( n m ) a ( n m ).         (9)

Связь (9) не является простой, и теперь понятно, почему амплитудно-частотная характеристика усреднения еще не получена. Однако эта связь вполне поддается анализу.

Пусть

F ₀( m ) = F 1 ( m ) a ( m )          (10)

есть спектр некоторой функции K ₀( m ). Тогда, пользуясь свойствами спектра, по формуле (9) получим

F 2 ( m ) = nF 0 ( n m ) = F ( K e ( -)).       (11)

n

По уравнению (11) следует K ₂( m ) = K ₀( m / n ), т. е. K ₂( m ) является растянутой в n раз функцией K ₀( m ), и поэтому дисперсии этих функций равны.

Итак, спектр F 1 (и) переходит в спектр F ₂(и) в результате двух операций: умножения (10) на функцию а(и) и сжатия (11) полученного произведения в n раз. При этом уменьшение колебаний функции качества происходит только в результате первой из них. Сжатие не меняет размаха колебаний, однако оно тоже играет важную роль, о которой будет сказано ниже.

Исследуя уменьшение колебаний качества найдем более удобную формулу для функции а(и). Умножение формулы (7) на exp(2n j и M ₀) дает

a ( m ) e ^{2п j m M 0} = ¹ j^ e ^{2n j m M 0} i .         (12)

n i = 1

По формулам (7) и (12) находим

a(m)e2njmM0 - a(m) = 1(e2njnM0 -1), n откуда, с учетом nM0 = M выразим а(и):

a(m) = e ™j ™( m - m 0) _sin(nmM)_ n • sin(nmM 0)

Тогда sin(ntoM) а(ю) =               .           (13)

n • |sin( пю M ₀

На основании формул (10) и (13) получим связь между амплитудными спектрами:

।=м (14) n ■ |sin( nm M ₀

Функция (13) практически совпадает с известной амплитудно-частотной характеристикой другой усреднительной системы - многоячейкового бункера, размеры n ячеек которого зависят от номера ячейки V i = A i , i = 1, 2, _, n , загрузка производится тонкими горизонтал ьными слоями, а разгрузка - одновременно из всех ячеек на общий конвейер [2; 5]. Отличие заключается только в константах: амплитудно-частотная характеристика в [2] зависит от объема A первой ячейки, объема всего усреднительного бункера и производительности потока горной продукции, а функция (13) - только от M и M ₀. Совпадение функций говорит об одном усреднительном механизме сравниваемых систем, однако различие в константах является принципиальным: функция (13) зависит только от параметров усреднительной системы, а амплитудно-частотная характеристика в [2] - еще и от производительности потока.

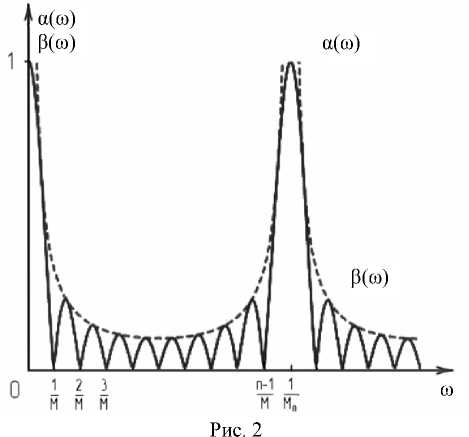
Функция (13) имеет период 1/ M ₀, поэтому достаточно рассмотреть ее на отрезке 0 < и < 1/ M ₀. Она равна 1 при и = 0 и и = 1/ M ₀, а во внутренних точках рассматриваемого отрезка справедливы неравенства |а(и) |< 1 и |sin (пи M ₀)| > 0. Следовательно, на интервале 0 < и < 1/ M 0 функцию |а(и)| можно рассматривать как периодическую функцию |sin (пи M )|, умноженную на свою огибающую в(и) = 1/( n |sin(пи M )|). Огибающая в(и) имеет наименьшее значение 1/ n в середине интервала, медленно растет к его границам и только вблизи этих границ растет круто. Кроме того, функция |sin(пи M )| принимает нулевые значения в точках и = 1/ M , 2/ M , ..., ( n - 1)/ M = 1/ M 0 - 1/M.

График функции |а(и)| при n = 10 (рис. 2) показывает, что интенсивное уменьшение амплитуды колебаний происходит на отрезке частот 1/M < и < 1/M0 - 1/M, а с учетом периодичности функции |а(и)| - на отрезках r 1 , r +1    1

--1--<ю<--- , r = 0, ± 1, ± 2,.... (15)

M ₀ M M ₀ M

На остальных частотах г 1

ю-- < — , r = 0, ± 1, ± 2,...       (16)

M0 M происходит лишь незначительное уменьшение амплитуды и энергии колебаний.

Энергию колебаний можно определить в частотной области как интеграл от энергетического спектра [6]. Тогда по формулам (13), (14) следует

+/

D ( K 2 ) = D ( K 0 ) = — /а ( ®)| • F 1 ( ®)| d ю , (17)

M -/ где D(K) - дисперсия функции K(m). Поэтому конечный результат зависит не только от функции |а(и)|, т. е. от усреднительной системы, но и от амплитудного спектра |F 1(и)| исходной функции качества.

Спектр | F 1 (и)| определен на всей бесконечной оси частот, однако его основная энергия сосредоточена на интервале частот конечной длины. Если этот интервал включает много периодов функции |а(и)|, т. е. является широким, и в пределах одного периода спектр | F 1 (и)| меняется мало, то, учитывая периодичность функции |а(и)|, формулу (17) можно заменить формулой

1/

M/ M °,     ,2      +/      .2

D ( К ₂) = ⁰ j а ( ю ) d ю- j F ( ю ) d ю .

M ,          -/

Тогда коэффициент усреднения

5 =

( DK ) У

I D ( K 2 ) J

V м 0

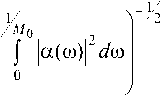
= ^ (18)

зависит только от n . Выражение (18) является предельной оценкой коэффициента усреднения при M ^ да и зависит только от числа слоев ус-реднительного штабеля.

Фактический коэффициент усреднения может значительно отличаться от предельной оценки (18), особенно в случае узкого спектра |F 1(и)|. Если такой спектр принадлежит одному из интервалов (15) (как правило, первому, т. е. при r = 0), то коэффициент усреднения более чем в два раза превосходит оценку (18). Если же один из интер- валов (16) захватывает бόльшую часть спектра, то коэффициент усреднения близок к 1, т. е. в этом случае произойдет лишь незначительное уменьшение энергии колебаний. Практически не ослабляются низкочастотные колебания, частота которых принадлежит первому (r = 0) интервалу (16), а период больше массы M усреднительного штабеля (см. рис. 2).

Следовательно, эффективность усреднения можно повысить, если настраивать усреднитель-ный штабель на конкретную функцию качества, а не применять его вслепую. Проделанный анализ показывает, что для этого необходимо знать отрезок частот

^Ю н <  ^Ю <  И в ,              (1⁹⁾

на который приходится основная энергия спектра исходной функции качества, и выбрать параметры усреднительного штабеля по формулам

M = —, M 0 =-- ¹---,      (20)

Юн        Юн + Юв чтобы отрезок (19) совпал с первым (r = 0) отрезком (15).

Вернемся к эффекту сжатия спектра. Если параметры штабеля выбираются по формулам (19), (20), то учитывая сжатие спектра в n раз в результате усреднения, в нем практически отсутствуют высокочастотные колебания. Это особенно важно учитывать, когда усреднительный штабель является частью усреднительных мероприятий. В частности, оборудование усреднительного или другого назначения с рабочими емкостями относительно малого объема желательно применять до усреднительного штабеля, так как его применение после штабеля не приводит к уменьшению колебаний функции качества. Отметим еще одно следствие сжатия спектра: повторное усреднение горной продукции в таком же усреднительном штабеле вновь приводит к значительному уменьшению энергии колебаний. Для сравнения: упо- мянутый выше усреднительный бункер с горизонтальной загрузкой ячеек тонкими слоями не обладает эффектом сжатия спектра, и его повторное применение не приводит к заметному уменьшению энергии колебаний.

Итак, построение математической модели ус-реднительного штабеля с использованием зависящей от массы функции качества показало, что на результат усреднения оказывают влияние только функция качества и два параметра штабеля: его масса и масса одного его слоя. Это позволило детально изучить механизм усреднения штабеля, оценить коэффициент усреднения и получить его предельную оценку, обнаружить эффект сжатия спектра, дать формулы по расчету параметров штабеля для достижения наилучшего усреднения и рекомендации по выбору оптимального места штабеля в ряду других усреднитель-ных мероприятий.