Применение функций Крылова А. Н. для решения задач строительной механики

Статья посвящена вопросу применения аналитических и численных методов в задачах расчета сооружений. В настоящее время большинство задач строительной механики решается методом конечных элементов (МКЭ) [1, 6, 14, 20, 25, 27, 28]. Разработано огромное количество элементов для решения различных задач механики. Применяемые в элементах аппроксимации отвечают лишь общим принципам механики сплошных сред. Компоненты матриц жесткости элементов определяются численным интегрированием. Это вносит определенные погрешности в решение. С другой стороны, в строительной механике аналитически решено большое количество задач. В данной статье предлагается вариант улучшения конечно-элементного решения за счет использования аналитического решения при построении матрицы жесткости. Предложен конечный элемент для решения задачи изгиба балки на основании Винклера [13]. Функция прогибов определяется решением Крылова А. Н. [13, 30]. Интегрирование при построении матрицы жесткости выполняется точно. Подчеркивая актуальность применения аналитических решений, в статье показывается, как то же решение Крылова А. Н. используется для анализа численного расчета круговой цилиндрической оболочки [3, 12].

2.    Обзор литературы

Развитие метода конечных элементов как численного метода решения задач расчета сооружений идет по пути усложнения применяемых математических моделей [2, 4 ,7 - 9, 11, 15, 16, 23, 26, 29]. Этот метод реализован во многих промышленных программных комплексах, таких как: SCAD, ANSYS, NASTRAN, PLAXIS, SOFiSTiK, ЛИРА [5, 10, 21]. Используемые в комплексах конечные элементы строятся на базе приближенной аппроксимации неизвестной функции в пределах элемента, что приводит к погрешностям решения. В данной статье рассматривается другой, более эффективный подход к построению конечного элемента, когда вид искомой функции в пределах элемента определяется точным решением дифференциального уравнения задачи, а погрешность возникает только при решении системы уравнений равновесия для всей расчетной области.

Предлагаемое использование аналитического решения в реализации процедуры метода конечных элементов отсутствует в литературных источниках. Актуальность данной работы вызвана стремлением совершенствовать процедуру МКЭ путем приближения конечно-элементной модели к реальной работе сооружения.

3.    Постановка задачи

Задачами настоящей статьи являются:

• 1.    разработка конечного элемента на базе аналитического решения дифференциального уравнения, определяемого функциями Крылова А. Н.;

• 2.    решение задачи изгиба балки на основании Винклера методом конечных элементов с применением созданного элемента;

• 3.    исследование "краевого эффекта" в осесимметричной задаче изгиба цилиндрической оболочки на базе функций Крылова А. Н.

4.    Функции Крылова А.Н.

Рассмотрим однородное дифференциальное уравнение:

d ⁴ w

B ⁰ +kw =0 dx ^{4        0}

Аналитическое решение этого уравнения имеет вид [13, 30]:

w 0 (x) = C 0 V o ('x ) + C V (' x ) + C 2 V 2 (ex ) + C 3 V 3 ('x )

Здесь:

• ^P = ^ 4B , ■■■ C0 , C 1 , C 2 , C³ " – неопределенные коэффициенты,

V_i(βx) – функции Крылова А. Н., определяемые соотношениями:

e ''x I e 'x

V _o ('x) = ch 'x • cos 'x =-- cos 'x

,- 'x

. . .       .       1 , .                                                            1 (e'11 + e e'x - e 'x

• sin 'x +           • cos 'x

V/ 'x) = —( ch 'x • sin 'x + sh 'x • cos 'x ) = 2 '                                 2 ' I 2

1                         1 e ' ^x _— e ' ^x

V₂( 'x) = —shh 'x • sin 'x = —₇--sin 'x

²          2 ' ²                   2 ' ²      2

1                                         1 Г в^вх + e ^в

V 3 (вх) = 4 ^ 4 ( ch вх ■ sin вх - sh вх ■ cos вх ) = 4^ 1---- 2---

■ sin вх -

e ^ ¹ - e - ^вх

--cos Вх

Далее покажем, как используется решение (2) для исследования таких различных задач строительной механики как изгиб балки на основание Винклера и осесимметричный изгиб круговой цилиндрической оболочки. При этом задачи будем решать и аналитически, и численно методом конечных элементов.

5.    Изгиб балки на упругом основании

Обратимся к уравнению изгиба балки на основании Винклера [13, 19, 30]:

d ⁴ w

EJ + Kw = q(x)                                          ₍₇)

dx ⁴                                                                           ( )

Здесь w(x) – функция прогибов балки, EJ – изгибная жесткость балки, K – коэффициент жесткости основания, q(x) – действующая на балку внешняя нагрузка.

Общее решение этого уравнения складывается из решения w ₀ (x) соответствующего однородного уравнения:

d ⁴ w

^EJ__ 4 ₊ ^KW = 0

и частного решения w ₁ (x) , определяемого заданной нагрузкой q(x) [30]:

w(x) = w 0 (х) + w 1 (х)

Однородное уравнение (8) совпадает с уравнением (1) при B = EJ и k=K следовательно, w ₀ (х)

определяются зависимостью (2), где в =

K

N 4 ■ EJ

. Получение частного решения w ₁ (x) при произвольной

нагрузке на балку весьма сложно.

Как отмечалось, в настоящее время основным методом решения задач строительной механики является метод конечных элементов [6, 17, 18, 23, 26]. При этом для аппроксимации неизвестной функции на элементе обычно используются линейная, квадратичная или кубическая функции [14, 25]. Для решения задачи изгиба балки на винклеровском основании в данной работе построен элемент на базе точного решения (2) уравнения изгиба в пределах элемента. Такой элемент имеет два узла с двумя степенями свободы в каждом: прогибом и углом поворота (рис.1). Вектор узловых перемещений элемента [25]:

U

элемента

w_i w‘ w j ^w ‘

□------------□

Рис. 1. Конечный элемент балки

Матрица жесткости элемента строится методом, применяемым в строительной механике [15, 27, 29]. Подход основан на том, что если закрепить от возможных перемещений оба узла элемента, а затем последовательно полагать одну из компонент вектора узловых перемещений равной единице и определять усилия в узлах элемента, то эти усилия составят столбцы матрицы жесткости элемента. Во всех рассматриваемых вариантах перемещения точек элемента w(x) определяются зависимостью (2). Неопределенные коэффициенты в решении (2) находятся из четырех вариантов граничных условий, представленных в таблице 1:

Таблица 1

Вариант	Узел i ( x = 0 )		Узел j ( x = L )
	w	w ‘	W	w ‘
1	1	0	0	0
2	0	1	0	0
3	0	0	1	0
4	0	0	0	1

Полученная в каждом случае функция w(x) точно описывает перемещения точек элемента. Следовательно, определенные по ней узловые усилия, являющиеся компонентами матрицы жесткости, точно удовлетворяют уравнениям равновесия элемента. Полученная матрица жесткости элемента имеет вид:

EJ

A

4 в VV + V 0 V 1 V 1 ²

V 1 V 2 симметрично

—

V 2 V 0

—

V 0 V 3

V 1

V 2

4 в 4 VV + VV

V 2

V 3

V 2 V 0 — V ²

V 1 V 2

—

V 0 V 3 J

,

где A = V ₂ ² — VV 3 . Аргументом всех функций является eL .

Кроме построения матрицы жесткости для использования элемента необходимо построить вектор узловых усилий, обусловленных распределенными нагрузками, действующими на элемент. Рассмотрим случай только равномерно-распределенной нагрузки. Для приведения ее к эквивалентным узловым усилиям [6, 14] решается задача изгиба защемленной в узлах балки при действии равномерно распределенной нагрузки. Общее решение уравнения изгиба в этом случае имеет вид [30]:

w(x) = w 0 (x) + w 1 (x) = w 0 (x) + q ,

K где q - частное решение, соответствующее нагрузке q; w (x) определяется зависимостью (2), в K0

которой коэффициенты вычисляются из граничных условий:

x = 0 w = 0 ,w ' = 0 ; x = Lw = 0 ,w ‘ = 0 ; .

Используя известные зависимости [25] для определения усилий в балке:

d3wd

Q(x) = — EJ    , M(x) = — EJ, dx3

получаем следующие выражения для усилий в узлах:

P 2 i = — P 2 j = EJ^ ( V o V 2 + 4 в⁴V 2 ) , K A

P 1 i = P 1 j = EJ-q- ( V o V — V 1² + 4 в⁴V a V 2 ) ,

K A

6.    Пример расчета балки на основании Винклера

С использованием разработанного элемента были решены задачи изгиба балки длиной 30 м, жесткостью на изгиб EJ = 1 ■ 10 6 кн * м², опирающейся на основание Винклера с коэффициентом жесткости K = 400 кн/м³ . По длине балка разбита на три конечных элемента. Рассмотрены два варианта нагружения:

• 1)    сосредоточенная сила P = 100 кН на правом конце,

• 2)    сосредоточенный момент М = 200кНм на правом конце.

Полученные в результате расчетов значения прогибов (мм) приведены в Таблице 2, где они сравниваются с точным решением (2) уравнения (7) при соответствующих граничных условиях и решением той же задачи МКЭ с кубической аппроксимацией на элементе [20].

Таблица 2

	Вариант нагружения
	1			2
Х (м)	Точное решени е	Решение МКЭ		Точное решени е	Решение МКЭ
		Новый элемент	Элемент с кубической аппроксим.		Новый элемент	Элемент с кубической аппроксим.
0	-0,5650	-0,5650	-0,5591	-0,2818	-0,2818	-0,2716
10	-3,349	-3,349	-3,345	-1,8722	-1,8722	-1,8646
20	10,193	10,193	10,112	-1,1777	-1,1777	-1,1799
30	50,328	50,328	50,152	-10,004	-10,004	-9,9864

Результаты демонстрируют эффективность построенного конечного элемента, так как даже на сетке из трех элементов достигается точное решение задачи, а численное решение с кубической аппроксимацией на элементе имеет определенную погрешность. Из таблицы видно, что при действии на край балки сосредоточенной силы или момента наблюдается быстрое затухание перемещений от точки приложения усилия, что свойственно решениям, построенным на базе функций Крылова А. Н.

Особенно важно это свойство функций Крылова А. Н. для описания явления «краевого эффекта» в оболочках, когда в небольшой области тела наблюдается резкое изменение перемещений и усилий, которое плохо моделируется численными методами.

Исследуем «краевой эффект» на примере круговой цилиндрической оболочки при осесимметричном нагружении. Рассмотрим напряженно-деформированное состояние резервуара, находящегося под действием внутреннего постоянного давления. Он образован цилиндрической оболочкой [3, 22] постоянной толщины, защемленной по нижней границе (рис. 2)

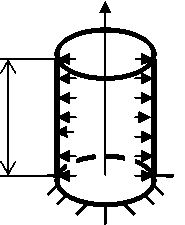
Рис. 2. Цилиндрическая оболочка под действием постоянного давления

Отметим, что в случае действия осесимметричной нагрузки неизвестные усилия, деформации и перемещения в цилиндрической оболочке не зависят от полярного угла. Это приводит к упрощению системы уравнений равновесия оболочки [12, 22], которая с учетом только внутреннего давления q cводится к неоднородному линейному обыкновенному порядка с постоянными коэффициентами:

d4w Eh d     + "etw = q, dx4 R2

дифференциальному уравнению четвертого

где w – перемещение вдоль радиуса оболочки,

Eh3

D = —7--- 12 ( 1 - v² )

–

цилиндрическая жесткость

оболочки, h – толщина оболочки, R – радиус оболочки, материала оболочки, v - коэффициент Пуассона.

Общее решение этого уравнения складывается уравнения w0 и частного решения w1 :

q – внешняя нагрузка, Е – модуль упругости

из решения соответствующего однородного

w = w₀ + w 1 ,

В качестве частного решения может быть принят прогиб, полученный по безмоментной теории [12]:

qR² ( 1 - v² ) w. =-----------

1 Eh

Далее ищем решение однородного уравнения:

d⁴w   Eh

^D-dw ° ⁺ Rew- = ⁰ .

Очевидно, что данное уравнение аналогично уравнению (1). Введем обозначение

₄₆ . = Eh = 12 ( 1 2 ^ 2) R²D    R²h²

.

Тогда исследуемое уравнение примет вид:

dw + 4 p⁴w₀ = 0 .

dx^{4          0}

Решение однородного уравнения (13) в случае расчета оболочек удобно записать в форме, построенной на базе функций Крылова А. Н. (3)–(6), но несколько отличной от вида решения (2) [3, 22]:

w₀ = e ^ ^x ( C 1 cos px + C 2 sin px ) + e ^{e x} ( C 3 cos px + C 4 sin px )

Отметим, что функция w 0 состоит их двух частей: первой с коэффициентом e ^{e x} , быстро

убывающей по мере удаления от края x = L , и второй с коэффициентом e

^{e x} , быстро убывающей по мере

удаления от края x = 0 . При достаточной длине оболочки обе части выражения для прогиба имеют самостоятельное значение. Общее решение исходного неоднородного уравнения (9) принимает вид:

w = e^ex ( C 1 cos px + C 2 sin px ) + e

qR² ( 1 - v² )

^ex ( C 3 cos px + C₄ sin px ) +---- Rh"

Константы интегрирования С1, С2, С3, С4определяются из четырех граничных условий. Причем на каждом крае (торце) цилиндра могут быть поставлены по два граничных условия [3,12]:

x = 0: w = 0, — = 0 dx x = L: M, = -Ddw = 0, Q, = -Ddw = 0 1dx21dx3

Как отмечалось выше, прогиб оболочки представляет собой по форме две пары быстро затухающих периодических функций. Каждая пара затухает по мере удаления от верхнего или нижнего края.

Используя это свойство решения при записи граничных условий в длинной цилиндрической оболочке (высота > 2в) в выражении для w нужно брать лишь одну часть общего решения, соответствующую рассматриваемому краю.

Таким образом, при постановке граничных условий для каждого края достаточно длинной цилиндрической оболочки, получим по два независимых алгебраических уравнения для определения лишь двух произвольных постоянных вместо системы четырех уравнений с четырьмя неизвестными в общем случае, когда влиянием краев друг на друга пренебречь нельзя.

Рассмотрим расчет резервуара со следующими параметрами:

n= 0.2 E=2*107 кН/м2 h= 0.12м, L=4м, R=2м

п

Резервуар находится под внутренним давлением q = 20кН/м2, параметр ^= 1.1814, т.е. высота резервуара L >2в . Следовательно, в выражении для прогиба используем одну ветку из выражения (14) для функции w0 (x) , описывающую перемещения, затухающие к верхнему краю, где усилия равны нулю:

w = e ^e x ( C 3 cos px + C₄ sin px ) +

qR² ( 1 - v² )

Eh

Параметр в , согласно (12), равен:

в =

3- ( 1 - v² ) E-h

2.6592 .

Произвольные постоянные С3иС4 определим из граничных условий на защемленном крае:

x = 0: w = 0, — = 0 ^ C = C = - 3.2 - 10-⁵ . dx     ³⁴

Следовательно, прогиб, соответствующий решению однородного уравнения представляет собой быстро затухающую при удалении от нижнего края периодическую функцию:

w₀(x) = e - ^26592x ( C₃ cos2.6592x + C₄ sin2.6592x ) = - 3.2 - 10 - ⁵e - ^26592x ( cos(2.6592 x) + sin(2.659

Графики функций w ₀ (x) и w(x) изображены на следующем рисунке:

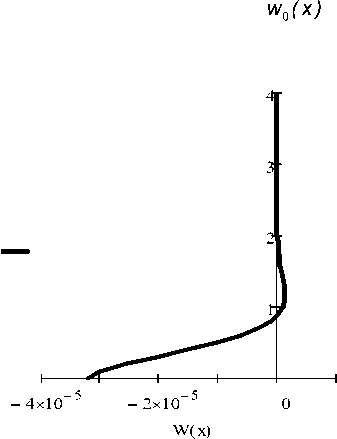
w(x) = w 0 (x) + w 1

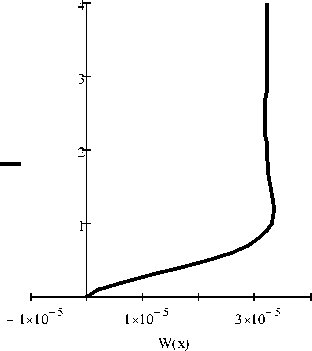
Рис. 3. Прогибы оболочки, соответствующие решению однородного и неоднородного уравнений

Внутренние усилия в оболочке при заданной формулой (18) функции w(x) определяются выражениями (17), откуда получаем:

M (x) = 2 • C 4 D p² e - ^ex ( cos px - sin px )

Q(x) = -2 • Dp³e ^{- ex} [ ( C₃ + C₄ ) • cos px + ( - C₃ + C₄ ) • sin px ]

Графики M(x) (кНм) и Q(x) (кН) представлены на рисунке 4:

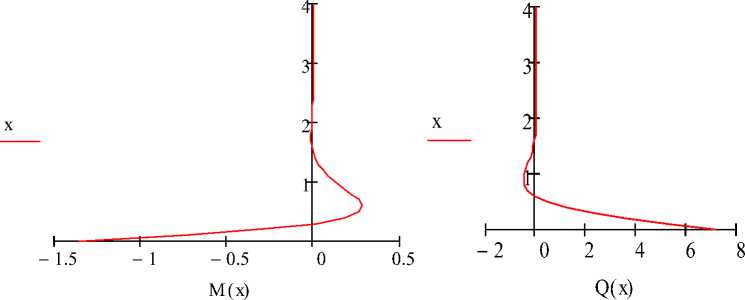
Рис. 4. Внутренние усилия по высоте оболочки

Кольцевое усилие N2 изменяется следующим образом [12,22]:

N 2 (x) = [ - 3.2 • 10 ^- 5 e ^{- 2} .6 ^592x ( cos(2.6592 x) + sin(2.6592x) ) +

20 • R² • ( l - v² )

E • h

] •

E • h

R • ( I - v² )

Графики изменения усилий N 2 (x) ( kH ) и N(x) ( kH ) :

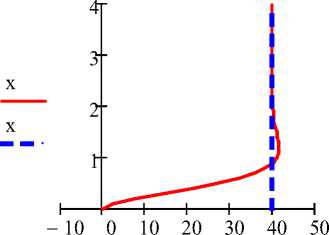
N2(x) , N(x)

Рис.5. Кольцевые усилия по высоте оболочки

Обозначенная пунктиром эпюра N(x) = 40 , соответствующая расчету по безмоментной теории [3, 12, 22], отличается от решения по моментной теории (сплошная линия) только у заделки. Здесь нагрузка воспринимается, в основном, за счет возникновения моментов и поперечных сил.

Таким образом, усилия в оболочке рассматриваемого резервуара в области, удаленной от защемления могут быть определены по безмоментной теории [12, 22]. В области же, примыкающей к заделке, возникают краевые усилия М(х) и Q(x) изгибного состояния которые влияют на перераспределение усилий безмоментного состояния оболочки. Поведение функций М(х) и Q(x) определяется с помощью функций Крылова А. Н.

Наблюдаемое на эпюрах быстро затухающее напряженно-деформированное состояние оболочки, обусловленное ее изгибом вблизи защемления, называется «краевым эффектом» [3, 12, 22]. Такие резкие изменения усилий плохо моделируются МКЭ [6, 27].

Сравним, например, аналитическое и численное решения для функции моментов в области 0 < x м 0.7 :

Таблица 3

X(м)	M (аналитическое решение)	M (решение SCAD, шаг сетки 0,1м)
0	-1.36	-1.07
0.1	-0.73	-0.5
0.2	-0.28	-0.13
0.3	0.01	0.11
0.4	0.18	0.24
0.5	0.26	0.29
0.6	0.31	0.29
0.7	0.26	0.25

Как видно из таблицы погрешность численного решения при x = 0 составляет 30%, причем в сторону уменьшения усилия. Численное решение методом конечных элементов всегда сглаживает сложное поведение искомой функции, и для получения ее экстремальных значений нужно проводить серию расчетов с уменьшаемым шагом сетки.

7.    Заключение

Полученные выше результаты позволяют сделать следующие выводы:

• 1.    На базе аналитического решения дифференциального уравнения, определяемого функциями Крылова А. Н., предложен новый конечный элемент. Матрица жесткости элемента вычислена точно и не имеет обычной погрешности МКЭ, связанной с приближенной аппроксимацией неизвестной функции и с численным интегрированием в пределах элемента.

• 2.    Конечноэлементное решение задачи изгиба балки на основании Винклера продемонстрировало эффективность разработанного элемента по сравнению с традиционным элементом с кубической аппроксимацией. Численное решение на базе нового элемента совпадает с точным решением задачи.

• 3.    Исследование "краевого эффекта" в осесимметричной задаче изгиба цилиндрической оболочки на базе функций Крылова А. Н. показало, что зоны быстрого изменения усилий плохо моделируются методом конечных элементов.