Применение генетических алгоритмов для оптимизации бизнес-процессов

Повышение качества управления бизнес-про-цессами в сложных социально-экономических системах уже долгое время остается актуальной задачей и имеет важное научное и практическое значение. Для уменьшения рисков при оценке эффективности управляющих воздействий применяются новые информационные технологии, в частности, имитационное моделирование. Однако зачастую даже при наличии имитационной модели бизнес-процесса определить, какие из возможных вариантов управляющих взаимодействий приведут к желаемой цели, бывает довольно сложно. В таких случаях вместо того, чтобы перебирать все возможные варианты вручную, целесообразно воспользоваться одним из алгоритмов поиска оптимальных или квазиоптималь-ных решений.

В этих условиях актуальным видится вопрос адаптации существующих методов поиска оптимальных решений для решения задач оптимизации бизнес-процессов.

Генетические алгоритмы

Одной из основных задач управления является оптимальное использование ресурсов и времени. Таким образом, задача оптимизации связана с понятием целевой функции, представляющей собой математическое выражение некоторого критерия качества исследуемого процесса, экстремум которой нужно найти. Однако в реальных задачах оптимизации в силу сложности целевой функции и накладываемых на нее ограничений зачастую бывает очень сложно или даже невозможно не только найти экстремум целевой функции, но даже доказать его существование. В таких случаях под оптимизацией (поиском оптимального решения) понимают так называемый «синтез через анализ» — рассмотрение различных альтернатив и выбор наиболее подходящей из предложенных [1].

Методы нахождения оптимальных решений можно разделить на три основные группы [2-3]:

• -    метод прямого перебора,

• -    методы градиентного спуска,

• -    метод случайного поиска.

В первом случае поиск оптимального решения сводится к перебору всех возможных значений для всех переменных и к сравнению полученного результата с известным критерием. Этот метод является наиболее точным, но и наиболее медленным.

Метод случайного поиска заключается в генерации большого количества случайных решений и вычислении значения целевой функции для каждого из них. Это наиболее быстрый, но наименее точный метод.

Метод градиентного спуска – это разновидность направленного поиска в сторону уменьшения ошибки. При этом вначале выбираются некоторые случайные значения параметров, а затем эти значения постепенно изменяют, добиваясь наибольшей скорости роста целевой функции. Достигнув локального максимума, такой алгоритм останавливается, поэтому для поиска глобального оптимума потребуются дополнительные усилия. Градиентные методы работают очень быстро, но не гарантируют оптимальности найденного решения [2-3]. Их применение оправдано в так называемых унимодальных задачах, где целевая функция имеет единственный локальный максимум (он же – глобальный). Однако на практике встречаются задачи, как правило, мультимодальные и многомерные, то есть содержат большое количество параметров. Для таких задач не существует ни одного универсального метода, который позволял бы достаточно быстро найти абсолютно точное решение [2].

При всем разнообразии данных методов их недостаток – слишком большое время обработки данных (особенно при большом количестве переменных и/или сложной форме N-мерной абстрактной «поверхности», описываемой совокупностью ограничений целевой функции) и, соответственно, необходимость в больших вычислительных ресурсах, требуемых для решения подобных задач.

Комбинируя различные методы, можно надеяться получить хотя бы приближенное решение, точность которого будет возрастать при увеличении времени расчета. Одним из таких комбинированных методов является генетический алгоритм.

Генетический алгоритм – это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путем случайного подбора, комбинирования и вариации параметров (аргументов целевой функции) с использованием механизмов, напоминающих биологическую эволюцию [2-4]. Основателем данного метода считается Дж. Холланд [3-5], работа которого [5] считается основополагающим трудом в этой области.

Задача при данном подходе формализуется таким образом, чтобы ее решение могло быть закодировано в виде вектора генов («генотипа»), где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях предполагается, что генотип имеет фиксированную длину. Однако существуют вариации генетических алгоритмов, свободные от этого ограничения.

Некоторым, обычно случайным, образом создается множество генотипов начальной популяции. Они оцениваются с использованием «функции приспособленности», в результате чего с каждым генотипом ассоциируется определенное значение «приспособленности», которое определяет, насколько хорошо «особь», им описываемая, решает поставленную задачу.

Из полученного множества решений («поколения») с учетом значения «приспособленности» выбираются решения (обычно лучшие особи имеют большую вероятность быть выбранными), к которым применяются «генетические операторы» (в большинстве случаев «скрещивание» и «мутация»), результатом чего является получение новых решений. Для них также вычисляется значение приспособленности и затем производится отбор («селекция») лучших решений в следующее поколение.

Эти действия повторяются итеративно, моделируя таким образом «эволюционный процесс», продолжающийся несколько жизненных циклов (поколений), пока не будет выполнен критерий остановки алгоритма. Таким критерием может быть:

• -    найденный глобальный экстремум;

• -    исчерпание числа поколений, отпущенных на эволюцию;

• -    исчерпание времени, отпущенного на поиск решения.

Обобщенная схема генетического алгоритма представлена на рис. 1.

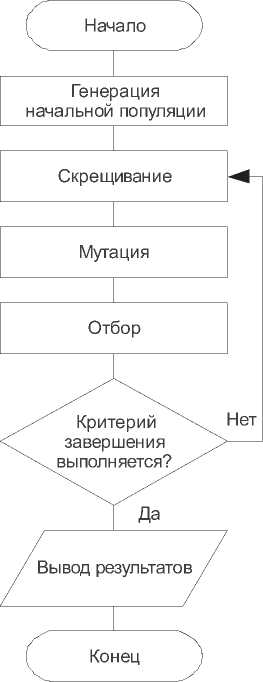
Рис. 1. Обобщенная схема генетического алгоритма

На первом шаге случайным образом создается начальная популяция. При этом можно особенно не стараться сделать слишком уж приспособленных особей, достаточно, чтобы они соответствовали формату особей популяции и для них можно было вычислить значение приспособленности.

Скрещивание в разных алгоритмах осуществляется по-разному и зависит от формата представления данных. Главное требование – чтобы потомки имели возможность унаследовать черты обоих родителей, «смешав» их каким-либо способом.

Основной проблемой многих генетических алгоритмов является достаточно быстрое выделение единственного генотипа, который представляет собой локальный максимум, после чего все остальные особи популяции проигрывают ему отбор, и вся популяция заполняется копиями этой особи. Один из способов борьбы с таким нежелательным эффектом – выбор для размножения не самых приспособленных, но вообще всех особей.

На шаге мутации выбирается часть особей, которые затем изменяются в соответствии с заранее определенными операциями.

На этапе отбора из всей популяции выбирается определенная доля особей, которая останется «в живых» на этом этапе эволюции. Существуют разные способы проведения отбора, но в любом случае вероятность выживания особи должна зависеть от значения функции приспособленности. Хотя обычно доля выживших является параметром генетического алгоритма, и ее просто задают заранее. Особи, не прошедшие отбор, исключаются из популяции.

Оптимизация бизнес-процессов

Применение описанного подхода для подбора значений параметров имитационной модели биз-нес-процесса позволяет очень быстро определить параметры управляющего воздействия, которое было бы наиболее эффективным для достижения поставленной цели.

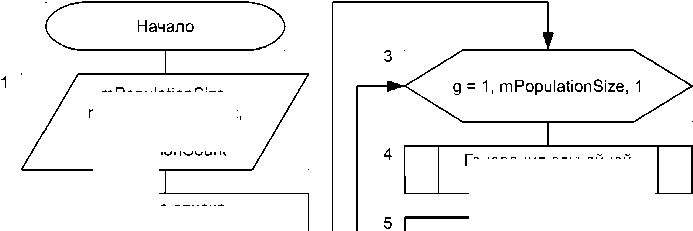
На рис. 2 приведен пример простого генетического алгоритма, который может быть применен для оптимизации бизнес-процессов.

В блоке 1 осуществляется ввод параметров алгоритма: размер популяции ( mPopulationSize ), количество поколений ( mGenerationsCount ), количество особей, выживающих при отборе ( mSelectionCount ), и количество особей, подвергаемых мутации ( mMutationCount ).

В блоке 2 подготавливается список mSpecies , который будет содержать особей популяции (возможные решения).

Блоки 3-5 описывают цикл генерации начальной популяции, в котором список mSpecies заполняется произвольными решениями.

Блоки 6-23 задают цикл формирования новых поколений.

Добавление rndjnd в список mSpecies

Очистка списка mSpecies

Генерация случайной особи rnd ind

mPopulationSize, mGenerationsCount, mSelectionCount, mMutationCount

Копирование результатов в модель з наилучшей особи

в список children

Добавление children в список mSpecies

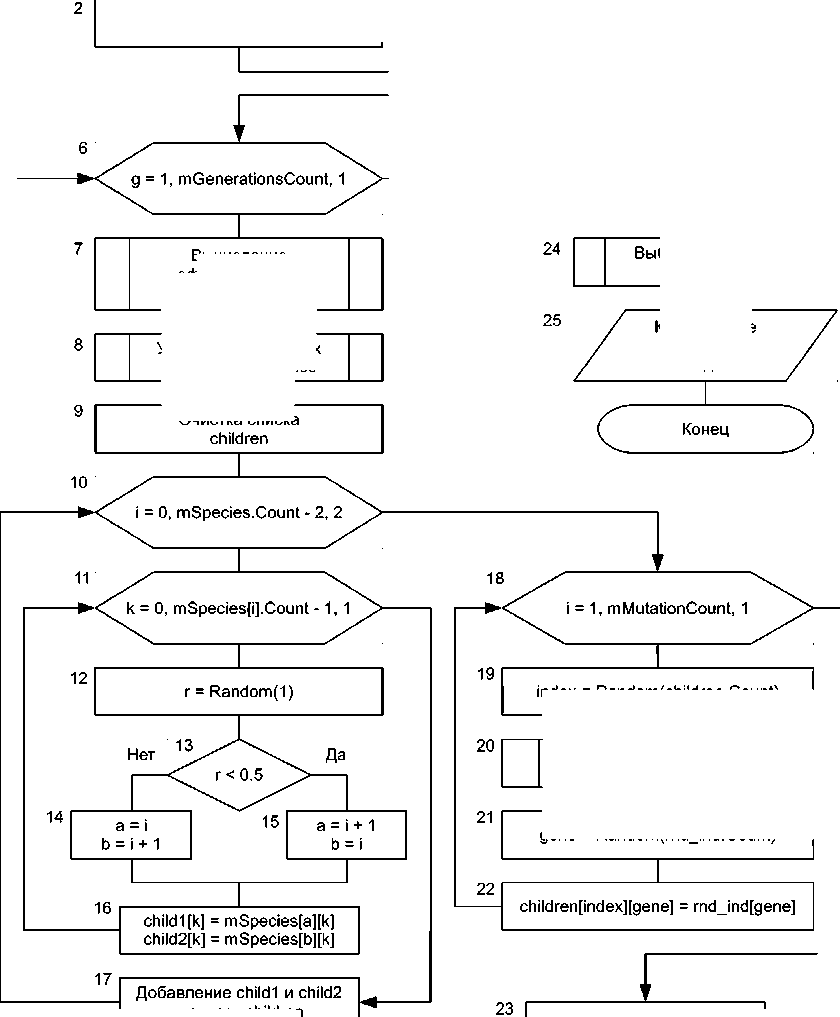
Рис. 2. Обобщенная схема генетического алгоритма оптимизации бизнес-процесса

Вычисление эффективности каждой особи

Удаление наихудших особей из mSpecies

Очистка списка

index = Random(children. Count)

Генерация случайной особи rndjnd

Блок 7 представляет собой процедуру вычисления значения эффективности каждого решения из списка mSpecies . Для этого значения параметров отдельных элементов модели задаются в соответствии с оцениваемым решением, после чего производится моделирование. Результатом моделирования является ряд статистических данных, на основе которых вычисляется значение критерия эффективности данного решения.

В блоке 8 из списка mSpecies удаляются решения с наихудшими значениями критерия эффективности. В результате в списке остается mSelectionCount записей.

В блоке 9 подготавливается список children , который будет содержать особей нового поколения.

Блоки 10-17 описывают цикл попарного скрещивания соседних особей из списка mSpecies .

Блоки 18-22 задают цикл мутации. Из всей популяции случайным образом выбираются mMutationCount особей (обычно около 2%). После чего у каждой из этих особей случайным образом выбирается ген, значение которого меняется на величину, случайным образом выбранную из множества допустимых значений.

В блоке 23 новое поколение объединяется с остальными особями популяции, после чего начинается формирование очередного поколения.

Этот процесс повторяется до тех пор, пока количество поколений не достигнет mGenerationCount . После того как сформируется последнее поколение, из всей популяции выбирается особь с наивысшим значением критерия эффективности (блок 24), параметры которой выводятся в качестве найденного решения (блок 25).

Рассмотрим в качестве примера процесс производства штучных изделий из готовых стандартных комплектующих. Примером подобного процесса может служить процесс производства пластиковых окон и дверей. Перед руководством таких компаний нередко встает вопрос: насколько агрессивной должна быть рекламная политика, чтобы максимизировать количество заказов, не превышая при этом существующие производственные мощности? Имея имитационную модель производственного процесса и применив к ней приведенный выше алгоритм, можно без труда получить параметры потока заказов, который бы обеспечивал квазиоптимальную загрузку оборудования.

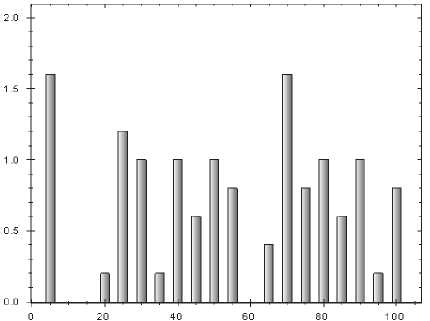
Рис. 3. Динамика выработки продукции до оптимизации рекламной политики

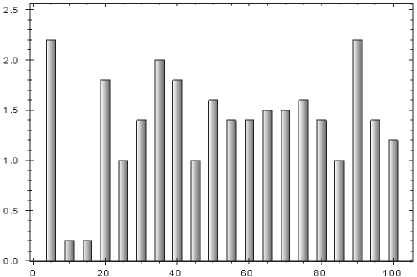
Рис. 4. Динамика выработки продукции после оптимизации рекламной политики

На рис. 3-4 приведены усредненные графики выработки продукции в тестовой модели до и после определения при помощи генетического алгоритма квазиоптимальных параметров потока заказов.

Очевидно, что после оптимизации продуктивность предприятия выросла без каких бы то ни было изменений производственного процесса. Впоследствии, основываясь на этих данных, можно грамотно оценить размер бюджета рекламной кампании.

Заключение

Приведенный алгоритм позволяет очень быстро определить параметры управляющего воздействия, которое было бы наиболее эффективным для достижения поставленной цели. Важным достоинством данного подхода является возможность его применения при оптимизации любых бизнес-процессов, независимо от их сложности и количества накладываемых на него ограничений.