Применение генетического алгоритма для решения задачи покрытия множеств

Введение. Задача о покрытии множества является классическим вопросом информатики и теории сложности. Данная задача обобщает NP-полную задачу о вершинном покрытии (и потому также является NP -сложной).

К задаче о покрытии можно свести многие задачи дискретной оптимизации: стандартизации, упаковки и разбиения множества, построения расписаний. Известна также и обратная сводимость задачи о покрытии к этим задачам.

На практике задачи о покрытии возникают при размещении пунктов обслуживания, в системах информационного поиска, при назначении экипажей на транспорте, проектировании интегральных схем и конвейерных линий и т. д.

Постановка задачи. Дано множество U из n элементов, и набор подмножеств U , S = { S ₁,…, S_k }. Каждому подмножеству S i сопоставлена некоторая неотрицательная стоимость c : S → Q⁺ . S' ⊆ S является покрытием, если любой элемент из U принадлежит хотя бы одному элементу из S' [1].

Задача о покрытии множествами заключается в нахождении набора подмножеств, покрывающего все множество U и имеющего минимально возможный вес (в случае взвешенной задачи) или минимально возможное число подмножеств (в случае невзвешенной задачи).

Для упрощения понимания задачи рассмотрим следующий пример. Необходимо собрать команду специалистов для корабля. Члены команды должны обладать в совокупности всеми требуемыми навыками, но количество членов команды должно быть минимальным. Это невзвешенная задача покрытия, т. е. «вес» каждого члена группы оди- наков и поэтому не важен. Если же каждому члену команды поставить в соответствие какую-то величину (вес), например, опыт работы, то задача станет взвешенной.

Можно представить задачу в матричном виде [2]. Пусть А =( a ij ) — произвольная матрица размера m x n с элементами a ij £ {0,1} без нулевых строк и столбцов. Будем говорить, что в А строка i покрывается столбцом j , если a ij =1. Подмножество столбцов называется покрытием, если в совокупности они покрывают все строки матрицы А . Пусть каждому столбцу поставлено в соответствие положительное число c j , называемое весом столбца. Требуется найти покрытие минимального суммарного веса. Вводя переменные X j , равные 1, если столбец j входит в искомое покрытие, и равные 0 в противном случае, приходим к следующей формулировке задачи о покрытии:

• У c j x j ^ min, j = 1

при ограничениях

n

У a ij X j >  1, i = 1,..., m , x j e {0,1}, j = 1,..., n. j = 1

Обзор алгоритмов решения. Для решения задачи покрытия множеств разработано множество алгоритмов, которые можно разделить на следующие классы: приближенные алгоритмы с априорной оценкой, эвристические алгоритмы, точные алгоритмы [3].

Одним из первых приближенных алгоритмов является жадный алгоритм. Для задачи о покрытии с произвольными весами В. Хватал предложил модификацию жадного алгоритма. Поскольку эвристики носят вероятностный характер, их сложность невозможно оценить априорно. К ним можно отнести методы лагранжевой релаксации, генетические алгоритмы, поиск с запретами, алгоритмы муравьиной колонии, нейронные сети. Примером точных алгоритмов служит метод ветвей и границ.

В данной статье авторы рассматривают жадный алгоритма Хватала, модифицированную модель Голдберга генетического алгоритма и эвристику, разработанную Нгуеном М. Х. Кроме того, показано, насколько результаты работы модифицированной модели Голдберга близки к точному решению, полученному с помощью алгоритма точного перебора.

Жадный алгоритм. В 1979 году В. Хватал предложил жадный алгоритм для задачи о покрытии множествами [4, 5].

Алгоритм Хватала ( U , S , c : S ^ Q + ):

• 1)    C ^ 0 , Sol ^ 0 ;

• 2)    While C Ф U do:

Найти S i e S - Sol , у которого a i = c ( S i )/| S i - C | минимально. Sol ^ Sol U { S i }.

C ^ С U S i ( S i - самое эффективное), price ( e ) = a i для всех e e S i - C.

• 3)    Output ( Sol ).

Рассмотрим принцип работы этого алгоритма. На каждой итерации выбираем самое эффективное множество, удаляем покрытые элементы и продолжаем до тех пор, пока не будут покрыты все элементы. Пусть С — это множество элементов, уже покрытых на предыдущих итерациях. Для каждого множества S i определим его эффективность как a_i=c(S i )/|S_l— C|. Эффективность множества равна средней стоимости, с которой покрываются элементы этого множества, еще не покрытые на предыдущих итерациях.

Генетический алгоритм. Общая схема работы. Предложенные в 1975 году Джоном Холландом генетические алгоритмы (ГА) основаны на принципах естественного отбора и наследования и относятся к стохастическим методам [6-9]. Эти алгоритмы успешно применяются в различных областях деятельности (экономика, физика, технические науки и т. п.), их используют для решения многих оптимизационных задач. На рис. 1 представлена общая схема работы ГА.

Применение генетического алгоритма для решения задачи покрытия множеств. Представленная схема является общим алгоритмом для решения многих задач, и при применении её к конкретной задаче необходимо выбрать механизм кодирования параметров в гены особи, оптимизационную функцию, условие останова [1]. Авторы модифицировали модель Голдберга и применили ее для решения задачи покрытия множеств. В данном случае оптимизационной функцией будет являться минимизация веса покрытия, а условием останова будет неизменность лучшего решения в течение заданного числа поколений.

Рассмотрим механизм кодирования особи. Каждый индивид k представлен хромосомой, являющейся n -мерным вектором x^k , у которого j -й элемент x^k j принимает значение 1, если подмножество S j входит в покрытие, и принимает значение 0, если иначе.

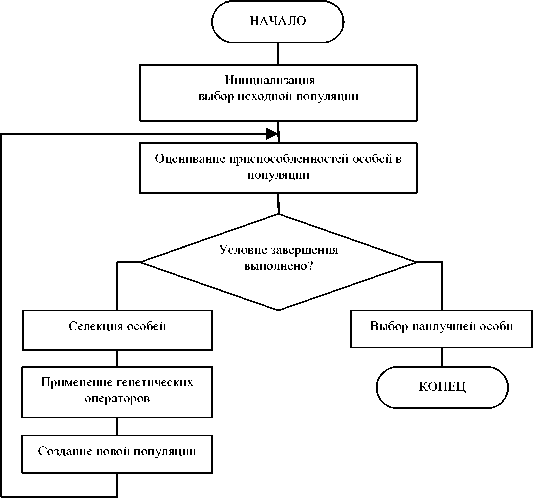
Рис. 1. Общая схема ГА

С таким представлением степень приспособленности f_k индивида x^k может быть рассчитана следующим образом:

ⁿ fk = ^ c J x J , J = 1

где c j — стоимость подмножества S j .

Таким образом, оптимизационная функция выглядит как f_k ^ min .

Для выбора родительских особей используется случайный отбор. В алгоритме используется тип мутации, основанный на изменении случайного гена на противоположное значение. Оператор скрещивания точечный. Выбираются пары хромосом из родительской популяции. Далее для каждой пары отобранных таким образом родителей разыгрывается позиция гена (локус) в хромосоме, определяющая так называемую точку скрещивания — l k . В результате скрещивания пары родительских хромосом получается следующая пара потомков: P 1 — потомок, хромосома которого на позициях от 1 до l_k состоит из генов первого родителя, а на позициях от l_k + 1 до L — из генов второго родителя; P 2 — потомок, хромосома которого на позициях от 1 до l_k состоит из генов второго родителя, а на позициях от l k + 1 до L — из генов первого родителя.

Начальное поколение состоит из особей, сформированных случайно с помощью алгоритма, подобному жадному алгоритму.

Очень важная деталь работы генетического алгоритма в том, что при скрещивании и мутации могут появиться особи, соответствующие покрытия которых не существуют, то есть получаются недопустимые решения. Алгоритм проверяет, существует ли покрытие, и если нет, то пытается, в случае скрещивания, выбрать другую вторую родительскую особь, а в случае мутации — выбрать другой ген для его инвертирования. Если и это не «исправит» особь, родитель выбирается заново случайным образом. Потомок заменяет случайно выбранную особь, если его приспособленность выше.

Рассмотрим на примере, как работает генетический алгоритм и как он избавляется от недопустимых решений. Задача представлена в виде матрицы размером 10x10, заполненной "0" и "1". Столбцы матрицы — это подмножества множества U , а строки — элемента множества U . Таким образом, множество U = {x₀,...,x₉}, и оно состоит из 10 подмножеств S={S 0 ,...,S 9 }. "1" в матрице обозначает, что соответствующее столбцу подмножество покрывает соответствующий строке элемент. Не будем учитывать веса подмножеств, т. е. задача невзвешенная.

0	1	0	0	1	0	1	1	1	1
1	0	1	0	1	1	0	0	1	0
0	1	0	1	0	0	1	1	0	1
1	0	1	0	1	1	0	1	0	0
1	1	0	1	0	1	1	1	0	0
0	0	1	1	0	0	0	0	0	1
1	0	0	0	1	0	1	0	1	0
0	0	1	0	1	0	0	0	0	1
0	0	1	1	1	1	0	1	0	1
0	1	1	0	1	0	1	1	1	1

S 0 S 1 S 2 S 3 S 4 S 5 S 6 S 7 S 8 S 9

Рис. 2 Матрица подмножеств исходного множества

Используем для поиска покрытия наименьшей мощности ГА с 10 особями.

Каждая особь соответствует определенному покрытию, поэтому длина особи равна 10 и каждый ген Ch={Ch 0 ,...,Ch 9 } соответствует определенному подмножеству. Если ген особи равен "1", то подмножество входит в покрытие, если "0", то не входит.

На начальном шаге алгоритма особи формируются случайным образом. Представим особи и их гены в виде массива, где строка — особь, столбец — ген особи.

особь 0	1	1	1	0	0	0	0	0	0	0
особь 1	1	0	0	0	1	0	0	0	0	1
особь 2	1	0	0	1	0	1	0	0	0	1
особь 3	1	1	1	0	0	0	0	1	0	0
особь 4	0	0	0	1	1	0	1	0	0	0
особь 5	1	0	0	1	1	0	0	0	0	0
особь 6	0	0	0	0	0	0	0	0	0	0
особь 7	1	0	1	0	0	1	0	1	0	1
особь 8	0	0	0	1	1	0	1	1	0	0
особь 9	1	1	1	0	0	1	0	0	1	0
	Ch 0	Ch 1	Ch 2	Ch 3	Ch 4	Ch 5	Ch 6	Ch 7	Ch 8	Ch 9

Рис. 3 Формирования начальной популяции

На следующем шаге случайно выбрана родительская особь "1". С некоторой вероятностью к ней применяется оператор одноточечного скрещивания, поэтому случайно выбирается вторая родительская особь "2". Точка скрещивания = ген №3. После скрещивания получаем потомка:

1

0

0

0

0

1

0

0

0

1

Покрытие, соответствующее этому потомку, существует. С некоторой вероятностью к потомку применяется оператор одноточечной мутации. Случайным образом выбран ген №9, он меняет свое значение на противоположное.

1

0

0

0

0

1

0

0

0

0

Но такого покрытия не существует, алгоритм пытается выбрать другой ген, выбран ген №2. Особь-потомок:

1

0

1

0

0

1

0

0

0

1

Такое покрытие существует. Далее в поколении случайно выбирается особь №9, которую, возможно, заменит потомок. Приспособленность потомка равная 4 выше приспособленности особи №9 равной 5 , поэтому он ее заменяет.

Все описанные шаги выбора родительских особей и применения к ним операторов скрещивания и мутации повторяются, пока не будет найдено решение. Алгоритм заканчивает свою работу, если решение не может быть улучшено за заданное число поколений.

Модификация генетического алгоритма Нгуена Минь Ханга. В статье [10] Нгуен Минь Ханг показал свой подход к решению задачи покрытия множеств, основанный на генетическом алгоритме. Особенностью данного подхода является использование модифицированной для задачи покрытия классической модели ГА. Для выбора родительских пар используется метод пропорционального отбора. Каждой особи ставится в соответствие вероятность выбора этой особи, рассчитанная по ее эффективности. Разработан новый оператор кроссовера, суть которого в том, что соответствующий ген для особи-потомка определяется в зависимости от степени приспособленности родителя и от частоты появления этого гена в популяции. Кроме того, используется переменная частота мутации. При применении операторов кроссовера и мутации над индивидами допустимость решения может быть нарушена (т. е. полученный набор не является покрытием множества). Для устранения этого явления предлагается эвристический алгоритм восстановления допустимости решения, одновременно являющийся локальным оптимизационным шагом для увеличения общей эффективности генетического алгоритма.

Анализ производительности алгоритмов. Исследуем вопрос, какой алгоритм получает более точные решения, Голдберга или Нгуена М. Х. В целях сравнения эффективности этих алгоритмов по весам найденных покрытий и временным затратам было разработано программное средство на языке C#. Представлены результаты экспериментов на ПК следующей конфигурации: ОС Microsoft Windows 10 Pro x64, процессор Intel(R) Core(TM) i5-2500K CPU 3.30 GHz , оперативная память 6 Гб. Было проведено по 100 экспериментов с различными матрицами размером n x m , где n — количество подмножеств множества U , m — мощность (количество элементов) множества U . Матрицы заполняются случайным образом "0" и "1".

• •    Коэффициент заполненности матрицы подмножеств единицами p =0.5.

• •    Интервал распределения весов подмножеств для взвешенной задачи 1…200 (целые числа), формируются

случайным образом.

• •    Количество подмножеств и количество элементов множества U принимает значения 30x30, 50x50, 100x100, 150x150, 200x200

Приведены результаты сравнения модели Голдберга с различным числом особей (50, 100, 150, 200), жадного алгоритма Хватала и эвристики Нгуена М. Х. (50, 100, 150, 200 особей). Параметры для ГА были заданы следующие:

• •    вероятность скрещивания = 1,

• •    вероятность мутации = 1,

• •    условие останова =100 поколений,

• •    тип оператора скрещивания — одноточечное,

• •    тип мутации — одноточечная.

Результаты сравнения алгоритмов для взвешенной задачи по весам покрытий представлены в таблице 1, по времени работы — в таблице 2, для невзвешенной задачи — в таблицах 3 и 4 соответственно.

Таблица 1

Веса покрытий (взвешенная задача)

Алгоритм	30х30	50х50	100х100	150х150	200х200
ГА 50	88,57	65,67	48,98	40,97	32,72
ГА Нгуен50	91,66	67,44	53,67	51,92	50,84
ГА 100	88,51	63,12	46,3	39,57	31,99
ГА Нгуен100	90,34	66,13	49,36	43,58	42,5
ГА 150	87,22	62,76	45,93	38,95	31,25
ГА Нгуен150	89,78	65,71	49,44	41,97	40,21
ГА 200	87,05	62,83	46,22	38,35	30,74
ГА Нгуен200	88,94	65,57	49,54	41,47	38,81
Жадный	98,14	74,56	70,66	91,99	110,24

Таблица 2

Алгоритм	30х30	50х50	100х100	150х150	200х200
ГА 50	254,2886	751,8143	3806,738	9814,355	19801,82
ГА Нгуен50	1850,67	1844,317	1881,946	1957,975	3506,081
ГА 100	488,2043	1387,882	7508,047	18293,5	35186,1
ГА Нгуен100	1931,191	2020,152	2308,606	4333,37	5555,818
ГА 150	703,5788	2036,386	10085,16	25527,69	49748,35
ГА Нгуен150	2065,456	2040,725	2381,178	4973,016	8947,126
ГА 200	926,0862	2684,479	12662,96	32821,01	65370,57
ГА Нгуен200	2075,047	2147,794	5029,717	8576,225	12329,05
Жадный	0,101141	0,216815	0,922629	2,186599	4,014783

Таблица 3

Алгоритм	30х30	50х50	100х100	150х150	200х200
ГА 50	2,96	3,23	4,17	4,84	5,1
ГА Нгуен50	3,28	3,94	4,93	5,45	5,89
ГА 100	2,97	3,12	4	4,71	4,98
ГА Нгуен100	3,05	3,78	4,76	5,26	5,69
ГА 150	2,96	3,03	3,93	4,59	4,98
ГА Нгуен150	3,01	3,73	4,61	5,1	5,62
ГА 200	2,96	3	3,95	4,47	4,92
ГА Нгуен200	3,01	3,7	4,54	5,04	5,61
Жадный	4,66	5,44	6,49	6,92	7,48

Таблица 4

Временные затраты работы алгоритмов в мс (невзвешенная задача)

Алгоритм	30х30	50х50	100х100	150х150	200х200
ГА 50	202,2554	565,297	2066,982	4261,727	7823,984
ГА Нгуен50	1612,93	1629,785	1603,908	1712,292	2627,43
ГА 100	401,6485	1181,412	3979,194	8521,661	14765,89
ГА Нгуен100	1608,363	1651,991	1668	3300,692	4343,407
ГА 150	582,8104	1625,455	5838,935	12848,03	20946,68
ГА Нгуен150	1612,511	1665,563	1679,632	3421,566	5561,238
ГА 200	770,9581	2138,706	7388,203	17932,41	28690,47
ГА Нгуен200	1604,523	1674,239	3351,328	4862,393	6814,878
Жадный	0,102653	0,2312	0,946716	2,236784	4,10912

Временные затраты работы алгоритмов в мс (взвешенная задача)

Веса покрытий (невзвешенная задача)

Алгоритм полного перебора (брутфорс). Полный перебор ( brute force ) — метод решения математических задач. Относится к классу методов поиска решения исчерпыванием всевозможных вариантов. Сложность полного перебора зависит от количества всех возможных решений задачи.

Любая задача из класса NP может быть решена полным перебором. При этом, даже если вычисление целевой функции от каждого конкретного возможного решения задачи может быть осуществлено за полиномиальное время, в зависимости от количества всех возможных решений полный перебор может потребовать экспоненциального време ни работы.

Суть алгоритма полного перебора для решения задачи покрытия заключается в переборе всех возможных сочетаний разной длины подмножеств исходного множества и, если очередное сочетание является покрытием и его вес минимален, необходимости сохранить его. Из теории множеств известно, что число всех подмножеств множества из n элементов равно 2 ⁿ . Другими словами

n

E C k = 2 ⁿ .

k = 0

Итак, чтобы получить точное решение задачи размерности 25x25, пришлось перебрать 225=33554432 вариантов, для этого потребовалось около 2–3 часов, но задача немного большей размерности 30x30 включает 230=1073741824 вариантов, что уже затруднительно для расчетов.

Для ускорения полного перебора программное средство было модифицировано для распараллеливания вычислений с помощью многопоточности.

Решения, полученные модификацией модели Голдберга с 200 особями, были сравнены с точными решениями, полученными брутфорсом, в задачах размерности до 25x25. Усредненные результаты по 100 экспериментам взвешенной задачи приведены в таблице 5.

Таблица 5

Веса покрытий точного решения и ГА

nxm	ГА	Точное решение
20x20	108,01	107,95
25x25	88,94	88,02

Заключение. Проведено сравнение производительности различных алгоритмов применительно к взвешенной и невзвешенной задачам покрытия множеств. Обе модификации генетического алгоритма намного превосходят жадный алгоритм по весовым показателям получившихся покрытий, но по параметру трудоемкости жадный алгоритм выигрывает с огромным отрывом. Если важна скорость вычислений, то в задачах небольшой размерности можно использовать жадный алгоритм. Чем больше особей в поколении использует ГА, тем лучше результат весов покрытий. ГА с 200 особями лучший из рассмотренных. Но, естественно, чем больше особей, тем дольше работает алгоритм. По сравнению с эвристикой Нгуена М. Х. модифицированная модель Голдберга показывает лучшие результаты, что более заметно в задачах большой размерности, но при этом она использует больше временных ресурсов, ведь операторы скрещивания и мутации с вероятностью 100% применяются для всех особей поколения поочередно, в отличие от механизма Нгуена М. Х. Кроме того, в задачах небольшой размерности ГА на основе модели Голдберга получает решения, очень близкие к точным.