Применение ГИС-технологий для повышения эффективности имитационного моделирования каскадов ГЭС

Имитационное моделирование (англ. simulation modeling) – метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью описывающей реальную систему (построенная модель описывает процессы так, как они проходили бы в действительности), с которой проводят эксперименты для получения информации об этой системе.

Имитационное моделирование в настоящее время достигло широкого распространения и встречается в разнотипных исследованиях: бизнес-процессы, динамика населения, дорожное движение, железнодорожные перевозки, рынок и конкуренция, здравоохранение, машиностроение и мн. др. Если объектом управления выступает каскад ГЭС, моделирование процессов должно учитывать не только различные алгоритмы управления этим объектом, но и изменяющиеся входные параметры, диктуемые природными условиями.

В теории имитационного моделирования выделяют три основных метода: дискретно-событийное моделирование, агентное моделирование и системная динамика. При сложных исследуемых системах могут использоваться многоподходные модели.

Гидроэлектростанции (ГЭС) относятся к сложным, искусственно созданным системам открытого типа со специфическими свойствами: вероятностный и неопределенный характер параметров, изменяющихся во времени, тесные взаимосвязи с социальными, экономическими, природными факторами. Сложность производственного процесса, длительность эксплуата-– 733 – ции и изменчивость влияния природных факторов в течение года делают актуальной задачу построения имитационной модели ГЭС. Имитационная модель позволяет заменить натурные эксперименты, «проиграть» и проанализировать множество состояний, скорректировать планирование режимов работы [1].

Авторами разработана имитационная модель, объединяющая гидравлический и электрический режимы электроэнергетической системы [2]. При моделировании режимов работы и состояния водохранилища ГЭС важно использовать достоверную статистическую информацию. Актуальная входная информация, а также ее краткосрочный и долгосрочный прогноз могут быть получены на основе данных системы пространственного мониторинга территории, технологий геоинформационного анализа и моделирования.

Зачастую данные наземных средств наблюдения являются высокозатратными и обеспечивают недостаточную зону покрытия (как в территориальном, так и во временном аспекте). Оптимальным решением проблемы будет использование данных дистанционного зондирования Земли (ДЗЗ). Под данными ДЗЗ, как правило, понимают космические снимки, полученные с искусственных спутников Земли, прошедшие обработку и представляющие из себя растровое изображение поверхности Земли, а также файл с пространственными данными о снимке. Данные ДЗЗ доступны для любой территории и, соответственно, для любой существующей или проектируемой ГЭС. Дополнительным плюсом считают то, что эта информация с точностью, достаточной для проведения научных исследований, представлена в свободном доступе. Данные ДЗЗ могут быть использованы в условиях, когда невозможны наземные методы исследования, например горная местность, удаленные районы, ледниковые отложения и пр. Данные ДЗЗ применяются в качестве основы при создании баз данных для геоинформационных систем (ГИС).

Анализ возможностей ДЗЗ

В рамках настоящего исследования необходимо оценить возможности ДЗЗ с точки зрения применимости при расчете режима каскада ГЭС. А также сузить перечень возможных исходных данных до наиболее значимых параметров для имитационной модели. Схема интеграции ГИС-технологий в имитационную модель представлена на рис. 1.

Условно данные ДЗЗ, имеющие значимость для описываемой задачи, можно разделить на две категории: географические и климатические. К первой категории относятся:

• 1 . Геометрические параметры рельефа. Основываясь на цифровой модели рельефа, средствами геоинформационных систем можно получить ряд производных параметров, комплексно описывающих конкретное место на поверхности Земли:

Рис. 1. Интеграция ГИС-технологий в имитационную модель каскада ГЭС

Fig. 1. Integration of GIS technologies into the simulation model of a cascade of HPP

• –    уклон – величина, определяющая крутизну рельефа и представляющая собой максимальный коэффициент изменчивости текущей ячейки цифровой модели рельефа, относительно соседних ячеек, учитывается, например, при расчете скорости течения воды;

• –    экспозиция – направление по сторонам света, в котором ориентирована плоскость склона для каждой ячейки цифровой модели рельефа, наиболее часто учитывается при определении количества солнечного света, получаемого этим участком склона, либо при направлении стока;

• –    кривизна – величина, показывающая степень вогнутости или выпуклости поверхности, которая используется при расчете положения водосборных бассейнов;

• –    индекс топографической позиции (англ. TPI) – расчетная комплексная величина индекса превышения, позволяющая определять характеристики и классифицировать водоразделы, склоны и элементы рельефа.

Учитывая объект исследования, эти параметры важны при оценке:

• –    объема воды в речной сети,

• –    направления стока,

• –    положения площадей водосбора при выпадении осадков на конкретных территориях,

• –    предполагаемого объема талого снега на основе его положения относительно преобладающего направления солнечного излучения [3] (рис. 2).

• 2 . Геометрические параметры объектов гидрографии. К ним относят площадь водной поверхности и ширину створа. Геометрические параметры объектов гидрографии подвержены

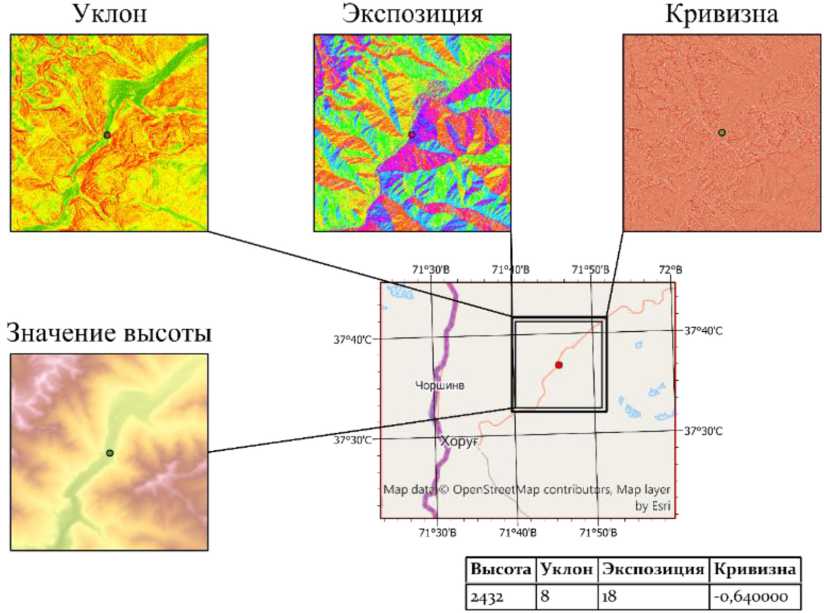
Рис. 2. Пример визуализации параметров рельефа для одного и того же участка местности и числовые значения этих же параметров для указанной точки

Fig. 2. An example of visualization of terrain parameters for the same area and numerical values of the same parameters for a specified point

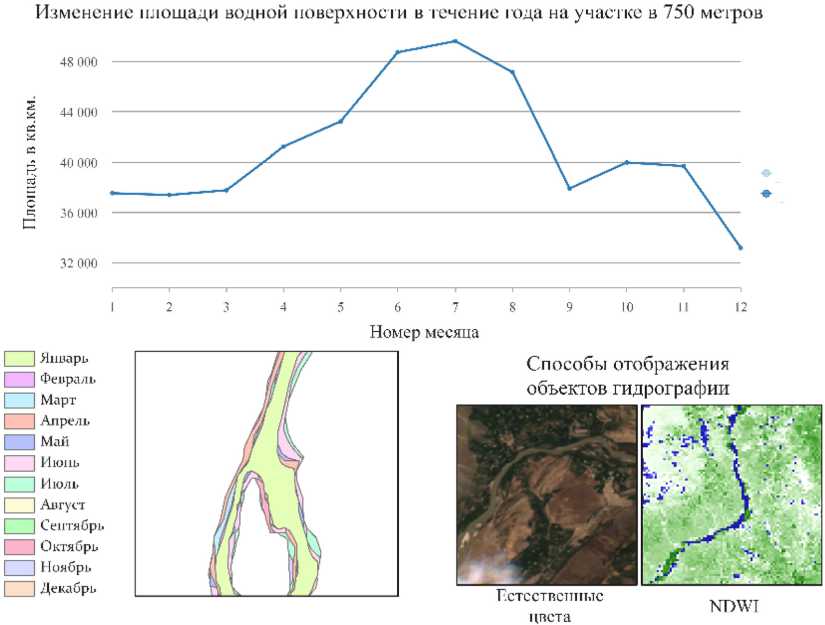
Рис. 3. Визуализация изменения площади водной поверхности, а также способы представления объектов гидрографии для ручного и автоматизированного дешифрирования контура водной поверхности

Fig. 3. Visualization of changes in the surface area of the water surface, as well as methods for representing hydrographic objects for manual and automated interpretation of the water surface contour изменению и будут зависеть от даты исследования. Для расчета геометрических параметров необходимо на спутниковых снимках выделить границы объектов гидрографии, вручную указывая контур либо автоматически сделав выборку пикселей на основе какого-либо алгоритма автоматизированного дешифрирования (рис. 3).

Параметры географической группы являются базовыми. Объединив их, можно получить дополнительную систему гидрологических параметров (водотоки, направления стока и точки кумулятивного стока, водосборные бассейны), которые также могут быть использованы при построении имитационной модели каскада ГЭС.

Ко второй категории относятся:

• 1.    Температура. В расчетах могут быть использованы два варианта – температура воздуха, получаемая с метеорологических постов, и температура земной поверхности, получаемая по спутниковым снимкам на основе термальных спектральных каналов [4, 5] (рис. 4).

• 2.    Интенсивность осадков на основе микроволновой радиометрии [6-8].

• 3.    Количественные показатели снежного покрова территорий, формирующих сток анализируемой реки: площадь снежного покрова и его толщина, основано на косвенном параметре водного эквивалента (рис. 5). Эти показатели важны для среднесрочного и долгосрочного прогнозирования [9].

Возможные исходные данные сведены в табл. 1. Также нужно отметить, что поскольку все описанные выше параметры основываются на данных растрового представления, то для базовой оценки их плановой точности указано разрешение.

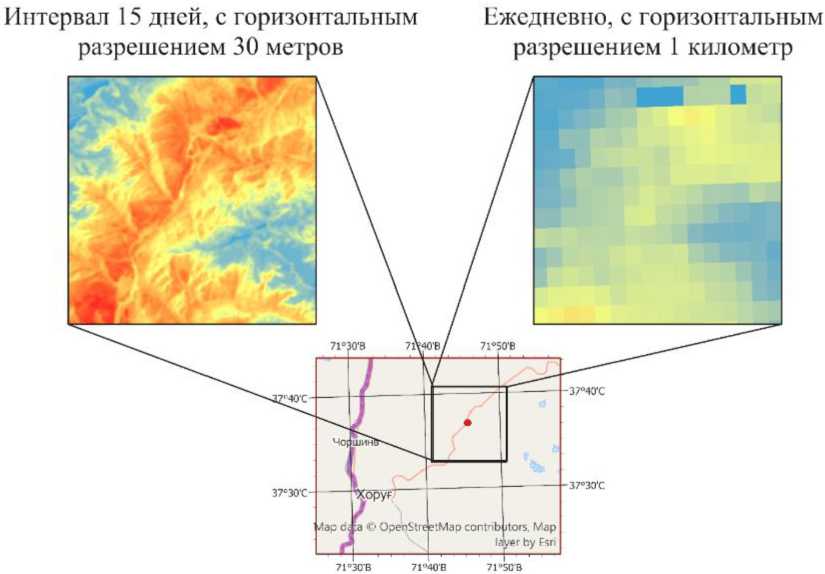
Рис. 4. Визуальное представление данных о температуре земной поверхности одного и того же участка территории для разного временного разрешения

Fig. 4. Visual presentation of data on the earth’s surface temperature of the same area for different time resolutions

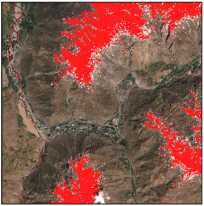
Площадь снежного покрова:

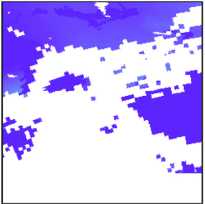
Толщина снежного покрова:

- ежедневно с горизонтальной точностью в 5 км.

• -    с интервалом в 15 дней с точностью 15 метров;

• -    ежедневно, с точностью 500

метров.

Рис. 5. Визуализация данных о состоянии снежного покрова для одной и той же территории

Fig. 5. Visualization of snow cover data for the same territory

Интеграция ДЗЗ в задачи моделирования режимов ГЭС

Используя географические и климатические данные, нужно учитывать, что большинство из них представляют собой трехмерные матрицы, суммарно содержащие миллионы значений параметров, и применять их в исходном виде для большинства алгоритмов и математических моделей не представляется возможным. Кроме того, исходные данные и их источники выбраны таким образом, чтобы для каждого из критериев и для каждого анализируемого участка местности можно было получить ряд ретроспективных значений. Таким образом, анализируемые данные представлены в виде четырехмерных матриц. Поэтому в исследовании нужно рассмотреть и проанализировать возможные способы снижения размерности каждого из параметров и учета прошлых значений параметров (в виде самих значений, скорости изменения, разницы прогнозного и истинного значений и т.д.).

Таблица 1. Сводная таблица возможных исходных данных

Table 1. Pivot table of possible source data

Группа	Критерий	Единицы измерения	Источник	Разрешение (метры)	Интервал обновления
s Рн c5 Ph C S ¥ s о сЗ Рн О £	Высота над уровнем моря	Метры	Alos Palsar Sentinel S1A	12,5 22	2007 год Ежемесячно
	Уклон	Градусы или проценты	Alos Palsar Sentinel S1A	12,5 22	2007 год Ежемесячно
	Экспозиция	Азимут в градусах	Alos Palsar Sentinel S1A	12,5 22	2007 год Ежемесячно
	Кривизна	Коэффициент кривизны в интервале значений от -4 до +4	Alos Palsar Sentinel S1A	12,5 22	2007 год Ежемесячно
	TPI	Классы типов рельефа	Alos Palsar Sentinel S1A	12,5 22	2007 год Ежемесячно
	Площадь водной поверхности	Квадратные метры	Sentinel-2 Landsat 8	10 15	Ежемесячно Ежемесячно
	Ширина створа	Метры	Sentinel-2 Landsat 8	10 15	Ежемесячно Ежемесячно
s у s У ty «	Температура поверхности Земли	Градусы Цельсия	MODIS Landsat 8	1000 30	Ежедневно Ежемесячно
	Интенсивность осадков	Мм/ч	REMSS	50	Ежедневно
	Площадь снежного покрова	Квадратные метры	MODIS Sentinel-2	500 15	Ежедневно Ежемесячно
	Глубина снежного покрова	Мм	Copernicus	5000	Ежедневно

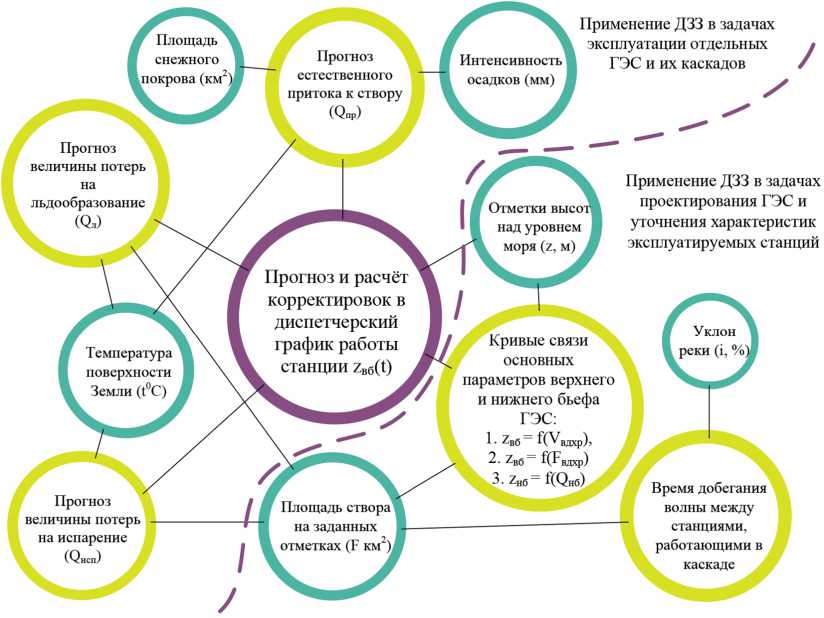
Данные ГИС-мониторинга дают точную и актуальную информацию о гидрологических, гидрографических и климатических параметрах реки с высокой периодичностью обновления. На этапе проектирования применение ГИС-технологии позволит увеличить точность расчета конструктивных параметров ГЭС и емкости водохранилища. Во время эксплуатации ГЭС применение базы данных ДЗЗ позволит увеличить точность прогнозирования естественного притока к створу ГЭС, а также потерь, обусловленных природными факторами. Неполный список задач, решаемых на основе данных ДЗЗ, приведен на рис. 6.

Рассмотрим их более подробно.

• 1.    Одна из важнейших задач на этапе проектирования ГЭС – определение полезного объема водохранилища станции.

• 2.    Особого внимания также заслуживают данные о кривизне поверхности и расстоянии между станциями. Они могут быть использованы для расчета времени добегания волны от одной ГЭС до другой. Это позволит более точно рассчитывать временные поправки в режиме работы станций, связанных в каскаде. Формула для расчета времени добегания волны

  
  
  

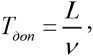
• 3.    На этапе эксплуатации ГЭС особую роль играют задачи краткосрочного и долгосрочного планирования режимов ГЭС. В основе планирования режима лежит прогноз изменения параметров стока, основанный на выявлении закономерностей изменения природных факторов в рамках рассматриваемого интервала времени с применением базы статистической информации за предыдущие этапы наблюдений.

Параметры водохранилища напрямую зависят от рельефа местности, а его площадь может простираться на сотни км2. Использование информации со спутника быстрее, имеет больший охват территории и зачастую точнее традиционных методов позволяет определить зону затопления водохранилища и рассчитать его характеристики.

Применение ГИС-технологий позволит автоматизировать процесс построения кривой связи между уровнем верхнего бьефа (отметка высоты уровня воды перед створом ГЭС) и объемом (площадью) водохранилища. Данная кривая описывает динамику изменения за- – 738 –

Модель прогнозирования

Данные ДЗЗ

Рис. 6. Список задач, решаемых на основе ДЗЗ

Fig. 6. List of tasks solved on the basis of remote sensing

Результаты моделирования

пасов воды и уровня верхнего бьефа ГЭС. Объем воды, срабатываемый или запасаемый в водохранилище, определяет уровень расхода воды через ГЭС, что ведет к изменению мощности и количества вырабатываемой электроэнергии. Эксплуатация гидростанции без заранее определенной кривой связи уровня верхнего бьефа и объема водохранилища невозможна.

Аналогично может быть построена кривая связи между уровнем нижнего бьефа и расходом. Пример построения кривых связи верхнего и нижнего бьефов приведен на рис. 7.

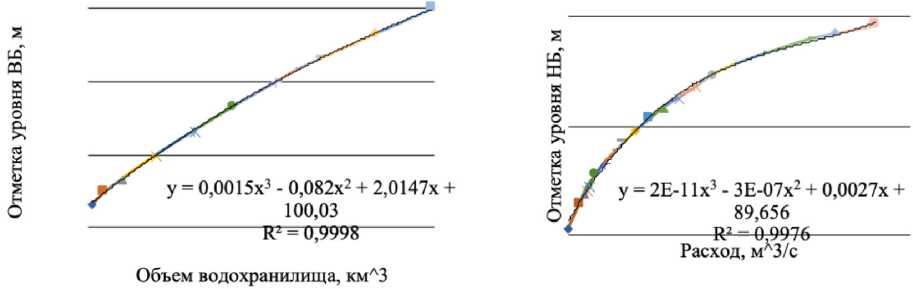
Рис. 7. Кривые связи уровня верхнего и нижнего бьефов на примере Новосибирской ГЭС

Fig. 7. Connection curves of the level of the upper and lower pools on the example of the Novosibirsk HPP

Решение задачи построения кривых связи актуально не только для строящихся гидроэлектростанций. На территории России и стран СНГ имеются гидроэлектростанции, у которых нет точной информации о параметрах собственных водохранилищ, либо данные водохранилищ претерпели изменения за время многолетней эксплуатации. В этом случае мониторинг гидрографических параметров створа позволит скорректировать имеющиеся в распоряжении персонала станции данные, что приведет к повышению эффективности управления режимами станции.

где L - расстояние между первой и второй ГЭС; v - скорость потока.

Скорость движения воды напрямую зависит от уклона реки и гидравлического радиуса русла:

'^f-JVT?. (2)

где С – коэффициент скорости; Rcp – средний гидравлический радиус русла реки на участке между гидроэлектростанциями каскада; Jcp – средний уклон реки.

Так, на основе данных о запасах снежного покрова и изменениях температуры в течение года может быть построена модель прогнозирования притока к створу водохранилища. Данные об изменении площади водохранилища и температуры окружающей среды могут быть использованы для расчета потерь на испарение и льдообразование. Для расчета средних потерь воды на льдообразование можно использовать выражение

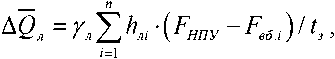
где h_л – толщина льда; γ _л = 0,9 – плотность льда; F – площадь водохранилища при различных отметках; t₃ - продолжительность зимнего периода, определяемая периодом сработки водохранилища.

Потери воды на испарение определяются по формуле

^Qu™ = Xfc -h_ciyF_eJt_ucn>

где ( hвi – hci ) – дополнительный слой испарения, определяемый разностью слоев испарения с поверхности воды зеркала водохранилища h_Bi и с поверхности суши hci , затопленной водохранилищем; tисп – период испарения, обычно соответствующий периоду открытого русла.

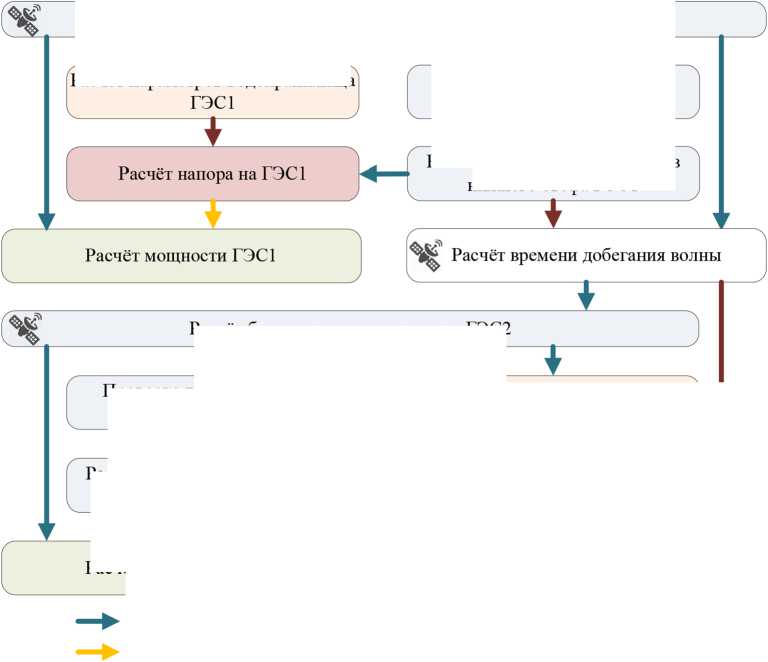
Полученные данные используют для корректировки режима работы станции. Алгоритм расчета режимных параметров ГЭС на основе прогноза притока к створу ГЭС и требований энергосистемы представлен на рис. 8.

Расчёт баланса расходов в створе ГЭС 1

Расчёт параметров водохранилища

Проверка технологических ограничений ГЭС 1

Расчёта и проверка параметров нижнего бьефа ГЭС2

Расчёт баланса расходов в створе ГЭС2

Расчёт напора на ГЭС2

Гидрологические данные

Данные по напору ГЭС

Топографические данные

Данные ГИС-наблюдений

[Расчёт параметров водохранилища ГЭС2

Рис. 8. Алгоритм расчета водно-энергетического режима каскада ГЭС

Fig. 8. The algorithm for calculating the water-energy regime of the cascade of HPP

Расчёта и проверка параметров нижнего бьефа ГЭС1

Проверка технологических ограничений ГЭС2

Расчёт мощности ГЭС2

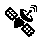
Рассмотрим основные блоки данного алгоритма более подробно.

Блок «Расчет баланса расходов в створе ГЭС»

В данном блоке происходит расчет расхода воды в нижний бьеф через турбины ГЭС и в качестве холостых сбросов, а также задается величина расхода аккумулируемого в водохранилище или забираемого из него. Расчет производится на основе данных о естественном притоке к створу ГЭС и потерь расхода.

Все описанные параметры составляют баланс расходов в створе ГЭС:

Q^Q^QAt^QoAO^^               (5)

Q_HAt^O_r3CU^O_UV                             (6)

о,^п = о_Г!Ст-о,/п±одп+одп-о_Ап-о.^            (7)

где Qпр – естественный приток к створу ГЭС; Qв – расход водохранилища; Qос – осадки на территории водохранилища; Q_ucn - испарение с площади водохранилища; Q_л - потери на льдообразование; Qф – фильтрационный расход через основание ГЭС.

Естественный приток нижележащей станции состоит из расхода вышележащей станции, пропущенного через турбины вышележащей станции и боковой приточности:

.                                                            (8)

^пр.ГЭСл V 7 ЭС1 \ 7 -^бок.пр х 7                                                     ^{х 7}

Как уже было сказано, такие параметры, как естественный приток, потери на льдообразование и т.д., имеют корреляцию с климатическими параметрами в районе ГЭС. В связи с этим появляется возможность разработки балансовых уравнений расхода для прогнозируемых параметров стока на краткосрочные и долгосрочные периоды времени.

Блок «Проверка технологических ограничений ГЭС»

В данном блоке проходит проверка расхода ГЭС на соответствие технологическим и режимным ограничениям.

Q (t)rv(t)                                      (9)

Х-'вхк х 7 ^ГЭС х 7 ^тах                                                            ^{х 7}

В данном выражении Q_BXK(t) - необходимый минимальный расход в нижний бьеф ГЭС для соблюдений требований потребителей водохозяйственного комплекса, Q max - максимально допустимый расход технологическим ограничениям основного силового оборудования. В частности:

Ограничение по пропускной способности турбины:

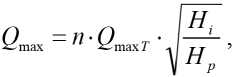
где Q _{max T} – максимальная пропускная способность гидротурбины; H_р – расчетный напор; n – число работающих гидроагрегатов.

Ограничение по установленной мощности генератора:

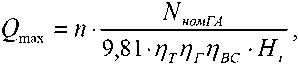
где N_H0MrA - номинальная мощность гидроагрегата; пТПГПВС - кпд турбины, генератора и водоподводящих сооружений.

Блок «Расчет и проверка параметров нижнего бьефа ГЭС»

В данном блоке происходит определение отметки нижнего бьефа в зависимости от суммарного расхода, пропускаемого через гидроагрегаты ГЭС и водосбросные сооружения плотины. Расчет производится на основе зависимости Z_Hf ( Q_h6 ), представленной на рис. 7.

Блок «Расчет параметров водохранилища ГЭС»

В данном блоке определяют отметку верхнего бьефа в зависимости от запасенного объема стока.

Объем, запасаемый в водохранилище или забираемый из него, определяется величиной расхода Q_B :

1'в=1,в(умо)+^й‘*.

Расчет производится на основе зависимости Z_e6f ( V_B ), представленной на рис. 7.

Также в блоке проверяется соблюдение всех ограничений, накладываемых на верхний бьеф водохранилища:

7  <7 < 7

^УМО — во — ^НПУ 1

e6Min eoi вбМах э где Ze6Min - минимальный уровень верхнего бьефа, обусловленный ограничением по гарантированной мощности; Ze6Max - максимальный уровень верхнего бьефа, обусловленный требованиями к оптимальному распределению ресурсов водохранилища при долгосрочном планировании.

Блок «Расчет напора на ГЭС»

Напор на ГЭС определяется как разница между уровнем верхнего и нижнего бьефа с учетом потерь в водоподводящих сооружениях:

h = zs6-zh6-m

В блоке расчета напора на ГЭС 2 также учитывается время добегания расхода от первой ГЭС до второй, что напрямую влияет на уровень верхнего бьефа второй ГЭС.

Блок «Расчет мощности ГЭС»

Расчет мощности производится на основе параметров расхода ГЭС и напора, а также кпд основного силового оборудования станции:

N = 9,S1HQ nTrirriRr гэс ’ Хгэс IT IГ IBC

Блок «Расчет времени добегания волны»

В данном блоке производится расчет времени добегания волны от вышестоящей ГЭС 1 до ГЭС 2.

L-'^Ri-m + L -n? -и

о-^АИ^АИ^У2

где Ri и Ji – гидравлический радиус и уклон участка реки; L – расстояние между ГЭС.

Применение системы ГИС-мониторинга позволяет точно определить географические параметры русла реки между станциями, что дает возможность повысить точность расчета времени добегания и исключить ошибки в расчетах режима нижележащей ГЭС.

Заключение

Планирование долгосрочных и краткосрочных режимов работы электроэнергетических систем с большой долей гидрогенерации неразрывно связано с водно-энергетическим расчетом. Повысить эффективность планов возможно при корректном учете климатических и географических параметров за счет использования ГИС-мониторинга. Создание имитационной модели каскада гидроэлектростанций с интеграцией данных дистанционного зондирования Земли дает преимущества в расчете актуальных параметров ГЭС.