Применение имитационной модели для оптимального распределения ресурсов

Математическое моделирование экономических процессов является важным направлением развития экономической теории и современным инструментом управления как промышленностью в целом, так и предприятием в частности.

Отличительная особенность представленной модели в том, что она является нелинейной и предполагает многоэтапное распределение ресурсов. Рассматриваемая имитационная модель позволяет рассмотреть влияние различных факторов на конечный результат и выбрать оптимальную стратегию распределения ресурсов [1].

Вычислительный алгоритм решения оптимизационной задачи основан на формализации метода динамического программирования.

В многоэтапных моделях выделенный ресурс x распределяется между двумя технологическими процессами: y - для первого процесса, и (x-y) - для второго. При этом первый процесс дает доход за один год φ1(y) и средств остается ψ1(у), а второй процесс дает доход ф2(х - у) и средств остается у2(х - у). N - количество этапов, например N = 5, k - номер этапа.

Остающиеся ресурсы в размере ψk1(у) и ψk2(х–у) можно использовать путем вложения с целью получения дохода на следующем этапе. Таким образом, мы имеем возможность так распределить выделенный ресурс x между процессами по этапам планируемого периода, чтобы полный доход за весь планируемый период принял максимальное значение. Доход, полученный в результате деления ресурса x на величины у и (х - у) на k-ом этапе, обозначим через gk (х, у).

Тогда gк (х,У) = Фк(У) + ф(х - У)

Ресурс, оставшийся для дальнейшего распределения, обозначим через rk (х, у). Тогда тк (х,У) = Фк(х) + Фк(х - У)

Причем должно выполняться ограничение 0 < у < х

Определим функцию fk(x) как полный    доход    от    процесса, начинающегося с величины x на k-ом этапе и заканчивающегося на N-ом этапе при условии, что соблюдается принцип оптимальности.

Тогда при k=N имеем fn (х) = max 0 < у < х д п(х, у)    (1)

и при k=N-1, N-2,...2,1

fk ⁽х) = max o <у <Ад к (*, У) + fk — 1 [г^(х,у)]}   (2)

Это - основные функциональные уравнения, которые использовались для решения задачи синтеза в многоэтапной модели распределения ресурсов.

Факт реинвестирования дохода отражался в связующем соотношении, которое учитывает величину располагаемого ресурса на каждом этапе и определяет переходы на схеме состояний:

Х_к = Р>< д_к(х_к - 1,Ук - 1) + т_к (^к-1,Ук-1) — ^ (%)   (3)

где        p-        коэффициент реинвестирования (0

s(x) – доля погашения кредита или иной платеж.

На коэффициенты и функции, фигурирующие в уравнениях (1)-(3), не накладывается никаких ограничений.

Результат решения задачи синтеза может быть представлен в виде семейства оптимальных траекторий на схеме состояний в координатах k,r.

На рисунке 1 представлен пример трех оптимальных траекторий на схеме состояний.

Для каждой траектории заполняется таблица, пример которой представлен далее (таблица 1).

Оптимальные траектории

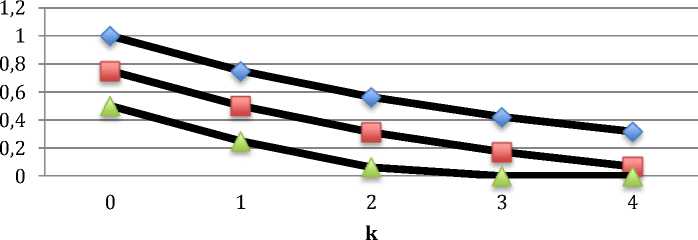
Рис. 1. Семейство оптимальных траекторий на схеме состояний

Таблица 1. Параметры оптимальной траектории

№ этапа k	Вклад в процесс 1	Вклад в процесс 2	Доход f k (x)	Остаток r k (x,y)	Доход g k (x,y)
0	x	-	3,21x	0,75x	x
1	0,75x	-	2,21x	(0,75)2x	0,75x
2	0,5625x	-	1,465x	(0,75)3x	0,5625x
3	0,42x	-	0,9x	(0,75)4x	0,422x
4	-	0,3164x	0,4746x	0,095x	0,475x
	2,7345x	0,3x			3,21x

Данная модель позволяет сделать следующее:

• -задавать различные значения как первоначальному ресурсу, так и ресурсу на промежуточных этапах;

  -изменять               параметры

технологических процессов;

• -задавать различные значения коэффициентов реинвестирования и

• платежей в зависимости от номера этапа.

Кроме того, если построить на схеме состояний семейство траекторий, достаточно близких друг к другу, можно получить значения предельной полезности ресурса tk(rk) в различных точках, используя соотношение tk (rk) = ^f^k гк

В случае постоянных значений p и s и линейных характеристиках ϕ1,ϕ2,Ψ1,Ψ2 можно получить аналитическое решение задачи синтеза в смысле явной зависимости функции f от первоначально выделенного ресурса x.

В дальнейшем можно использовать предельную полезность ресурса – для корректировки оптимального выбора.