Применение информационных технологий для вычисления ранговой корреляции

Значительное место в нефтехимическом образовании захватывают информационные технологии. Преподаватели и студенты в большинстве пользователи ПК, тем более программы пакета Microsoft Office являются широко распространёнными. Значит актуально и обоснованно применение электронных таблиц Excel в решении многообразных расчётных задачах. Данное приложение организовывает работу с базами данных, позволяет вводить математические формулы, применить встроенные функции, реализовывать графическую интерпретацию расчетов [1].

Одной из задач регрессионного анализа состоит в том, чтобы на основании ограниченного объёма экспериментальных данных (выборки) найти приближенное уравнение регрессии и оценить возникающую при этом ошибку. Однако найти обоснованную физическую модель, описывающую рассматриваемый процесс удается далеко не всегда. Иногда даже имеющаяся такая модель может оказаться слишком сложной и неудобной для практического использования [2].

Проведение регрессионного анализа с использованием пакета Microsoft Excel может быть осуществлено несколькими способами. Рассчитать коэффициенты однофакторного уравнения регрессии можно в процессе построения графика функции, воспользовавшись опцией «Добавить линию тренда» в контекстном меню рядов данных.

Решение задачи многофакторного регрессионного анализа можно провести с помощью Пакета анализа. Для этого необходимо оформить в виде блока ячеек значения вектора откликов у_э и матрицы независимых переменных X. Затем в пункте меню Сервис \ Анализ данных...\Регрессия заполнить соответствующие поля ввода для интервалов входной и выходной переменных и область для вывода результатов расчета [4].

Ниже рассмотрим применение перечисленных способов на примере. Был проведен эксперимент «Изучение влияния корреляции пласта на структурно-литологическое моделирование У (функция отклика) от независимого фактора Х величины запасов нефти в нём, представлены в виде таблицы на рабочем листе Excel (рис. 1).».

Таблица 1 - Данные для проведения однофакторного регрессионного анализа

Однофакторный регрессионный анализ с использованием линии тренда. Найдем подходящее уравнение регрессии для аппроксимации данной выборки непрерывной функцией. Построим график зависимости У от Х на основании выборки, выбрав тип диаграммы «Точечная» в Мастере диаграмм, что представлено на рисунке1.

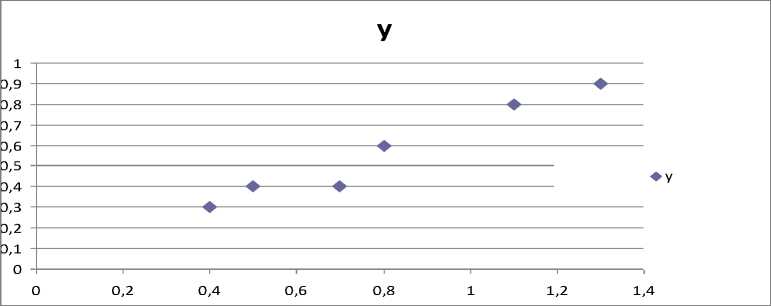
Рисунок 1 – График исходных данных

Добавим линию тренда. На вкладке «Тип» выберем вид уравнения регрессии, которым будут аппроксимированы выделенные данные. Выберем тип "Линейная", что соответствует уравнению однофакторной линейной регрессии. Как видно, линейное уравнение является не слишком хорошей аппроксимацией исходных данных, о чем свидетельствует также не достаточно близкое к единице значение R2 на рисунке 2.

Щёлкнем левой клавишей мыши на линии тренда с тем, чтобы выделить ее, в контекстном меню выберите пункт Формат линии тренда, и на вкладке «Тип» выберите тип «Полиномиальная», что соответствует уравнению регрессии в форме полинома.

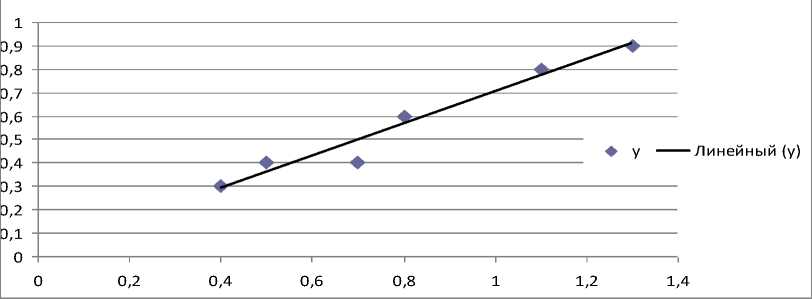
Рисунок 2 – График данных с аппроксимацией линейным уравнением регрессии

В поле «Степень» установите значение 2, что отвечает уравнению однофакторной параболической регрессии. После нажатия клавиши ОК программа автоматически перестроит линию тренда на диаграмме и выведет новое уравнение регрессии. Как видно из рисунка 3, аппроксимация исходных данных уравнением регрессии второй степени выглядит значительно лучше, о чем свидетельствует также близость к единице коэффициента достоверности аппроксимации. Повторим расчет, установив в поле «Степень» формы «Линия тренда» значение 5, что соответствует уравнению кубической регрессии, и убедимся, что в этом случае коэффициент достоверности аппроксимации становится равным единице.

Таким образом, полином пятой степени даёт наилучшую аппроксимацию исходных экспериментальных данных, и дальнейшее увеличение степени полинома, очевидно, не целесообразно.

Данные для регрессии: критерий R ², дисперсия адекватности и t-статистика отражены в таблицах 2,3 для проверки значимости коэффициентов.

Таблица 2 - Регрессионная статистика

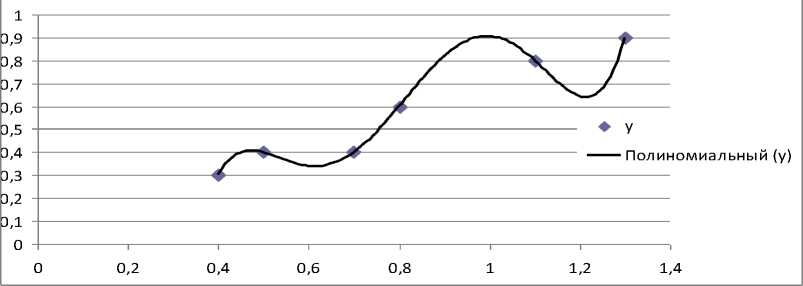
Рисунок 3 – График данных с аппроксимацией параболическим уравнением регрессии

Таблица 3 - Дисперсионный анализ

Отметим, что регрессионный анализ широко применялся и ранее.

Сейчас, когда ПК во многом освободил человечество от громоздких и порой вручную неосуществимых расчетов, применение такого анализа стало делом обыденным. Исследователю теперь остается грамотно спланировать сбор опытных данных, вывести результаты вычислений, уметь их анализировать и интерпретировать, а также оперативно изменять модель.