Применение информационных технологий при решении эконометрических задач

В настоящее время в процессе анализа текущей экономической ситуации возникает необходимость обрабатывать большой массив данных. Существует несколько программных продуктов, позволяющих совершать расчеты с использование методов математического анализа. В их числе общераспространённые содержащиеся в офисных пакетах MS Excel и OpenOffice. Для решения узкоспециализированных задач применяют эконометрические пакеты типа Statistica, Eviews, Stata, а также профессиональный кроссплатформенный пакет GRETL.

Среди основных этапов эконометрического исследования выделяют:

– постановки задачи;

– разработка теоретической модели;

– сбор данных;

– оценка параметров;

– апробация и интерпретация результатов;

– сопровождение модели.

Рассмотрим подробнее каждый из этих этапов и укажем основные проблемы, которые приходится решать при их реализации.

Задача № 1. Допустим необходимо определить зависимость выручки организации от производительности труда на одного человека (единицу) имея следующие данные (см. таблицу 1).

Порядковый номер

Производительность труда (единицу)

Выручка (тыс. руб.)

Табл. 1. Данные по предприятию

Для решения текущей задачи необходимо провести следующие операции:

• 1.    Построить линейное уравнение парной регрессии.

• 2.    Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

• 3.    Оценить статистическую значимость параметров регрессии и корреляции (критерий Стьюдента).

• 4.    Дать точечный и интервальный прогноз прибыли с вероятностью 0,95, принимая уровень выработки равным 92 единицам[1].

Используя специализированное программное обеспечение можно определить следующие параметры: уравнения линейной регрессии y=a+bx, линейный коэффициент корреляции с проверкой его значимости; тесноту связи с помощью показателей корреляции и детерминации, МНК-оценку, статическую надежность регрессионного моделирования с помощью F-критерия Фишера и с помощью t-критерия Стьюдента, доверительный интервал прогноза для уровня значимости α.

Для нахождения параметров регрессии используется метод наименьших квадратов. На практике данная процедура осуществляется посредством использования матричного метода в MS Excel.

Метод наименьших квадратов представляет собой математическую процедуру составления линейного уравнения, максимально соответствующего набору упорядоченных пар, путем нахождения значений для a и b, коэффициентов в уравнении прямой (рис. 1)[2]. Цель метода наименьших квадратов состоит в минимизации общей квадратичной ошибки между значениями y и ŷ. Если для каждой точки мы определяем ошибку ŷ, метод наименьших квадратов минимизирует:

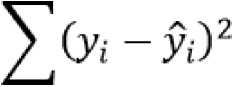
1 = 1

Рис. 1. Формула метода наименьших квадратов где n = число упорядоченных пар вокруг линии максимально соответствующей данным. Пример математического моделирования данного уравнения представлено на рисунке 2.

На рисунке 2 показано что линия, максимально соответствующая данным, линия регрессии, минимизирует общую квадратичную ошибку четырех точек на графике.

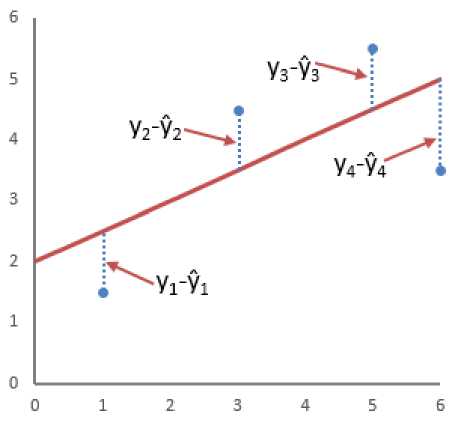
Рис. 2. Визуальное моделирование метода наименьших квадратов

В случае необходимости построения парной регрессионной модели необходимо изобразить регрессионную зависимость графически [3]. Парная регрессия представляет собой регрессию между двумя переменными - у и x, т. е. модель вида: y(x) = Г(х), где у - зависимая переменная (результативный признак); x - независимая, или объясняющая, переменная (признак-фактор). Знак «л» означает, что между переменными x и у нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина укладывается из двух слагаемых: y = yx + е, где у - фактическое значение результативного признака;  yx - теоретическое значение результативного признака, найденное исходя из уравнения регрессии; е - случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Графически покажем регрессионную зависимость между выработкой продукции на одного работника и удельного веса рабочих высокой квалификации (см. рисунок 3).

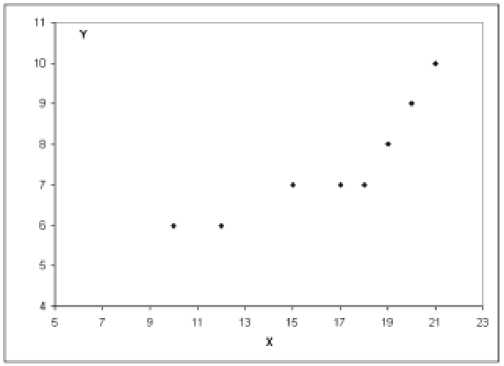
Рис. 3. Визуальное моделирование парной регрессии

В данной статье мы привели пример использования специализированного программного продукта при решении экономической задачи. В данном случае мы использовали регрессионную модель второго порядка и центральный композиционный план.

Таким образом, отметим, что применение информационных технологий в решении эконометрических задач позволяет не только ускорить время работы с большим массивом данных, но и представить наглядно состояние и тенденции изучаемой экономической ситуации.