Применение интеграла в экономике

Современный экономист должен хорошо владеть количественными методами анализа. Такой вывод нетрудно сделать практически с самого начала изучения экономической теории. В тоже время, знания традиционных математических курсов (математический анализ, линейная алгебра, теория вероятностей), так и знания, необходимые непосредственно в практической экономике и экономических исследованиях (математическая и экономическая статистика, теория игр, эконометрика и др.) важны [2].

Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и точной формулировки экономических понятий и проблем.

Традиционно практическое приложение интеграла иллюстрируется вычислением площадей различных фигур, нахождением объемов геометрических тел и некоторыми приложениями в физике и технике. Однако роль интеграла в моделировании экономических процессов не рассматривается. Часто экономические приложения интеграла не обсуждаются в классах экономического направления. В тоже время, интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в экономике [3].

Интеграл (от лат. Ц понятий математики, возникшее в связи с необходимостью, с одной стороны, найти функции по их производным (например, найти функцию, выражающую путь, пройденный движущейся точкой, скорость этой точки), а с другой-измерить площадь, объем, длину дуг, работу сил за определенный промежуток времени и т.д. [4].

Символ введен Лейбницем (1675). Этот символ является изменением латинской буквы S (первой буквы слова сумма). Слово Интеграл придумал Я. Бернулли (1690). Вероятно, оно происходит от латинского integero, что переводится как довести до предыдущего состояния, восстановить.

В ходе переписки И. Бернулли и Г. Лейбниц согласились с предложением И. Бернулли. Тогда же, в 1696г., появилось и название новой отрасли математики integral интегральное исчисление (calculus integralis), которое ввел И. Бернулли [3].

Во-первых, рассмотрим концепцию потребительских издержек в рыночной экономике. Итак, рассмотрим некоторые экономические понятия и обозначения [1].

Спрос на данный товар представляет собой текущую зависимость между объемом покупки и ценой товара в определенный момент времени. Графически спрос на отдельный продукт изображается в виде отрицательной кривой наклона, отражающей соотношение между количеством продукта Q и ценой P единицы этого продукта и которую потребители готовы купить по каждой данной цене. Отрицательный наклон кривой спроса имеет следующее объяснение: чем дороже товар, тем меньше количество товара, которое готовы купить покупатели, и наоборот [1].

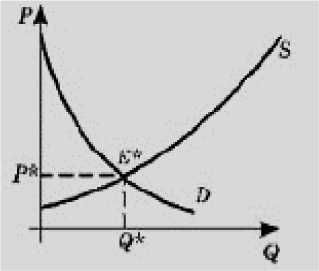
Рассмотрим понятие, которое играет важную роль в моделировании экономических процессов - рыночное равновесие. Равновесное состояние характеризуется: количеством и ценой, при которой объем спроса совпадает с величиной предложения, а графически это представлено точкой пересечения кривых спроса и предложения [5].

Далее, для удобства анализа, мы начнем рассматривать обратные функции спроса и предложения, которые характеризуют зависимость P-KQ) , а не зависимость e-z^ .

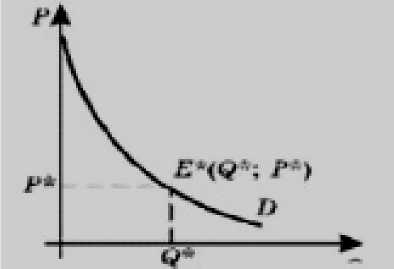
Теперь,        чтобы       определить потребительские     излишек,     рассмотрим приложения интегрального анализа. Для этого на графике показана функция обратного спроса P-Z^t . Предположим, в точке F(,CT,P"\ установилось рыночное равновесие (для удобства дальнейшего анализа на графике нет кривой предложения) [5].

Если покупатель по равновесной цене P*, приобретает товар в количестве Q*, то, следовательно, что расходы общие на покупку такого товара составят P*Q*, и это на графике соответствует площади заштрихованной фигуры A [5].

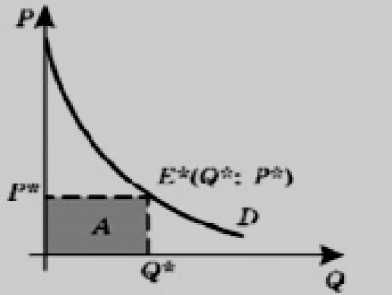
Но представьте, что товар в количестве Q* продавцы продают не сразу, а небольшими партиями Q поступает на рынок. То есть такое допущение, наряду с непрерывностью функции спроса и предложения при выводе формулы, является основным для расчета потребительских излишек.

Расчетом потребительских излишек является разница между максимальной суммой денег, которую потребитель желает и готов платить за купленное количество благ, и суммой денег, которую он фактически заплатил за товар.

Таким образом, потребительские издержки могут быть рассчитаны по следующей формуле [1]:

1                                                  (1)

Рассмотрим задачу на определение излишка потребителя.

Пусть известно, что на некоторый товар спрос задается функцией B-*-q' , где q – количество товара (в шт.), p – цена единицы товара (в руб.), а при /-f-1достигается равновесие на рынке данного товара. Необходимо определить величину потребительского излишка [1].

Решение.

CbVr>(3№_,V_L-^№-Ll-{4?-^                  z

1            1                                            (2) (руб.).

Рассмотрим оценку последствий введения потоварного налога.

В предложении, где существует единственная возможность производства продукта, введение потоварного налога приводит к нужному результату, и при этом объем выпуска и размер внешнего эффекта, несомненно, связаны друг с другом.

После введения потоварного налога уменьшается объем как потребления, так и производства. Помимо этого, более высокую цену платят покупатели, а более низкую получают относительно первоначальной равновесной цене. Поэтому, налог ухудшает экономическое положение и продавцов, и покупателей.

Дана кривая спроса s-io-i? . Каковы денежные затраты потребителя при введении налога на данный товар с единицы продаж в размере 1 руб., когда известно, что при цене Г-2 руб. наблюдалось первоначальное рыночное равновесие на этом рынке [1].

Таким образом, рассмотренный способ решения широко применяется на практике. Экономисты вычисляют в зависимости от различных вариантов налогообложения изменения потребительских излишков, и с учетом необходимого размера налоговых поступлений анализируют полученные результаты, останавливаются на тех вариантах, которые вызывают наименьшее сокращение потребительских выгод.