Применение искусственных нейронных сетей для моделирования нестационарных аэродинамических характеристик

Существенное расширение диапазона реализуемых в полете углов атаки современных самолетов приводит к необходимости более точного моделирования их нестационарных аэродинамических характеристик в условиях возможного срыва потока. Это касается как маневренных самолетов с крылом малого удлинения и большой стреловидности, вследствие использования динамических выходов на сверхбольшие углы атаки в современном воздушном бою, так и самолетов с крылом большого удлинения, которые вследствие желаемого сокращения взлетной дистанции и увеличения веса взлетают и садятся на больших углах атаки, а возможные ветровые порывы могут приводить к развитию динамического отрыва потока.

Для самолетов с крылом малого удлинения определяющим физическим эффектом на больших углах атаки является разрушение вихрей, сходящих с наплывов крыла и носовой части фюзеляжа. Именно движение координаты разрушения вихрей с изменением углов атаки и скольжения в стационарных условиях приводит к нелинейным изменениям коэффициентов аэродинамических характеристик и производных устойчивости и управляемости самолета. Если в стационарных условиях эти явления изучены достаточно хорошо и им посвящена обширная литература, то в нестационарных условиях эти явления еще далеки от детального понимания. Именно учет нестационарных эффектов особенно важен для практики, потому что в диапазоне больших углов атаки самолеты, как правило, не летают на установившихся режимах, а попадают туда вследствие динамических маневров или развития критических режимов полета.

В настоящее время в инженерных приложениях при исследованиях динамики полета широко используется представление аэродинамических коэффициентов с помощью концепции аэродинамических производных. Расширение применения данного метода на условия полета с большими углами атаки происходит за счет добавления нелинейных зависимостей от угла атаки, полученных в аэродинамической трубе. Вместе с тем данный подход не дает необходимой точности результатов на больших углах атаки из-за существенных динамических эффектов, вызванных динамикой отрыва потока и разрушения вихрей. На этих режимах обтекания аэродинамические производные, как показывает эксперимент [1, 2], зависят от частоты и амплитуды колебаний, что

ТРУДЫ МФТИ. — 2011. — Том 3, № 3 Аэрокосмические исследования, прикладная механика 65 делает моделирование аэродинамических коэффициентов на основе данного подхода невозможным.

В общем случае при моделировании аэродинамических коэффициентов необходимо учитывать предысторию движения. Это условие является особенно важным в случае наличия срывов потока и/или разрушений вихрей, что вызывает существенные для динамики твердого тела явления с некоторым запаздыванием по времени.

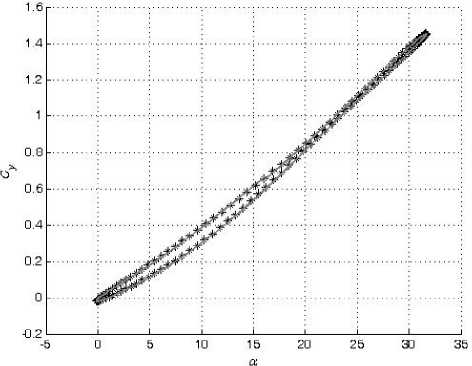
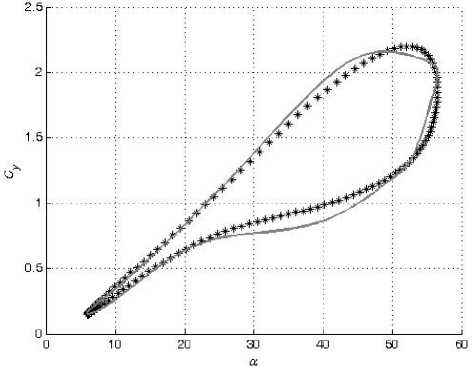
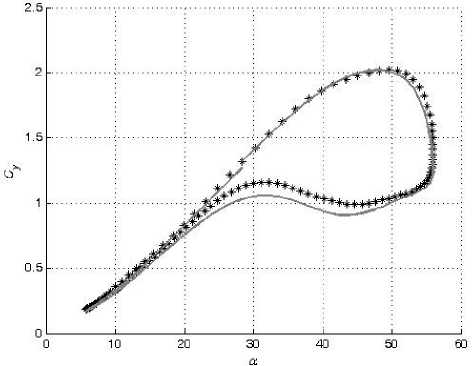
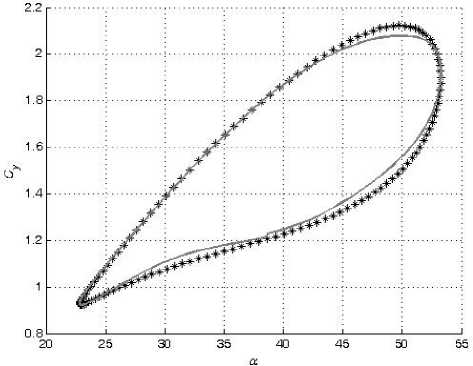
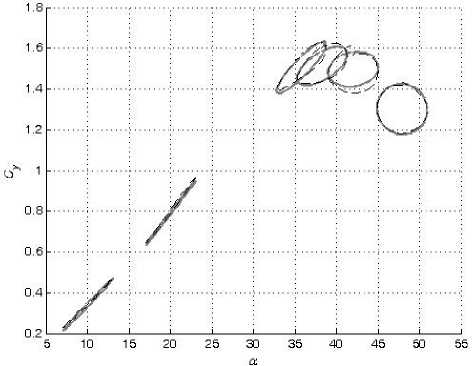
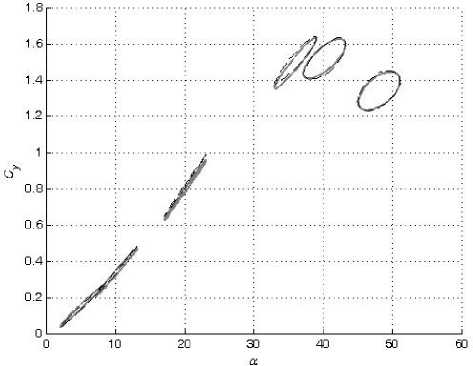
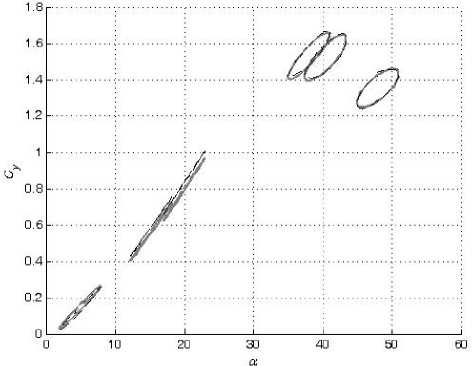
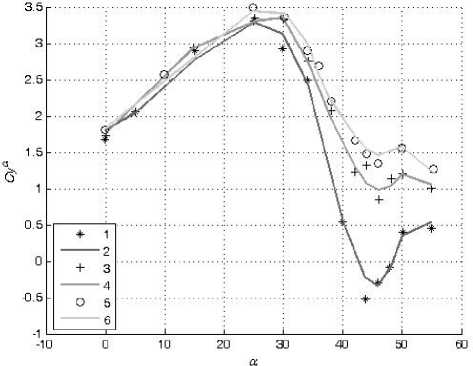
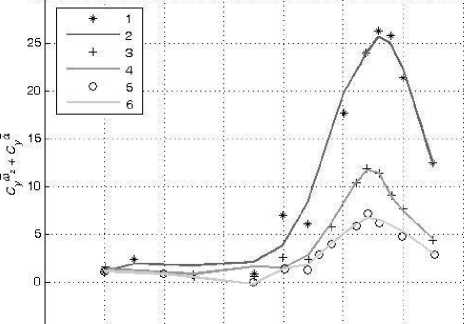
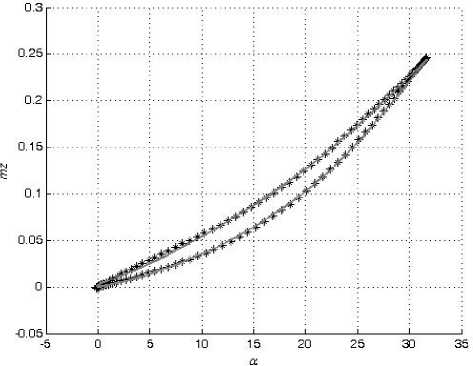
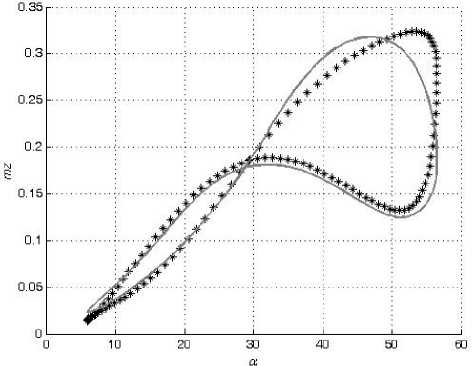
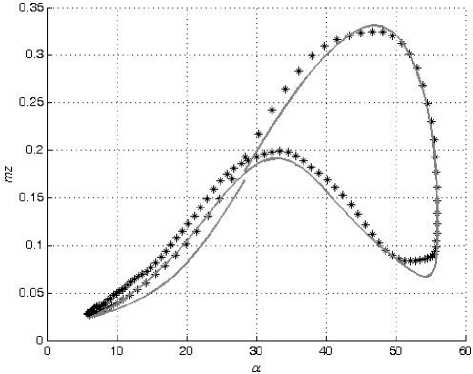
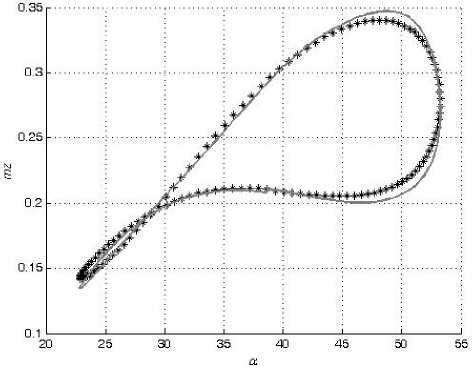
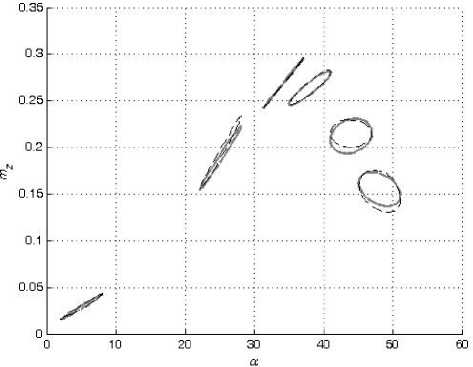
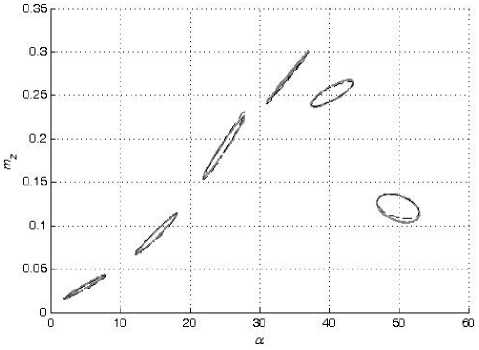
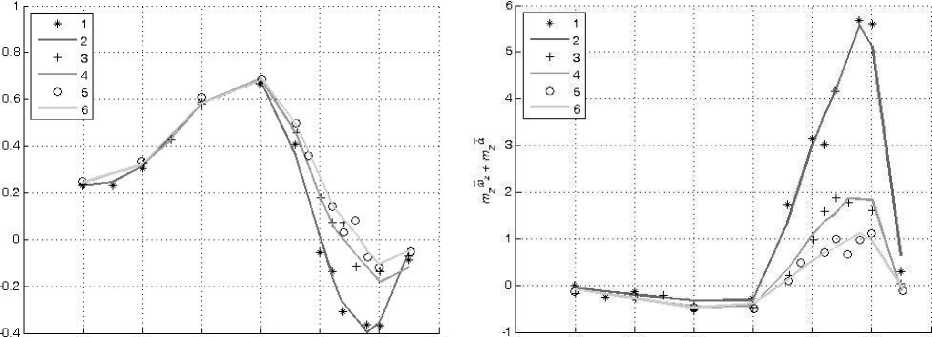
В настоящей работе смоделированы зависимости коэффициентов подъемной силы C y и вращательного момента m z от угла атаки α в широком диапазоне амплитуд колебаний модели треугольного крыла по углу атаки с помощью искусственных нейронных сетей. Кроме тог о , также смоделированы значения их производных C _y ^α и m _z ^α , комплексов производных C _y ^{ω z} + C _y ^α и m _z ^{ω z} + m _z ^{α z} . Для обучения и проверки способности нейронной сети к обобщению были использованы экспериментальные данные, полученные в работе [2].

Для моделирования C _y и m _z использовались две отдельные нейронные сети, одним из требований к которым при разработке было наличие хорошей обобщающей способности, то есть способности нейронной сети моделировать с удовлетворительной точностью значения аэродинамических характеристик, которые не использовались при её обучении.

• II.    Существующие методы математического моделирования нестационарных аэродинамических характеристик

Использование нелинейных переходных функций является наиболее общим методом моделирования нестационарных аэродинамических характеристик [4]. Разработка и проверка модели на основе нелинейных переходных функций требует огромного объема нестационарных аэродинамических данных, поэтому для практических целей метод нелинейных переходных функций представляет значительные трудности. Он требует специальных методов определения нелинейных переходных функций и организации их функциональной аппроксимации. Конечная математическая модель динамики полета при этом формулируется в классе интегро-дифференциальных уравнений, что ведет к существенному усложнению моделирования динамики, исследования устойчивости и синтеза управления.

Феноменологический подход, основанный на моделировании внутренней динамики течения, применен в [5, 6, 7]. При данном подходе используются переменные внутреннего состояния или аэродинамические нагрузки разделяются на статические (не запаздывающие) и динамические составляющие. Нестационарные аэродинамические характеристики описываются при помощи нелинейных дифференциальных уравнений. Данные уравнения содержат характерные временные постоянные, соответствующие временам установления отрывного обтекания и/или разрушения вихрей. Эти константы определяются с помощью экспериментов с моделью в аэродинамической трубе. Данный подход позволяет моделировать достаточно точно как зависимость аэродинамических производных от частоты, так и аэродинамические реакции при больших амплитудах и возможный аэродинамический гистерезис. Вместе с тем применение данных методов имеет свои ограничения [8], в частности, при определении аэродинамических характеристик произвольного летательного аппарата.

• III.    Применение искусственных нейронных сетей для моделирования нестационарных аэродинамических характеристик

Альтернативным подходом является моделирование аэродинамических характеристик с применением искусственных нейронных сетей. Использование данного математического аппарата имеет ряд преимуществ. Так, например, известно [9], что любая непрерывная функция многих переменных может быть аппроксимирована с помощью нейронной сети с любой заданной точностью. Кроме того, преимущество данного метода заключается в гибкости его применения, так как не требуются значительные упрощающие предположения, что позволяет моделировать характеристики летательных аппаратов произвольной сложности [10, 11, 12].

Искусственную нейронную сеть можно рассматривать как направленный граф со взвешенными связями, в котором узлами являются некоторые элементарные процессоры, называемые искусственными нейронами [13]. Нейрон к получает «входные сигналы» (e i ) i =i ,n от других нейронов или входных узлов нейронной сети. Получив набор сигналов, нейрон умножает каждый сигнал на весовой коэффициент w _ik , соответствующий данному входу, и суммирует полученные произведения. Результат суммирования подвергается нелинейному преобразованию посредством функции активации нейрона f _k .

Выражение, связывающее между собой вход (e i ) i =i ,n и выход У к нейрона, представляется в следующем виде:

У к = f k (^ W ik e i + ° к ).                                   (1)

i

Веса связей w ik и порог θ k определяются в ходе «обучения» нейронной сети с помощью минимизации разницы между выходом из сети и данными, задаваемыми в качестве цели обучения.

Среди всего многообразия нейронных сетей одним из наиболее распространенных типов является многослойный персептрон. Нейронные сети данного типа обычно состоят из входного слоя, на который подаются входные сигналы, одного или нескольких скрытых слоев, в которых происходит обработка входного сигнала, и выходного слоя, с которого считываются результаты работы сети.

• IV.    Математическая модель нестационарных аэродинамических характеристик треугольного крыла

Для малых амплитуд колебаний модели в потоке может быть использовано следующее разложение аэродинамических коэффициентов C _y и m _z [3]:

C y = C y _CT ^{( a} 0 ) ⁺ C ^{a ( a — a} 0 ) + ⁽C ^a + C y z ^{) a                         (2)}

и mz = mzCT (ao) + ma • (a - ao) + (maz + mT )a.                      (3)

Вместе с тем такое представление аэродинамических коэффициентов не может быть использовано для их моделирования при движении, сопровождающемся большими амплитудами изменения угла атаки.

Таким образом, при проведении экспериментальных исследований треугольного крыла [2] были проведены три типа опытов — статический, динамический при колебании модели с малыми амплитудами и динамический при колебании модели с большими амплитудами. В ходе проведения первых испытаний проводилось измерение статических значений С у ст (a o ) и m z _CT (a o ), при проведении вторых — значений динамичес к их производных аэродинамических коэффициентов C ^a , m a и комплексов производных C ^ z + C ^a и m ^ z + m a z • В ходе же проведения испытаний при колебании модели с большими амплитудами проводилось измерение нелинейных нестационарных зависимостей C y (t) и m z (t).

При проведении экспериментов была использована модель треугольного крыла удлинением А = 1,5, имеющего среднюю аэродинамическую хорду (САХ) b a = 0,725 м, стреловидность крыла X « 70 ° .

Исследования проводились в аэродинамической трубе Т-103 ЦАГИ при скорости потока V ^ = 25 м/с, что соответствует числу Рейнольдса Re = 1,2 • 10 ⁶ , рассчитанному по САХ крыла.

При проведении динамических испытаний колебания проводились по закону a = ao + Aa sin(wt + у).                                 (4)

Колебания с малыми амплитудами выполнены для трех частот: f = 2 П 0.5, 1 и 1.4 Гц. Амплитуда колебаний A a составляла 3 ° . Средние углы a o менялись от 0 ° до 60 ° .

При колебаниях с большой амплитудой частота f менялась от 0,2 Гц до 1,2 Гц. Амплитуда колебаний Aa менялась от 15 ° до 24 ° . Средние углы атаки a o составляли от 16 ° до 32 ° . За один период измерялось по 128 значений C _y и m _z при соответствующих им углах α.

С помощью полученных производных С^:, m a и комплексов производных C ^ z +C ^a и m ZZ z +m a z , а также значений коэффициентов в стационарном случае С у ст (а о ) и m _{Z cT} (а д ) на основе (2) и (3) были восстановлены значения С у (t) и m _z (t) при колебании модели с малыми амплитудами.

С помощью указанного метода были сгенерированы данные для обучения и тестирования нейронных сетей для случая колебаний с малыми амплитудами по 64 значения за период. Количество измерений за период было уменьшено по сравнению с колебаниями с большими амплитудами, поскольку кривые гистерезиса, возникающие при больших амплитудах, имеют более сложный характер. При обучении сетей использовались как данные, полученные в ходе проведения испытаний при колебаниях модели с большими амплитудами, так и данные, восстановленные для колебаний модели с малыми амплитудами. В общей сложности при обучении нейронной сети было использовано 44 теста, 8 из которых — при большой амплитуде, а 36 — при малой. Для проверки обобщающей способности нейронной сети всего было использовано 22 теста, из них 4 теста при большой амплитуде и 18 тестов при малой амплитуде.

На вход нейронной сети подавался вектор входных данных

I = (t,a(t),

Для моделирования C_y и m_z были использованы две нейронные сети типа многослойный персептрон, каждая с двумя скрытыми слоями, общее число нейронов составило 20 и 18 соответственно. Обучение проводилось методом обратного распространения. В качестве функции активации нейрона была выбрана сигмоидная функция f = ^-x. В качестве алгоритма минимизации использовался алгоритм Левенберга–Маркара. Моделирование проводилось с помощью специализированного пакета в среде MATLAB.

При выборе тестов, включаемых в обучающее множество, предпочтение отдавалось тем тестам, в которых происходило наибольшее изменение вторых производных Cy , m_z по α, производной комплексов производных С^ z + Су⁸ и m^z + ma по а или самих значений производных.

Порядок точности аппроксимации данных нейронной сетью в каждом отдельном случае был искусственно ограничен, так как дальнейшее увеличение точности аппроксимации приводило к ухудшению обобщающей способности.

Рис. 1. Зависимость Cy от а, амплитуда 16°, f = 0. 813 Гц, средний угол атаки а = 16°, полученная экспериментально (маркер *) и смоделированная нейронной сетью (сплошная линия)

Рис. 2. Зависимость Cy от а, амплитуда 24°, f = 0. 80 Гц, средний угол атаки а = 32°, полученная экспериментально (маркер *) и смоделированная нейронной сетью (сплошная линия)

Результаты. На рис. 1, 2, 3, 4 представлены результаты моделирования коэффициента Cy нейронной сетью при колебаниях треугольного крыла с большими амплитудами, а также сравнение с данными эксперимента [2]. Необходимо отметить, что на рис. 1 представлен график, принадлежащий обучающему множеству, тогда как на рис. 2--4 представлены результаты, не принадлежащие обучающему множеству.

Рис. 3. Зависимость Cy от а, амплитуда 24°, f = 0. 25 Гц, средний угол атаки а = 32°, полученная экспериментально (маркер *) и смоделированная нейронной сетью (сплошная линия)

Рис. 4. Зависимость Cy от а, амплитуда 15°, f = 0. 81 Гц, средний угол атаки а = 38°, полученная экспериментально (маркер *) и смоделированная нейронной сетью (сплошная линия)

Рис. 5. Зависимость Cy от а, амплитуда 3°, f = 0. 5 Гц, полученная экспериментально (сплошная линия) и смоделированная нейронной сетью (пунктирная линия)

Рис. 6. Зависимость Cy от а, амплитуда 3°, f = 1 Гц, полученная экспериментально (сплошная линия) и смоделированная нейронной сетью (пунктирная линия)

Рис. 7. Зависимость Cy от а, амплитуда 3°, f = 1,4 Гц, полученная экспериментально (сплошная линия) и смоделированная нейронной сетью (пунктирная линия)

Рис. 8. Зависимости C_y^α, полученные для частот 0.5, 1, 1. 4 Гц в эксперименте — 1, 3, 5, смоделированные нейронной сетью — 2, 4, 6

-5

•10 О 10 20 X 40 50 60

Рис. 9. Зависимости C_y^ωz+ C_y^α, полученные для частот 0.5, 1, 1. 4 Гц в эксперименте — 1, 3, 5, смоделированные нейронной сетью — 2, 4, 6

Рис. 10. Зависимость mz от а, амплитуда 16°, f = 0. 813 Гц, полученная экспериментально (маркер *) и смоделированная нейронной сетью (сплошная линия)

Рис. 11. Зависимость mz от а, амплитуда 24°, f = 0. 80 Гц, полученная экспериментально (маркер *) и смоделированная нейронной сетью (сплошная линия)

Рис. 12. Зависимость mz от а, амплитуда 24°, f = 0. 25 Гц, полученная экспериментально (маркер *) и смоделированная нейронной сетью (сплошная линия)

Рис. 13. Зависимость mz от а, амплитуда 15°, f = 0. 81 Гц, полученная экспериментально (маркер *) и смоделированная нейронной сетью (сплошная линия)

10    15    20    25 X 35    40    45    50    55

Рис. 14. Зависимость mz от а, амплитуда 3°, f = 0. 5 Гц, полученная экспериментально (сплошная линия) и смоделированная нейронной сетью (пунктирная линия)

Рис. 15. Зависимость mz от а, амплитуда 3°, f = 1 Гц, полученная экспериментально (сплошная линия) и смоделированная нейронной сетью (пунктирная линия)

Рис. 16. Зависимость mz от а, амплитуда 3°, f = 1. 4 Гц, полученная экспериментально (сплошная линия) и смоделированная нейронной сетью (пунктирная линия)

•10        0        10       20       30       40       50       60         -10        0        10       20       30       40       50       60

а                                                        а

Рис. 17. Зависимости та, полученные для частот Рис. 18. Зависимости m“z + ma, полученные для 0.5, 1, 1. 4 Гц в эксперименте — 1, 3, 5, смоделиро- частот 0.5, 1, 1. 4 Гц в эксперименте — 1, 3, 5, ванные нейронной сетью — 2, 4, 6 смоделированные нейронной сетью — 2, 4, 6

Результат моделирования для опыта, принадлежащего обучающему множеству, лучше, чем результаты, полученные для данных, не включенных в обучающее множество. Данный факт можно объяснить тем, что в первом случае нейронная сеть используется для аппроксимации зависимостей, то есть для «восстановления» ранее «выученных» результатов, тогда как во втором случае происходит обобщение полученных «знаний» на ту область, в которой обучение не проводилось.

Из результатов моделирования видно, что при колебаниях крыла с большими амплитудами наблюдается гистерезис, который неплохо описывается разработанной нейронной сетью.

На рис. 5, 6, 7 представлены результаты моделирования Cy нейронной сетью при колебаниях модели с малыми амплитудами угла атаки на тех данных, которые не использовались при обучении модели.

Как видно из графиков, модель и в случае вынужденных колебаний с малой амплитудой неплохо описывает данные экспериментов. Несмотря на то, что основной задачей является моделирование аэродинамических коэффициентов при колебаниях модели с большими амплитудами, модель может быть использована также и для моделирования колебаний с малыми амплитудами.

Также в работе исследовалась способность нейронной сети моделировать зависимость производных Cya, C^z + Cya от частоты колебания модели. Результаты моделирования, а также данные эксперимента представлены на графиках (рис. 8, 9). Из графиков видно, что при колебаниях

ТРУДЫ МФТИ. — 2011. — Том 3, № 3 Аэрокосмические исследования, прикладная механика 71 модели с различными частотами наблюдается расщепление производных по этим частотам. Использование нейронной сети позволяет моделировать данное расщепление с неплохой точностью.

На рис. 10, 11, 12, 13 представлены результаты моделирования mz для больших амплитуд колебаний, рис. 14, 15, 16 — для малых амплитуд колебаний, а также сравнение с экспериментом. Для больших амплитуд колебаний можно также отметить наличие гистерезиса mz, который, как и в случае с Cy, хорошо моделируется нейронной сетью.

Также было произведено моделирование производной та и комплекса производных m^z + ma от а для разных частот. Сравнение полученных зависимостей с экспериментом приведено на рис. 17, 18. Из графиков видно, что в области а > 30° наблюдается расщепление значений производных в зависимости от частоты колебаний модели, которое удовлетворительно моделируется нейронной сетью.

• V.    Выводы

Представлена возможность использования искусственных сетей для моделирования аэродинамических характеристик в широком диапазоне углов атаки в случае гармонических колебаний на примере треугольного крыла. Разработанная математическая модель описывает результаты динамических экспериментов с вынужденными колебаниями малой амплитуды, полученных при различных частотах. Та же модель адекватно описывает результаты динамических испытаний с большими амплитудами для разных частот колебаний модели. Показано удовлетворительное согласование результатов этого моделирования с данными экспериментов. В дальнейшем планируется расширить предложенный подход на случай произвольного движения летательного аппарата, а также на случай компоновки реального самолета.