Применение экспериментально-расчетного подхода для идентификации деформационных и прочностных характеристик упругопластических материалов при квазистатическом и динамическом нагружениях

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2025PNRPU MECHANICS BULLETIN

На сегодняшний день известен широкий набор математических моделей нелинейного деформирования и разрушения упругопластических материалов при квази-статическом и динамическом нагружении. Для применения этих моделей требуются достоверные истинные диаграммы деформирования упругопластических материалов вплоть до разрушения образцов. Получить истинные диаграммы деформирования с помощью экспериментальных измерений крайне сложно, так как при испытаниях лабораторные образцы подвергаются неодноосному и неоднородному напряженно-деформированному состоянию (НДС), а также существенному влиянию краевого эффекта, сил трения и радиальной инерции в экспериментах на растяжение и ударное сжатие. Обычно определение деформационных характеристик материала выполняется с использованием экспериментально-аналитических методик [1–16], которые основаны на упрощающих гипотезах. Эти методы не позволяют в полной мере учесть при больших деформациях неодноосность и неоднородность НДС в экспериментах как на растяжение, так и на сжатие компактных образцов при квазиста-тических и динамических нагружениях. В связи с этим для определения и исследования деформационных и прочностных свойств материалов актуально развитие экспериментально-расчетного подхода [17–22], позволяющего, в отличие от экспериментально-аналитических методов, без принятия упрощающих гипотез учесть неодноосность и неоднородность НДС. На основе экспериментально-расчетного подхода [17] авторами были разработаны методики и алгоритмы исследования деформационных и прочностных характеристик упругопластических материалов при различных видах нагружения [18–22].

Из анализа современных работ [23–25] по моделированию процессов разрушения можно сделать вывод, что на сегодняшний момент не существует универсального подхода или модели, описывающей процессы разрушения в полном объеме. Исходя из многообразия факторов и причин разрушения материалов, вместо создания громоздких моделей, описывающих все известные на сегодняшний день эффекты на основе единых кинетических уравнений, более целесообразным является создание некоторой составной модели поврежденного материала, состоящей из более простых, формально независимых моделей. Предлагается связанная модель разрушения на основе кинетического уравнения накопления поврежде- ний в сочетании с критерием прочности типа Писаренко – Лебедева. Данный критерий разрабатывался для описания предельных состояний именно квазихрупких материалов, но в дальнейшем успешно использовался и для пластичных материалов. При этом критерий позволяет учитывать особенности свойств материала и его склонность к последовательному разрушению отрывом и сдвигом.

В рамках развития экспериментально-расчетного подхода разработана методика идентификации материальных параметров предложенной модели разрушения. Этот подход предполагает проведение совместного анализа результатов эксперимента и полномасштабного (в рамках механики сплошных сред) компьютерного моделирования процессов деформирования лабораторных образцов или элементов конструкций без принятия априорных силовых и кинематических гипотез. Представляется возможным строить предельную поверхность разрушения в зависимости от вида НДС, определенного в численных расчетах на момент разрушения. Высокая информативность и точность получения деформационных и прочностных характеристик материалов позволят повысить уровень достоверности диагностики состояния и прочности элементов конструкций, находящихся в условиях эксплуатации.

Экспериментально-расчетный подход

В общем случае для определения механических констант и определения диаграммы деформирования материала формируется целевая функция, описывающая различия натурных и численных экспериментов. Далее строится итерационный процесс нахождения механических констант и зависимостей материала.

Требуется найти набор параметров уравнения состояния b = ( b 1 , b 2 ,...., b n ) , при которых численное решение задачи наилучшим образом согласуется с результатами эксперимента . Здесь параметрами могут выступать мо дуль объемного сжатия K, модуль сдвига G, предел те кучести σ _Т , интенсивности напряжений при фиксиро ванном значении накопленных пластических деформа ций О i (ж) и др. Для определения искомых параметров требуется минимизировать функцию , представляющую собой величину среднеквадратичного отклонения рас четных и экспериментальных результатов :

N ₂

C ⁽ b ) = Ё ( Р Э - p j ) , j = 1

Э где pЭj – значение параметров сравнения, полученных из

Р эксперимента, pj – значение параметров сравнения, полученных из расчета. Параметрами сравнения могут быть силы, перемещения, напряжения, деформации и др. В качестве ограничений на искомые параметры bi в области поиска выступают уравнения начально-краевой задачи, а границы области поиска определяются из экспериментальных фактов и физических принципов. Решение рассмотренной задачи во многом зависит от выбора алгоритма оптимизации. При выборе существующих и создании новых алгоритмов необходимо учитывать особенности рассматриваемых задач. В рассматриваемом случае проверка ограничений осуществляется путем численного решения нелинейной начально-краевой задачи, что требует больших вычислительных затрат. Поэтому большую роль играет время счета одного варианта, выбор начального приближения и скорость сходимости вычислительного процесса. Целесообразно общую задачу сводить к последовательности частных задач с одним-двумя параметрами сравнения. Начальное приближение определяется аналитическим или численным решением идеализированной задачи. В качестве алгоритма оптимизации можно использовать метод последовательных приближений искомых параметров, основанный на коррекции параметров, исходя из относительного отличия экспериментальных и расчетных значений.

Построение истинных диаграмм деформирования упругопластических материалов при квазистатическом и динамическом нагружениях

Наиболее распространенными способами изучения и исследования деформационных характеристик упруго пластических материалов при квазистатическом и дина мическом нагружениях являются эксперименты на растя жение сплошных стержней и сжатие компактных образ цов . На основе экспериментально - расчетного подхода разработаны методики [17–22] построения квазистатиче - ских и динамических истинных диаграмм деформирова ния при больших деформациях и неоднородном НДС .

В экспериментах на растяжение построение истинных диаграмм деформирования материалов осуществляется в результате итерационной процедуры корректировки зависимости интенсивности напряжений σi от параметра Одквиста æ на всем процессе деформирования образца. Для этого в каждой итерации численного решения задачи растяжения образца анализируется отношение значений осевых сил, полученных в эксперименте FЭ и расчете Fp при одинаковом удлинении образца: в = F3 / FP ■ Затем устанавливается функциональная зависимость между максимальным значением параметра Одквиста в объеме образца ж* и соответствующим удлинением. Итерационная процедура корректировки диаграммы осуществляется по формуле О i (ж*) = во i (ж*) до совпадения с заданной точностью зависимостей осевых сил, полученных в эксперименте и расчете. Корректировка производится сразу всей диаграммы деформирования. В связи с этим необходимо многократно решать прямую задачу и выполнять соответствующую обработку ее результатов, что является весьма трудоемким вычислительным процессом. Данный алгоритм позволяет воспользоваться любой доступной программой решения прямой задачи без каких-либо модификаций. Как показали исследования, для сходимости итерационной процедуры достаточно в качестве начального приближения задать любую выпуклую диаграмму деформирования упрочняющегося материала. На рис. 1 схематично представлена процедура методики построения истинных диаграмм деформирования при растяжении.

Для повышения эффективности методики целесообразно осуществить процедуру нелинейной экстраполяции [22]. Вычислительный процесс, моделирующий нагружение, разбивается на этапы. Количество этапов равно количеству точек в табличном представлении экспериментальной зависимости осевой силы от осевого удлинения, и столько же точек будет содержать построенная истинная диаграмма деформирования. В ходе вычислений в конце каждого этапа анализируется величина отклонения расчетной осевой силы от экспериментальной. При превышении ею заданного значения производится аналогичная итерационная корректировка истинной диаграммы деформирования. Для продолжения прямого расчета на следующем интервале разбиения применяется процедура нелинейной экстраполяции диаграммы деформирования. Процесс построения диаграммы деформирования практически сводится к однократному прямому численному расчету без применения итерационной процедуры, что существенно повышает эффективность методики (до 10 раз). При этом предложенная методика реализована в виде отдельного консольного приложения с использованием языка программирования C++ в операционной системе Windows 10, что также значительно снижает вычислительные затраты на построение истинных диаграмм деформирования.

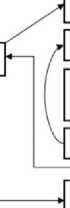
В экспериментах на сжатие компактных образцов определение динамических диаграмм деформирования и сил трения основывается на следующей итерационной методике. Первоначально диаграммы деформирования строятся по экспериментальной осевой силе при коэффициенте трения, равным нулю при однородном напряженно-деформированном состоянии. Затем осуществляется итерационный процесс определения коэффициентов трения с найденной диаграммой деформирования. В процессе итераций корректируются коэффициенты трения на нижней и верхней поверхностях образцов-таблеток посредством линейной интерполяции (экстраполяции) по разности высот арок в расчете и эксперименте до сходимости. Высоты полуарок определяются по формуле h = Rmax - R*, где R* = RН или R* = RВ , Rmax – максимальный радиус деформированного образца, RН, RВ – минимальные нижний и верхний радиусы боковой поверхности образца. В начальном приближении коэффициент трения задается равным 0,15. Число итераций обычно не превышает трех при погрешности в определении высоты арки менее 1 %. Далее при фиксированных коэффициентах трения производится уточнение динамических диаграмм деформирования по аналогичной рассмотренной выше методике. На рис. 2 схематично представлена процедура методики построения истинных диаграмм деформирования и определения коэффициентов трения в экспериментах на сжатие.

Проведен ряд экспериментально - расчетных исследо ваний компактных цилиндрических образцов из стали 10 Г 2 ФБЮ при растяжении и сжатии . В экспериментах на растяжение использовались цилиндрические стержни с начальной длиной рабочей части L 0 = 10 мм и начальным диаметром d 0 = 5 мм, для экспериментов на сжатие – образцы-таблетки с начальной длиной рабочей части L 0 = 15 мм и начальным диаметром d 0 = 10 мм. Численное решение задачи проводилось в динамической осесимметричной постановке. На рис. 3 представлен вид исследуемых образцов и соответствующие им дискретные расчетные модели. Для квазистатических экспериментов скорость принималась U i = 0,1 м/с, а для динамических экспериментов - U i = 10 м/с.

Исходные данные

Итерационная процедура

Численный расчет

Критерий останова |(f_s-f_p)/f₃|s6

Корректировка диаграммы деформирования ^лгд- ®, = Рч,

Выходные данные

•Геометрия исследуемого образца

•Зависимость осевой силы F₃ от удлинения образца, полученная в эксперименте

Начальное приближение диаграммы деформирования

Истинная диаграмма деформирования j,=’₍«

Рис. 1. Процедура методики построения истинных диаграмм деформирования в экспериментах на растяжение

Fig. 1. Diagram of the method for constructing true deformation diagrams in tensile experiments

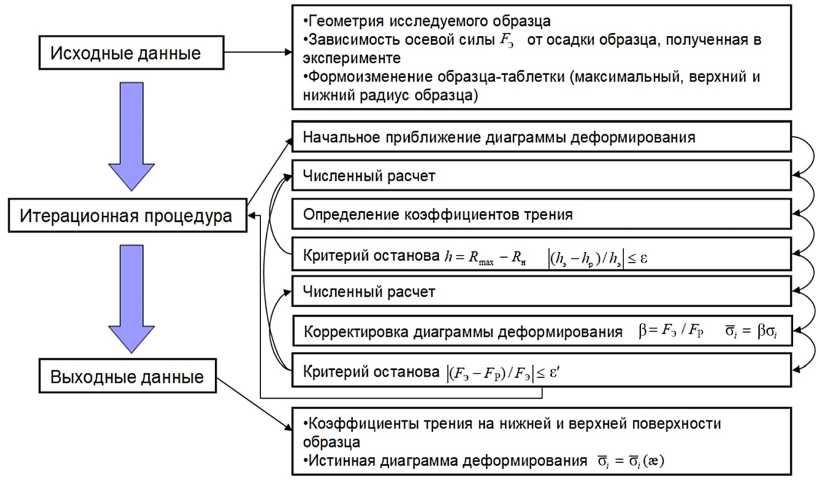
Рис. 2. Процедура методики построения истинных диаграмм деформирования в экспериментах на сжатие

Fig. 2. Diagram of the method for constructing true deformation diagrams in compression experiments

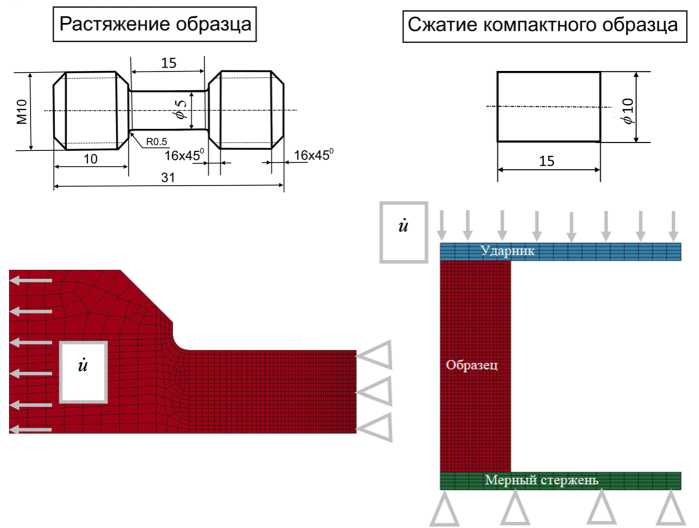
Рис. 3. Внешний вид образцов и соответствующие им дискретные расчетные модели

Fig. 3. Samples and corresponding discrete calculation models

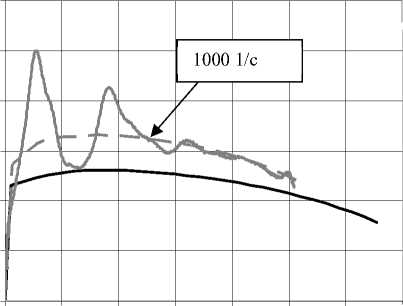
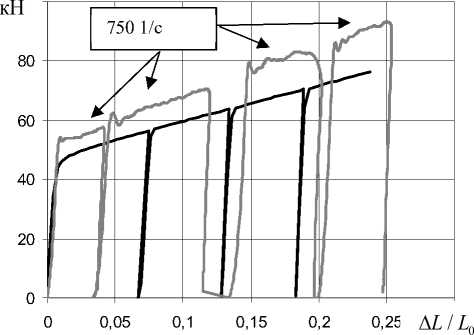
Испытания на сжатие компактных образцов проводились в четыре этапа с использованием ограничителей перемещений. Поэтапное нагружение позволяет с большей точностью получить зависимость осевых сил от скорости деформаций. На рис. 4 представлены экспериментальные зависимости осевой силы от удлинения (осадки) стали 10Г2ФБЮ. Пунктирная серая линия на рис. 4 является аппроксимацией экспериментальной зависимости осевой силы от удлинения при динамическом растяжении сплошного стержня. На основе разработанных экспериментально-расчетных методик с погрешностью по осевым силам менее 0,5 % построены квазиста-тические и динамические истинные диаграммы деформирования стали 10Г2ФБЮ, которые приведены на рис. 5. На рис. 6 показаны распределение параметра Од-квиста æ и формоизменение исследуемых образцов с учетом полученных диаграмм деформирования при удлинении AL / L0 = 0,2 .

Построенные квазистатические истинные диаграммы деформирования стали 10Г2ФБЮ (см. рис. 5), полученные при растяжении и сжатии компактных образцов, достаточно хорошо согласуются. Установлено, что при скоростях деформаций до 500 1/c динамические диаграммы деформирования незначительно отличаются от квазистатических, а при скоростях деформаций выше 500 1/c влияние скорости деформаций существенно возрастает на поведение материала при динамическом деформировании. Следует отметить, что динамическая диаграмма деформирования при растяжении (см. рис. 5, серая сплошная линия) получена без учета влияния величин скоростей деформаций, реализующихся в зоне локализации пластического деформирования (образование «шейки»), так как после образования «шейки» в этой зоне скорости деформаций значительно выше 1000 1/c. Квазистатические и динамические эксперименты на растяжение компактных образцов проводились до разрушения. При динамическом и квазистатическом растяжении полученные величины относительных сужений образцов после разрушения в минимальном сечении «шейки» в пределах экспериментальной погрешности совпадают.

F, кЬ

0    0,05    0,1    0,15    0,2    0,25    0,3 Л1

Растяжение стержней

Сжатие образцов

Рис. 4. Экспериментальные зависимости осевой силы от удлинения (осадки) образцов при квазистатическом (черные линии) и динамическом (серые линии) нагружении

Fig. 4. Experimental dependences of axial force on elongation of samples under quasi-static (black lines) and dynamic (gray lines) loading о,., МПа

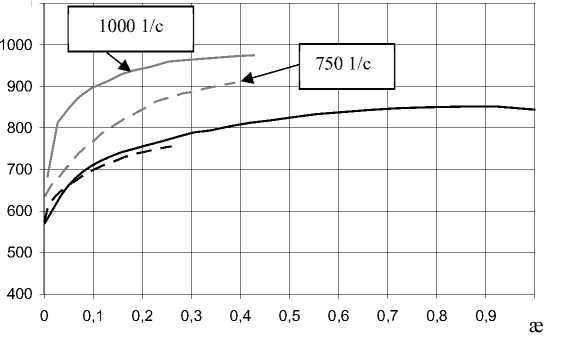
Рис. 5. Построенные истинные диаграммы деформирования стали 10Г2ФБЮ в экспериментах на растяжение (сплошные линии) и сжатие (пунктирные линии) цилиндрических образцов при квазистатическом (черные линии) и динамическом (серые линии) нагружении

Fig. 5. Constructed true deformation diagrams of 10G2FBU steel in tensile (solid lines) and compression (dashed lines) experiments on cylindrical samples under quasi-static (black lines) and dynamic (gray lines) loading

4.266e-01

3.839e-01

3.413e-01

2.986e-01 2.5596-01 2.133e-01 1.70Se-01 1^806-01 8.5326-02 4.2886-02 0.000e+00

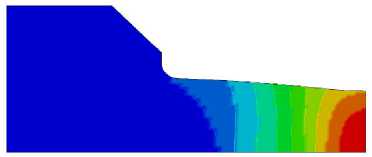
Квазистатическое нагружение

4.752e-01

4.277e-01

3.8016-01

3.326e-01

2.376e-01

1.901e-01

1.426e-01

9.504e-02

4.752e-02

0.000e+00

Динамическое нагружение

2.413e-01

2.1716-01

1.9296-01

1.687e-01 _

1.445e-01 _

1.203e-01 _

9.6126-02

7.1936-02

4.7746-02

2.354e-02

-6.519e-04

3.184e-01

2.865e-01

2.5470-01

2.2280-01

1.9090-01

1.5900-01

1.2710-01

9 5250-02

6 3360-02

3.148B-02

-3.9710-04

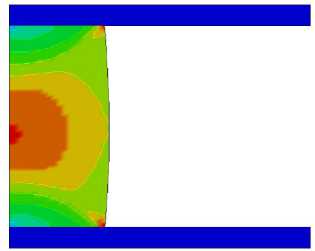
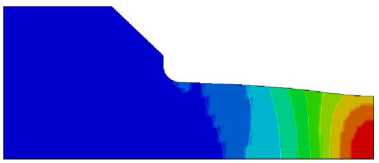
Рис. 6. Распределение параметра Одквиста æ и формоизменение исследуемых образцов с учетом полученных диаграмм деформирования при удлинении A L / L 0 = 0,2

Fig. 6. Distribution of the Odquist parameter æ and the change in shape of the studied samples taking into account the obtained deformation diagrams during elongation A L / L ₀ = 0,2

Болт с резьбовой рабочей частью

Рис. 7. Внешний вид болтов М8 и соответствующие им дискретные расчетные модели

Fig. 7. M8 bolts and corresponding discrete calculation models

Разработанные экспериментально-расчетные методики позволяют строить диаграммы деформирования при деформировании элементов конструкций до момента разрушения. Рассмотрим квазистатическое растяжение болтов М8 с гладкой и резьбовой рабочей частью из стали Ст35. Болты с гладкой рабочей частью имели начальный радиус R = 2 мм и начальную длину L0 = 15,9 мм, а с резьбовой рабочей частью – начальный внешний радиус резьбы R 0 = 4 мм и начальное расстояние между головкой и гайкой L0 = 16 мм. На рис. 7 представлен вид исследуемых болтов М8 и соответствующие им дискретные расчетные модели. При моделировании деформирования образцов с гладкой рабочей частью наличием резьбы пренебрегали. В образцах с резьбовой рабочей частью решалась контактная задача взаимодействия болта с массивной гайкой, внешняя часть которой полагалась жестко закрепленной. Скорости осевых перемещений головок болтов задавались ui =0,1 м/c. Для болта с резьбовой рабочей частью проводился сравнительный расчетный анализ результатов моделирования в трехмерной и осесимметричной постановках. Полученное отличие в осевых силах при одинаковых перемещениях составило менее 1 %. Поэтому построение истинных диаграмм деформирования при растяжении болтов проводилось в осесимметричной постановке.

Полученные экспериментальные зависимости осевых сил ( F ) от удлинения ( u ) для рассмотренных болтов представлены на рис. 8. Построение истинных диаграмм деформирования для стали Ст35 проводилось с погрешностью по осевым силам менее 0,1 %.

На рис. 9 представлены построенные истинные диаграммы деформирования стали Ст35 для болтов М8 с гладкой и резьбовой рабочей частью. На рис. 10 показаны распределение параметра Одквиста æ и формоизменение болтов М8 с учетом полученных диаграмм деформирования при удлинении A L / L 0 = 0,0875 .

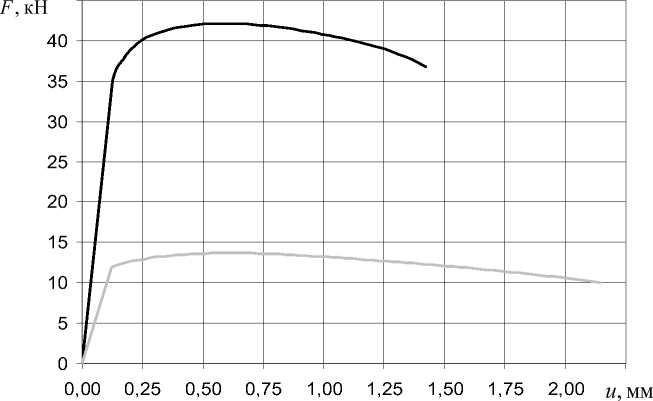
Рис. 8. Экспериментальные зависимости осевой силы от удлинения для болтов М8 с гладкой (серая линия) и резьбовой (черная линия) рабочей частью из стали Ст35

Fig. 8. Experimental dependences of axial force on elongation for M8 bolts with smooth (gray line) and threaded (black line) working parts made of St35 steel

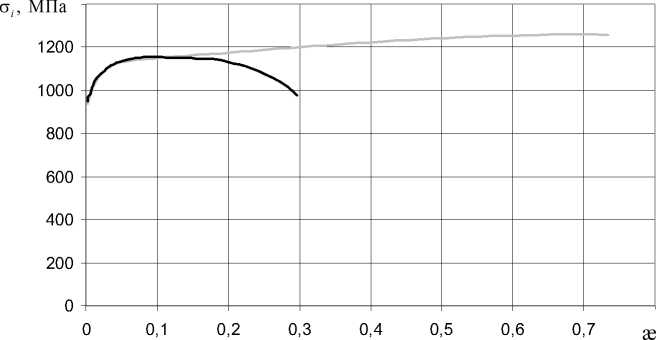
Рис. 9. Построенные истинные диаграммы деформирования для болтов М8 с гладкой (серая линия) и резьбовой (черная линия) рабочей частью из стали Ст35

Fig. 9. Constructed true deformation diagrams for M8 bolts with smooth (gray line) and threaded (black line) working parts made of St35 steel

3.046e-01

2.742е-01

2.437е-01

2.133е-01

1.828е-01

1.523е-01

1.219е-01

9.139е-02

6.093е-02

3.046е-02

0.000е+00

Болт М8 с гладкой рабочей частью

3.626е-01

3.262е-01

2.898е-01

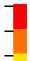
2.534е-01

2.170е-01 1.806е-01 1.442е-01 1.078е-01 7.1436-02 3.5046-02

-1.3576-03

Болт М8 с резьбовой рабочей частью

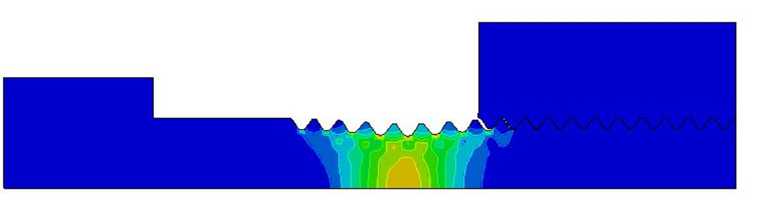
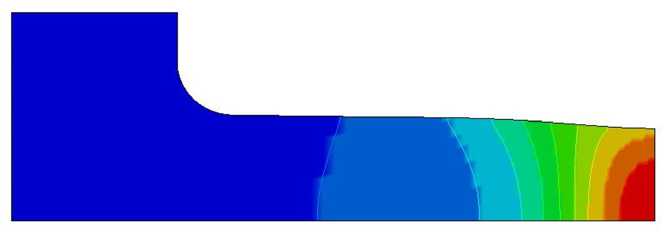
Рис. 10. Распределение параметра Одквиста æ и формоизменение болтов М8 с учетом полученных диаграмм деформирования при удлинении Л L / L 0 = 0,0875

Fig. 10. Distribution of the Odquist parameter æ and the change in shape of M8 bolts taking into account the obtained deformation diagrams during elongation Л L / L ₀ = 0,0875

Из полученных результатов видно, что истинные диаграммы деформирования болтов из стали Ст35 мало различаются. Однако для болта с резьбовой рабочей частью истинная диаграмма деформирования имеет ниспадающий участок, и разрушение происходит при значительно меньших значениях параметра Одквиста. Отличия диаграмм деформирования обусловлены существенным влиянием у болта с резьбовой рабочей частью наличия концентраторов напряжений.

Определение материальных параметров модели разрушения упругопластических материалов

Для исследования и описания процессов разрушения упругопластических материалов будем использовать связанную модель разрушения на основе кинетического уравнения накопления повреждений в сочетании с критерием прочности типа Писаренко – Лебедева. Критерий прочности записывается следующим образом [26]:

XO ⁺ (1 ^- X> i• ' " = о p , (1)

где σ _i – интенсивность напряжений, Ж _о = (о ₁ + о ₂ + о ₃ ) / о_t, о 1 , о ₂ , о ₃ - главные напряжения, A <  1 - параметр неоднородности материала, х - параметр, характеризующий степень хрупкости материала,

σ _P – предел прочности на растяжение. Первое слагаемое в (1) характеризует упругопластические, а второе – хрупкие свойства материала при разрушении. Широкий диапазон изменения коэффициента 0 < X <  1 позволяет учитывать особенности свойств материала и его склонность к разрушениям отрывом или сдвигом. Предельные значения % = 1 и X = 0 описывают поведение идеально пластичных и идеально хрупких материалов соответственно.

Далее проведем преобразования критерия прочности и запишем выражение для максимального главного напряжения σ ₁ через инвариантные характеристики вида текущего напряженного состояния ф _а , ^ _а следующим образом:

° 1 = 3 O , [ ^2cos^ a ) ⁺ Ж о ] • ⁽²⁾

Отметим, что величина cos( ф _a ) в (3) меняется в пределах от 1 до 0,5. С учетом соотношения (2) критерий прочности (1) представим в следующем виде:

0 , 3 [ з % + (1 - X )(2 cos^ a ) + V ) A '" ] = ° P • (3)

Таким образом, предельное значение интенсивности напряжений, исходя из полученного соотношения (3):

*

σ i =

σ p

χ + ^{(1 -} ₃ ^{χ )} ( 2cos( φ σ ) + ψ σ ) A ^{1-ψ σ}

В качестве кинетического уравнения накопления повреждений рассматривается схема линейного суммирования повреждений с учетом функции влияния [27–31]:

λ

ω=              ,

λ ^* f ( ψ _σ , φ _σ ,...)

где λ – переменная, параметризующая процесс упругопластического деформирования, λ ^* – предельное значение этой переменной, f ( ψ _σ , φ _σ ,...) – безразмерная функция, характеризующая влияние вида НДС на степень по-врежденности материала, ψ _σ – коэффициент жесткости напряженного состояния, φ _σ – угол фазы девиатора напряжений.

Для пластичных материалов в модели разрушения в качестве параметра λ будем использовать параметр Од-квиста æ. В связи с этим соотношение (5) примет вид:

(b =

сё

æ _pf ( ψ_σ , ϕ_σ ) ^,

где æ _p – предельное значение параметра Одквиста при растяжении. В качестве функции влияния с учетом критерия прочности Писаренко – Лебедева (4) будем рассматривать:

f ( ψ _σ , φ _σ ) =

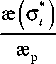
где æ ( σ ^* _i ) – обратная функция истиной диаграммы деформирования, т.е. зависимость параметра Одквиста от интенсивности напряжений.

Связанная модель разрушения [32] обычно реализуется с учетом влияния параметра поврежденности ω на свойства материала. Зависимость предела текучести, упругих характеристик материала обычно задается в виде степенной зависимости от параметра поврежденности:

K = K ( 1 -ω ⁿ ) ;

G = G ( 1 -ω ⁿ ) ;

σ _i =σ _i (æ) ( 1 -ω ⁿ ) ;

где K , G – упругие характеристики материала модуль объемного сжатия и модуль сдвига соответственно, σ _i (æ) – истинная диаграмма деформирования. Параметр n определяет скорость изменения свойств материала при росте параметра поврежденности.

В связанной модели связь между скоростью девиатора напряжений о j и скоростью упругих составляющих девиатора деформаций е j определяется в виде:

• оj = 2 Ge’ + G oj,, G = — (b, ij        ij G ij где оj - скорость девиатора напряжений, ej - скорость упругих составляющих девиатора деформаций, G – модуль сдвига;

KdK

σ=3Ke+ σ, K =ω, Kd где о и е - скорость шаровых составляющих напряжений и деформаций, K – модуль объемного сжатия. Предложенная связанная модель разрушения реализована в виде модели упругопластического материала с изотропным упрочнением. Необходимо отметить, что для соотношения (5) вводилось ограничение параметра повреждения ω=0,98 , выражающее исчерпание возможностей материала упругопластически деформироваться. При достижении этой величины параметр повреждения не изменялся.

На основе экспериментально-расчетного подхода разработана методика идентификации материальных параметров связанной модели разрушения. Для оснащения модели разрушения целесообразно использовать эксперименты на растяжение сплошных стержней. В качестве примера рассмотрим растяжение болтов М8 с гладкой и резьбовой рабочей частью из стали Ст35. С учетом построенных истинных диаграмм деформирования Ст35 (рис. 9) из имеющихся экспериментальных результатов (зависимость осевой силы от удлинения, вид разрушения болтов) необходимо определить значения параметров A , χ , σ _P и n . Сложностью определения материальных параметров является их взаимосвязь. Следует отметить, что полученный ниспадающий участок истинной диаграммы деформирования (см. рис. 9) для болта М8 с резьбовой рабочей частью в дальнейшем описывается связанной моделью накопления повреждений. Методика определения материальных параметров состоит из трех следующих этапов.

• 1.    Изначально фиксируются параметры A = 0,9 и χ = 0,9 как средние значения для упругопластических материалов. Выполняется два расчета с параметрами n = 10 и n = 20, а предел прочности принимается соответственно σ _P = 1,1 ⋅ σ ^* _P и σ _P = 1,2 ⋅σ ^* _P , где σ ^* _P – максимальное значение интенсивности напряжений на построенной истинной диаграмме деформирования (см. рис. 9). Далее осуществляется итерационный процесс определения параметров σ _P и n посредством линейной интерполяции (экстраполяции) до совпадения расчетной и экспериментальной зависимостей осевых сил вплоть до

• 2.    Материальные параметры A и χ в большей степени характеризуют вид разрушения образцов отрывом и (или) сдвигом. По поверхности разрушения образца при растяжении количественно определяется радиус, характеризующий область разрушения образца в виде отрыва. На основе этого осуществляется итерационный процесс определения параметров A и χ посредством линейной интерполяции (экстраполяции) до полного совпадения вида и характера разрушения образца.

• 3.    По определенным параметрам A и χ при различии начала процесса разрушения при растяжении (последняя точка на экспериментальной кривой осевой силы) уточняются параметры σ _P и n .

начала процесса разрушения при растяжении (последняя точка на экспериментальной кривой осевой силы рис. 8).

На основе предложенной методики для болтов М8 с гладкой и резьбовой рабочей частью из стали Ст35

определены материальные параметры модели разрушения, которые представлены в таблице.

Материальные параметры связанной модели разрушения

Material parameters of the coupled fracture model

Болт М8	A	χ	σ P , МПа	n
С гладкой рабочей частью	0,96	0,97	1275,2	20
С резьбовой рабочей частью	0,97	0,99	1198	20

На рис. 11 приведены зависимости экспериментальной (сплошная серая линия) и расчетной (пунктирная линия) осевой силы от перемещения при растяжении болтов М8 с гладкой (кривая 1 ) и резьбовой (кривая 2 ) рабочей частью. На рис. 12 и 13 представлены численные результаты развития повреждений ω и внешний вид разрушения, полученный в эксперименте, для болтов М8 с гладкой и резьбовой рабочей частью соответственно.

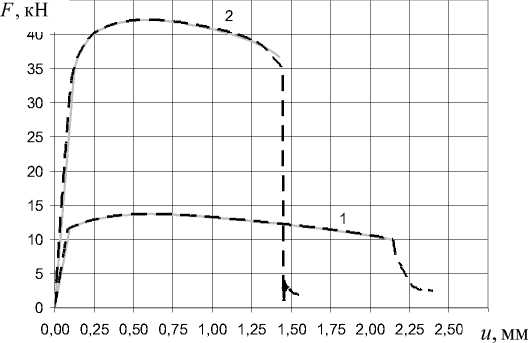
Рис.11. Зависимости экспериментальной (сплошные серые линии) и расчетной (пунктирные линии) осевой силы от перемещения при растяжении болтов М8 с гладкой (кривая 1 ) и резьбовой (кривая 2 ) рабочей частью

Fig. 11. Dependences of the experimental (solid gray lines) and calculated (dashed lines) axial force on the displacement during tension of M8 bolts with a smooth (curves 1 ) and threaded (curves 2 ) working part

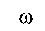
9.800e-01

8.820^-01

7.840e-01

6.860 e-01

5.880e-01

4.900e-01

3.920e-01

2.940e-01

1.960e-01

9.800e-02

0.000e+00

Рис. 12. Численные результаты распределения повреждений ω и внешний вид разрушения, полученный в эксперименте, для болта М8 с гладкой рабочей частью

Fig. 12. Numerical results of damage distribution and destruction obtained in the experiment for an M8 bolt with a smooth working part

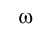
9.800e-01

8.820e-01

6.860e-01

5.8S0e-01

4.900e-01

3.920e-01

2.940e-01

1.960e-01

9.800e-02

0.000e+00

Рис. 13. Численные результаты распределения повреждений ω и внешний вид разрушения, полученный в эксперименте, для болтов М8 с резьбовой рабочей частью

Fig. 13. Numerical results of damage distribution and destruction obtained in the experiment for M8 bolts with a threaded working part

Как видно из представленных численных результатов на рис. 11–13, при использовании двухпараметрической модели Писаренко – Лебедева процесс зарождения и распространения повреждений качественно и количественно описывает экспериментальные данные. При растяжении болта М8 с гладкой рабочей частью первоначально разрушение реализуется вблизи его оси отрывом, а в дальнейшем распространяется к свободной поверхности и трансформируется в сдвиговое разрушение (рис. 12). В итоге полученная поверхность разрушения напоминает форму «чашечки», что является широко известным экспериментальным фактом.

Заключение

Таким образом, представлена новая экспериментально-расчетная методика идентификации материальных параметров предложенной связанной модели разрушения на основе кинетического уравнения накопления повреждений в сочетании с критерием прочности типа Писаренко – Лебедева. Определены материальные параметры предложенной связанной модели разрушения для стали Ст35. Представлены результаты численного моделирования процесса разрушения болтов М8 с гладкой и резьбовой рабочей частью при растяжении. В итоге