Применение элементов теории погрешностей при оценке рисков управленческих решений в экономике

Рассмотрим деятельность некоторой коммерческой организации, конечной целью которой является получение прибыли. В большинстве случаев эта деятельность сопровождается принятием последовательности управленческих решений, разнесенных, как правило, во времени [1]. В рыночных условиях лицо, принимающее решение (ЛПР), может находиться в условиях либо полной неопределенности, когда не известны вероятности исходов событий, являющихся следствием принятого решения, либо в условиях частичной неопределенности, если заданы вероятности наступления того или иного исхода. Причем среди возможных исходов имеются и такие, которые препятствуют достижению конечной цели - получению прибыли.

Фактически ЛПР управляет сложной неопределенной системой, и эффективность такого управления в основном определяется качеством прогнозирования динамики ведущих факторов, влияющих на процесс достижения конечной цели, грамотным учетом этих факторов и умением изменять эти факторы в свою пользу [2]. При принятии решения ЛПР может ориентироваться на величину ожидаемой или наиболее вероятной прибыли, которую обозначим П .

Любое управленческое решение связано с определенным риском по отношению к конечной цели, и этот риск находится в тесной корреляции с величиной возможных отклонений от наиболее вероятного значения ожидаемой прибыли 5П[3]. Эта величина 5П вместе с прибылью П в большей степени определяет результат любого коммерческого или финансового проекта и является основным фактором, влияющим на необходимость принятия того или иного решения, исход которого может быть благоприятным или неблагоприятным для ЛПР. К числу благоприятных отнесем два ис хода: получение ожидаемой прибыли П и получение прибыли, превышающей П. Неблагоприятных исходов может оказаться больше. Перечислим основные из них [4]:

• -    недополучение ожидаемой прибыли;

• -    получение дохода меньшего, чем затраченные средства (отсутствие прибыли);

• -    отсутствие каких-либо доходов;

• -    прямые убытки от операции, приводящие к ущербу вплоть до потери собственности.

Считается, что проект с меньшей величиной является менее рискованным [5]. Удобство применения величины в оценке риска проекта объясняется тем, что эта величина выражается во вполне определенных абсолютных единицах, например, в рублях, а также может быть представлена в относительной форме как коэффициент вариации, показывающий степень риска на единицу средней прибыли. Эту стохастическую величину будем называть также вариацией прибыли.

Для оценки величины на основе традиционных методов ан ализа статистических данных и теории погрешностей экспериментальных данных предлагается следующий алгоритм.

• 1.    С помощью корреляционного анализа определяется вектор ведущих факторов X = Х_; , X 2 , ... X m , наиболее тесно связанных с величиной П , где m - число ведущих факторов.

• 2.    Выявляется функциональная зависимость результативного признака П от ведущих факторов X , и представляется эта зависимость в аналитическом виде:

• 3.    Оцениваются наиболее вероятные значения ведущих факторов и величины их случайных отклонений (вариаций) XX = ( 5X_; , 5X 2 ,..., X m ) от X . Эти оценки могут быть получены либо с исполь-

• зованием метода экспертных оценок, либо в результате статистического анализа имеющихся прошлых данных Х, либо, что наиболее важно в практической деятельности, интуитивно, при достаточном опыте работы ЛПР.

• 4.    Определяется величина вариации при были (абсолютная погрешность) по правилу квадратичного суммиров ания погрешностей [6]:

  3 П

  

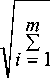
  д ПК

  8 X • V ¹

  
  

• 5 .    Анализируется чувствительность величин Π и δ Π , принимается окончательное решение

. . П = f (X X ... ^X m ) , , . ⁽¹⁾

л ² и ^3X i , X J

д/ где/axi- операция вычисления частых производных функции m переменных П при наиболее вероятных значениях Х [7].

на основе этого анализа. Достоверность полученной оценки δ Π определяется в основном качеством построенной функциональной зависимости (1), т.е. тем, н асколько правильно ЛПР моделирует экономический процесс.

Иллюстрацию применения предложенного алгоритма проведем на примере [8]. Руководство рассматривает инвестиционный проект, связанный с выпуском нового изделия. Требуется провести анализ проекта и определить условия реализации проекта, обеспечивающие достижение основной цели – получение прибыли.

Предположим, что предварительные процедуры, включающие выбор ведущих факторов Х, оц ен ку их наиболее вероятных значений Х и возможных отклонений ЗХ,,3Х2,...,3Xm, проведены, результаты сведены в таблице 1.

Таблица 1

Ведущие факторы	Наиболее вероятные значения	Вариации факторов
Объем выпуска, Q	200	30
Цена единицы изделия, Р	50	5
Переменные затраты, V	30	5
Постоянные затраты, F	500	20
Амортизация, А	100	20
Налог на прибыль, Т	40%	5%
Норма дисконта, r	15%	5%
Срок проекта, n	5	1
Остаточная стоимость, S	200	50
Начальные инвестиции, I	2000	50

Исходны е данные для проведения анализа

Представленная таблица содержит результаты выполнения пунктов 1, 3 предложенного алгоритма. В настоящей статье нет необходимости описывать механизм выбора ведущих факторов и их оценки, так как этой теме посвящено большое количество учебной литературы.

Для выбранных ведущих факторов функциональная зависимость для функции прибыли П может быть представлена в виде:

_П = n Q ( P - V )(1 - T ) - F (1 - T ) + T • A +

⁵=1                  (1 + r )⁵                      (3)

S

+ (TT75n- I0, где будущие поступления от проекта приведены к современной стоимости (дисконтированы) на момент инвестирования денежных средств.

Выражения для частных производных, используемых в оценке вариации функции при- были (2), получаются путем последовательного дифференцирования функции (3) по всем переменным, в результате получается 10 соотношений:

а п = t ( p - v )(i - т ) d Q ” * = 1 (1 + r ) *    ’

дП = .nQ (1 - T) dP "*^1 (1 + r) * , (5) an = _ q (1 - т) d V " t! (1 + r) * , (6) an  _n^ (1 -t ) af = ^^11 + r) *, (7) an = <1 т aa "£141+r) *, (8) аП n^F + A - Q (P - V)

a T "tt     (1 + r ) *

дП_ n^Q(PP-V)(1-T) -F(1-T)+T• A ar" S          (1+r)'+1           1

S • n

- (1 + r ) ^{n +1}

a n _ Q ( P - V )(1 - T ) - F (1 - T ) + T • A

5 » "                (1 + r ) ^{n + 1}                ,

a n _    1

a S ” (1 + r ) ⁿ , д П _- 1 .

д S

Подставив соотношения (4)-(13) и оценки отклонений факторов 5 Х в соотношение (2), получим выражение для величины воз м ожного отклонения δΠ от ожидаемой прибыли Π в виде:

n ( P - V )(1 - T ) _5Q 1² fА _Lv t _ 1      (1 + r ) t         ⁶7   I S

2 nnn

+ у ^{(1 T} ) • 5 f | +|y— T_ • 5 a | +|y

V^s (1 + r ) t 7 V^s (1 + r ) t 7 V^s

+ Г ^ e ⁽ P - V ⁾⁽1 - T ) - F ⁽i - T ) + T ■ A

vv "

5 П _ I Z

Q (1 - t ) (1 + r ) t

2 _n

• ^{5 P} I + Z

V t _ 1

^Q • 5 V | 2 +

(1 + r ) t 7

^{F +} A ^{- Q ( P -} V ) • 5 T ) +

г

(1 + r ) '

S • n '

+

(1 + r )' ^{+ 1}

t +

(1 + r ) ^{n + 1}

^ • 5 r

+

Q ( P - V )(1 - T ) - F (1 - T ) + T • A

(1 + r ) ^{n + 1}

• 5 n

Г 1

+ I ---------

V (1 + r )

F • 5 S + ( 5 1 ) 2

.

Рассмотрим некоторые задачи , которые могут быть поставлены и решены на основе соотношений (3) и (14).

Во-первых, это задача оптимизации, которая заключается в максимизации целевой функции прибыли П и минимизации вариации прибыли б П при изменении факторов Хв пределах заданных отклонений §Х от своих наиболее вероятных значений Х. Хотя эта задача даже в самом простом случае является задачей нелинейного математического программирования, она может быть решена с помощью стандартных прикладных пакетов, например, с помощью приложения MS Excel.

Во-вторых, проведение анализа чувствительности прибыли П и вариации 5 П под воздействием факторов Х . В качестве иллюстрации на рисунке 1 прив едены зависимости прибыли Π и ее вариации δ Π от величины налога на прибыль Τ.

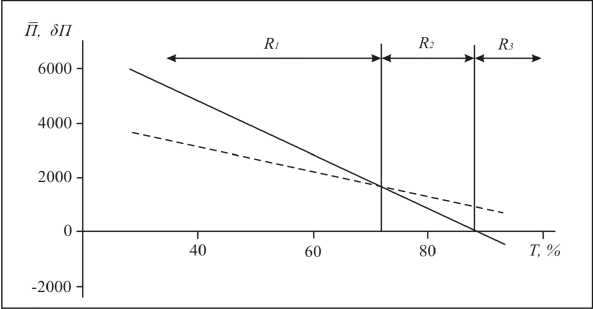
Рис. 1. Зависимости П(Т) (сплошная линия) и 5 П(Т) (пунктирная линия)

Можно выделить три характерные области: область R₁ соответствует минимальному риску, в ней П >  5 П , т.е. здесь прибыль всегда положительна; область R₂ характеризует возможные исходы, при которых поступления от проекта могут быть меньшими, чем первоначальные затраты; и, наконец, область R₃ соответствует прямым убыткам.

С целью оценки ошибки, возникающей^ задаче из-за неточного определения Х и 5 Х , проведены расчеты относительных погрешностей прибыли ( ^ ПП ) и вариации прибыли

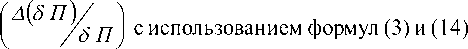
при искусственном внесении абсолютного отклонения в размере 50% в величины Х и З Х .

Результаты расчетов представлены в таблице 2.

Можно сформулировать три_очевидных вывода.

Во-первых, изменение Х на 50% оказывает серьезное влияние на ключевые показатели прибыли П иее вариации ЗП .

Во-вторых, существенное изменение вариаций З Х практически не оказывает влияния на величину ЗП , т.е. оценку вектора З Х можно проводить,

Результаты анализа чувствительности, в

( _ а п/ п х V 7	А^п¥ ( ? ) /ЗП Х V 7	" ( З П Зз П ( З Х 1 V 7
76,3	45,7	7,6
190,7	52,3	20,0
-114,4	15,3	20,0
-9,5	1,1	0,01
1,3	0,1	0,004
-43,2	31,9	1,8
-21,6	17,1	4,0
17,3	12,2	4,6
0,5	0,0	0,001
-19,0	0,0	0,014

Визуализация рассматриваемой задачи может быть осуществлена путем построения полей прибыли и вариации прибыли.

Функции П и ЗП, определяемые формулами (3) и (14), зависимы от m = 10 различных факторов Х. Эти функции могут быть изображены в виде поверхностей в (m + 1)-мерном пространстве действительных чисел [9]. Исследуя такие поверхности с помощью градиента скалярной функции, можно определить области максимального значения прибыли Пили области минимального значе как и было отмечено выше, интуитивно, не используя специальные математические методы.

Третий вывод заключается в том, что среди десяти ведущих факторов Х два оказывают наибольшее влияние на величину прибыли П и ее вариацию ЗП . Это цена единицы изделия Р и величина переменных затрат V . Хотя этот вывод относится только к рассматриваемому примеру, его используем для построения полей и вариации прибыли.

Таблица 2 % ния ЗП, отвечающего за риск при принятии решения. Эти области соответствуют факторам Х, наиболее приемлемым для ЛПР в случае выбора того или иного варианта управленческого решения.

Ввиду того что в нашем примере на функцию П и ее вариацию ЗП оказывают существенное влияние два фактора Р и V (по сравнению с остальными используемыми), то поверхности П = ф (Р,У ) и З П - у (P,V) изображаются в трехмерном пространстве (см. рис. 3, 4).

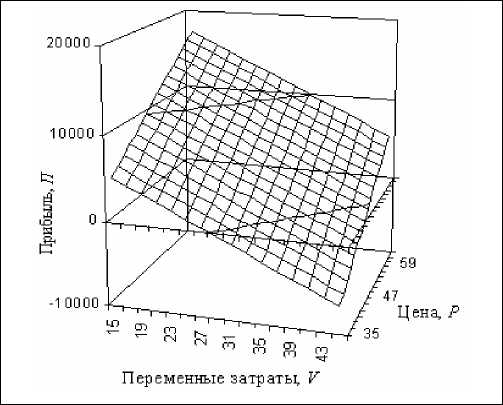
Рис. 3. Поверхность прибыли П -ф (РУ)

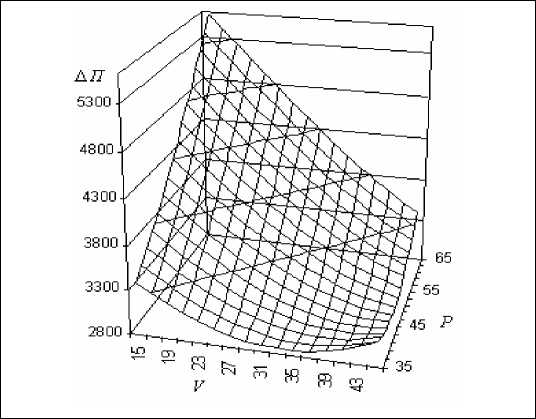
Рис. 4. Поверхность вариации прибыли δ П = ψ (P,V)

Данные поверхности можно интерпретировать как поля в двумерном пространстве ( P , V ). Зависимость П = ϕ ( P ,V ) – линейная и монотонно возрастающая, поэтому рисунок 3 является скорее иллюстративным, чем информативным, т.е. он подтверждает очевидный факт – прибыль производящего предприятия увеличивается с ростом цены на изделия Р и снижением затрат на их производство. На рисунке 4 имеется минимум функции вариации δ П , который состоит из множества точек, соотв етствующих решению уравнения V = 0,85 ⋅ P - 1,3 . Это уравнение позволяет определить рекомендуемую величину переменных затрат при производстве изделий, при которых риск проекта будет минимальным. В случае более сложных зависимостей (3) и (14) по-верхн ости П и δ П могут иметь несколько экстремумов, которые указывают ЛПР варианты решений, влекущих за собой минимальный риск или направленных на достижение максимальной прибыли.

Итак, нами предлож е н алгоритм оценки величины будущей прибыли П с указанием ее возможного отклонения δ П , основанный на заранее разработанной функциональной зависимости функции прибыли П от ведущих факторов. Для применения данного алгоритма требует → с я знание наиболее веро-ятных→^значений факторов Х и их возможных вариаций δ Х . Показано, что д→аже значительные ошибки в определении вектора δ Х не сильно влияют на величину оценки δ П , что позволяет ЛПР интуитивно, и→мея только практический опыт работы, определять δ Х . Предложенный алгоритм апробирован на модельном проекте, в ходе которого показана возможность постановки и решения оптимизационной задачи, проведения анализа чувствительности и построения полей прибыли и ее вариации. Для практического применения предложенной схемы не существует принципиальных ограничений. Трудоемкие расчеты на основе алгоритма могут быть проведены с помощью доступной программы, созданной для персонального компьютера.

• 1.    Эддоус М., Стэнсфилд Р. Методы принятия решения. М., 1997. С. 290.

• 2.    Ременников В.В. Разработка управленческого решения. М., 2000. С. 135.

• 3.    Малыхин В.И. Финансовая математика. М., 1999. С. 125.

• 4.    Там же.

• 5.    Там же.

• 6.    Рабинович С.Г. Погрешности измерений. Л., 1978. С. 180.

• 7.    Сюдсетер К., Стрём А., Берк П. Справочник по математике для экономистов. СПб., 2000. С. 129.

• 8.    Лукасевич И.Я. Анализ финансовых операций. М., 1998. С. 230.

• 9.    Воеводин В.В. Линейная алгебра. М., 1980. С. 230.