Применение энергостатического метода определения усилий и моментов, действующих на инструмент при прошивке на двухвалковых станах поперечно-винтовой прокатки с приводными направляющими дисками

В настоящее время наблюдается тенденция увеличения производительности процесса прошивки на двухвалковых станах поперечно-винтовой прокатки [1]. Интенсификация любого процесса обработки металлов давлением сопровождается ростом энергосиловых параметров (ЭСП) процесса [2]. При этом увеличиваются нагрузки на механизмы прокатного оборудования, что влияет на точность получаемого изделия и на срок эксплуатации оборудования. Поэтому определение усилий и моментов, действующих на рабочий инстру-

мент прошивного стана, является важной и актуальной задачей.

Процесс прошивки является достаточно сложным с точки зрения математического описания из-за большого количества разнородных факторов, задающих различные по своей природе, но тесно взаимодействующие друг с другом явления [3]: позиционирование прокатного инструмента прошивного стана; модель поведения материала с учетом изменяющегося температурного поля заготовки; вращающийся инструмент, приводящий к необходимости

введения алгоритмов определения контактного взаимодействия узлов на поверхностях заготовки и инструментов; сложная геометрия очага деформации, обусловленная искажением из-за углов подачи и раскатки.

С развитием численных методов математического анализа, особенно метода конечных элементов, стало возможным решать объемные задачи в общих (с точки зрения входящих в модель систем уравнений) постановках [4].

Но большое количество элементов расчетной сетки, необходимое для уменьшения погрешности описания твердотельной модели и, соответственно, получаемых результатов численного моделирования, в сравнении с реальными данными, приводит к излишней громоздкости конечно-элементных моделей процессов прошивки и сильно увеличивает время, затрачиваемое на их расчет.

С другой стороны, с использованием возможного ряда допущений представляется возможным получить аналитические зависимости в явном виде для определения полного нормального усилия, действующего на инструмент, а также сил трения и вращающих моментов. В сравнении с численными методами расчета данный подход позволяет заметно проще и намного быстрее вычислять интегральные характеристики процесса, при этом незначительно уступая в точности.

Одним из подходов к исследованию процессов прокатки является энергетическая теория взаимодействия инструмента и деформируемого металла, впервые сформулированная и развитая Выдриным Владимиром Николаевичем в своих трудах [5]. В основе этой теории лежит использование закона сохранения энергии, которому подчиняется взаимодействие металла и инструмента при прокатке. Особенность применения энергетической теории взаимодействия инструмента и деформируемого металла при поперечно-винтовой прокатке заключается в разнообразии условий работы инструмента, в сложном характере деформации и скольжении металла на контактных поверхностях [2].

И в данной работе рассматривается применение энергостатического метода определения интегральных характеристик процесса прошивки (основные идеи метода изложены в работах [6–9]) на двухвалковом стане с приводными направляющими дисками (стан Дишера) с учетом ряда допущений.

При определении внешних сил и моментов, действующих в очаге деформации в рассматриваемом процессе, в соответствии с [10] необходимо использовать следующие положения:

• 1)    условие равновесия очага деформации в осевом направлении (равновесие внешних сил);

• 2)    условия равновесия очага деформации в тангенциальном направлении (равновесие моментов внешних сил по отношению к рассматриваемому объему);

• 3)    уравнение баланса мощности Е ; ^ = 0.

Данные положения позволяют определить контактные давления и удельные силы трения, действующие на валки, оправку и приводные диски, а также скорость вращения оправки, сообщаемую ей металлом при прошивке (в случае свободновращающейся оправки).

Согласно [2] уравнения равновесия сил и моментов в осевом и тангенциальном направлениях в установившейся стадии процесса прошивки можно представить в виде

k podS + f T0dS + f$, p^dS’ + f$, T'odS’ + f$„ p"odS" + fs„ T"odS" + Рд = 0,          (1)

где p0, p'o, p"0 - осевые проекции давлений на контактных поверхностях с валками, оправкой и дисками соответственно;

• т₀, т’₀, т"₀ - осевые проекции удельных сил трения на контактных поверхностях с валками, оправкой и дисками соответственно;

• S,    S’, S" - площади контактных поверхностей с валками, оправкой и дисками соответственно;

Р д - дополнительное усилие подпора со стороны заднего конца заготовки.

f MpdS + f MTdS + Js, M'pdS' + fs, M'TdS' + fs„ M”pdS” + Js„ M"TdS" + Мд = 0,     (2)

где M p , M' p , M" p - удельные моменты давления на валках, оправке и дисках соответственно;

M_T, M'_T, М"_т - удельные моменты сил трения на валках, оправке и дисках соответственно;

М д - дополнительный момент, приложенный к заготовке.

На рис. 1–3 представлены схемы действия удельных сил нормального давления и трения на валках, оправке и дисках [2].

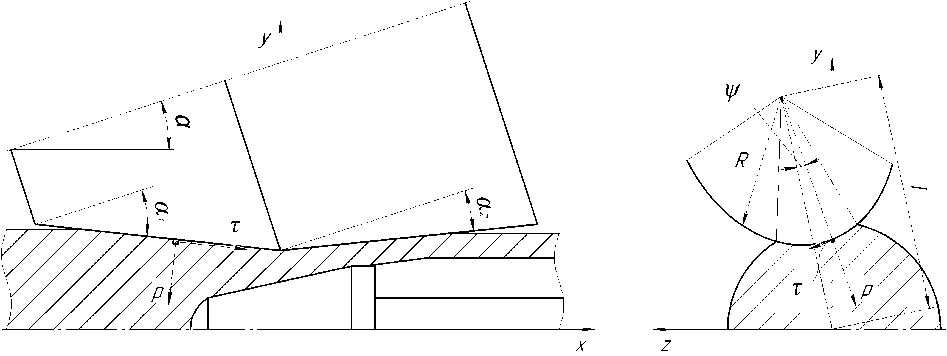
Рис. 1. Схема действия удельных сил на контактной поверхности металла с валками:

a - угол раскатки; а_г,а₂ - углы входного и выходного конусов валка; ^ - угол между кратчайшим расстоянием между осями прошивки и валка I и направлением действия нормального давления, в р ассматриваемом сечении очага деформации основной меридиональной плоскостью заготовки; R - радиус валка

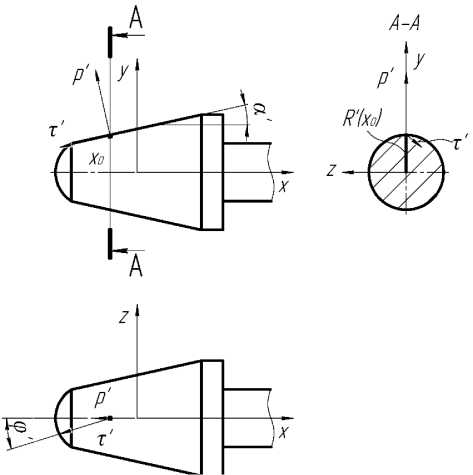
Рис. 2. Схема действия удельных сил на контактной поверхности металла с оправкой: а' - угол конусности рабочего участка оправки; ф' - угол отклонения удельной силы трения от осевого направления; R'(x0) - текущий радиус оправки в рассматриваемом сечении очага деформации

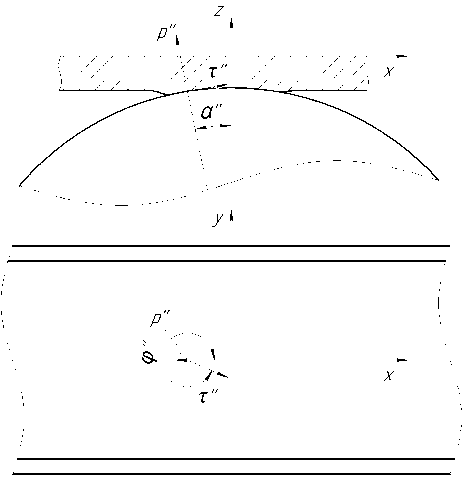
Рис. 3. Схема действия сил на контактной поверхности металла с дисками: а" - угол охвата очага деформации по диску; ф” - угол отклонения удельной силы трения от осевого направления

В соответствии с [2] балан с мощностей в очаге деформации при прош ивке на двухвалковом стане с приводными направляющими дисками представляется в виде

N t + N " = N„ + N ' _T + N" + N ф ,                                                (3)

где N_T - мощность сил трения, подводимая в очаг со стороны валков;

N T' - мощность сил трения, подводимая в очаг со стороны дисков;

N_CT - мощность сил трения скольжения на валках;

N_C ' _T - мощность сил трения скольжения на оправке;

N_C 'T - мощность сил трения скольжения на дисках;

N ф - мощность формоизменения.

В соответствии с [5] распи шем члены уравнения (3) следующим образо м:

• 2 ^(f, V_B)dS + 2 Цф, V^dS = .Ц B V^dS + /_5опр (F, V?) dS + J J Г, ^dS + N ф ,     (4)

где V_B - вектор скорости валка;

• V - вектор скорости диска;

• V_o, V_o, V_o - векторы скоростей скольжения на валках, оправке и дисках соответственно.

Поскольку характер распределения нормальных давлений и удельных сил трения на контактных поверхностях металла с рабочим инструментом при прошивке является достаточно сложным (из-за различного характера истечения металла в зонах очага деформации), для упрощения интегрирования выражений (1), (2), (4) введем допущение – удельные давления и удельные силы трения распределены равномерно в пределах осевого полушага подачи заготовки S_x .

В качестве закона трения на контактной поверхности металла с рабочим инструментом примем закон Амонтона – Кулона, в соответствии с которым

т = f • p,                                                                                              (5)

где т - удельная сила трения;

f - коэффициент внешнего трения;

р - контактное давление.

В соответствии с направлением действия контактного давления и трения в очаге деформации в установившейся стадии прошивки (рис. 1–3), после проецирования их на осевое и тангенциальное направления, используя принятое допущение, а также на основании выражений (1)–(5), получаем следующую систему уравнений равновесия и энергетического баланса:

' ±p b x S x cosP ⁽fcosф x ± tga) - p\S_x b' x tga' x + f 'cosф' x S_x b' x ) ± ±p‘⁽f''S_x b x cos^ x ± S x b’ x tga' x ) = 0;

p [f b_x S_x (IcosM - R_x)sin^_x - b_x S_xIsinw] - p f S_x b'_x R'_xsinф'_x — -p " f "s_x b' x I '' sin^ x ' = 0;

• 2 f p V b x S x cos6 x + 2 f '' p ' V '' S x b’ x cos^ x = f p V O b x S x +

I                +fp Vo^sx b'x + f' p "vOXsxb'X + ^ф, где bx, b'x, b'x - ширины контактных поверхностей металла с валком, оправкой и диском соответственно;

• f, f‘, f" - коэффициенты внешнего трения на валке, оправке и диске соответственно;

• ф _x , ф' х: , ф X - углы отклонения удельных сил трения (сил трения) на контактных поверхностях металла с валком, оправкой и диском соответственно;

• Р - угол подачи;

• a - угол конусности очага деформации по валку;

• a'_x - текущий угол конусности рабочего участка оправки;

• a x' - текущий угол охвата очага деформации по диску;

I - кратчайшее расстояние между осью валка и осью прошивки в рассматриваемом сечении очага деформации основной меридиональной плоскостью валка;

• м - угол основного меридионального сечения по валку;

• I " - расстояние от оси диска до точки действия удельной силы трения на контактной поверхности металла с направляющим диском;

• V, V '' - скорости точек на контактной поверхности валка и диска соответственно;

• V_o, V_o ' , V O' - скорости скольжения металла на контактных поверхностях с валком, оправкой и диском соответственно.

Осевая проекция нормального давления на валке может иметь как положительный (в конусе прошивки), так и отрицательный (в конусе раскатки) знаки. Удельные силы трения на контактных поверхностях металла с валками могут иметь как положительные, так и отрицательные проекции на осевое направление и направления моментов в тангенциальном направлении, в зависимости от характера зон скольжения вдоль и поперек очага деформации.

При использовании раскрутки стержня оправки на контактной поверхности металла с оправкой могут возникать зоны тангенциального отставания. В этом случае проекции удельных сил трения на осевое направление и направление моментов этих сил относительно оси прошивки принимают положительные знаки.

При удержании оправки вдоль всей контактной поверхности с металлом наблюдается зона тангенциального опережения и удельный момент сил трения относительно оси прошивки действует в отрицательном направлении.

При свободно вращающейся оправке, с учетом увеличения ее радиуса в направлении выхода из очага деформации, на контактной поверхности преобладает зона тангенциального опережения и удельный момент сил трения действует в отрицательном направлении относительно оси прошивки.

Характер зон скольжения на контактной поверхности металла с дисками в осевом направлении определяется соотношением частот вращения валков и дисков, а также тянущей способностью валков и условиями вторичного захвата.

При определении мощности формоизменения при прокатке на оправке необходимо учитывать обжатие и утонение стенки гильзы в калибре, образованном валком и оправкой, утолщение во внеконтактной зоне и скручивание в зоне контакта с направляющими дисками. Согласно работе [11]:

Мф = №vHdV, где V - объем очага деформации;

Н - интенсивность скоростей деформации сдвига.

В работе [5], пренебрегая скручиванием на длине полушага подачи заготовки, получили следующую формулу для определения мощности формоизменения

Мф = 2 rs hx $x(in^-ln-^), (7)

л% л1% где т5 - фактическое сопротивление деформации прошиваемого металла;

h_ox, h_x,h_lx - толщины полого тела в геликоидальном направлении очага деформации при входе в зазор между валками, выходе из зазора и входе в зазор через полушаг подачи, с учетом утолщения из-за внеконтактной деформации.

Для определения углов отклонения сил трения от осевого направления на контактных поверхностях металла с рабочим инструментом необходимо выполнить кинематический анализ возможных полей скоростей. Наиболее удобный подход к решению данной задачи изложен в трудах [2]. Авторами проведен обширный анализ векторных полей скоростей металла и инструмента на контактных поверхностях металла с валками, оправкой, направляющими линейками и роликами (направляющие валки), но не сделан анализ на прошивных станах с направляющими приводными дисками (станы Дишера). Используя данный подход, а именно подвижную систему координат с тангенциальным и осевым направлениями, построены возможные векторные диаграммы скоростей на контактной поверхности металла с направляющими приводными дисками, представленные на рис. 4.

На рис. 4а представлена диаграмма скоростей металла и диска в случае осевого отставания, на 4б – в случае осевого опережения.

В соответствии с приведенными диаграммами на рис. 4, угол отклонения силы трения от осевого направления определяется следующим образом:

• ^" = ^ ^{+ arc}tg( "^м ), (8) lj LUd^ m ±/

где ^ = ^V - коэффициент скорости.

V

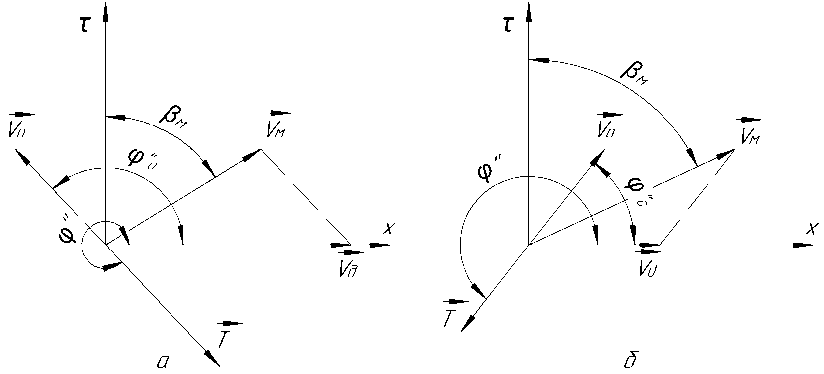
Рис. 4. Векторные диаграммы скоростей на контактной поверхности металла с диском: Р м — угол отклонения вектора скорости металла от тангенциального направления, ф О - угол отклонения вектора скорости скольжения V_o от осевого направления, ф " - угол отклонения вектора силы трения от осевого направления

Полученная система уравнений (6) с учетом (7) имеет шесть неизвестных значений: нормальные давления на валках - р, оправке -р' и дисках - р ", фактическое сопротивление деформации - т₅, угол отклонения силы трения от осевого направления на контактной поверхности металла с оправкой - ф , , скорость скольжения металла на контактной по-верхностис оправкой - У_о.

При использовании раскрутки стержня можно определить скорость в любой точке контактной поверхности на оправке. В этом случае величина ф , становится известной и определяется в соответствии с [2] как

• ф, = л + arttg^M^^        (9)

где р' = ^ М - коэффициент скорости;

У м - скорость на контактной поверхности металла с оправкой;

• У - скорость точки на контактной поверхности оправки.

В случае неподвижной оправки угол ф , =       .

Для свободно вращающейся оправки определить угол ф , , используя представленные выше выражения, нельзя. В этом случае для сокращения количества неизвестных в системе (6) можно воспользоваться связью между скоростью оправки и скоростью скольжения металла на контактной поверхности с ней [2]:

Уо = 7(У sinPм)2 + (Ум cos^ -У' )2. (10)

Для решения данной системы дополнительно можно использовать выражения для определения нормального давления на валках и фактического сопротивления металла пластической деформации.

В работе [12] описано несколько вариантов определения нормального давления металла на валки при прошивке, в зависимости 2г от отношения —, где г - радиус заготовки, b - ширина контактной поверхности металла с валком в рассматриваемом сечении очага деформации.

2г

В диапазоне 1 < — < 8,5 нормальное давление определяется следующей зависимостью [13]

р = 2 ts (1,25 1п2Г+ 1,25 ^-1,25). (11)

2г

При — > 8,5 нормальное давление определяется формулой Прандтля

р = 2 rs (1 + ^).                      (12)

2г

Для случаев, когда отношение — > 1, в работе [14] получена формула

р = (3,92 - 4,62) ts. (13)

Для определения фактического сопротивления деформации прошиваемого металла можно использовать многочисленные труды ученых и специалистов [16, 17].

Таким образом, с учетом (7)–(13) можно решить систему (6) относительно трех неизвестных значений: нормальных давлений металла на оправку и диски и скорости оправки.

Полученная система уравнений равновесия и энергетического баланса очага деформации процесса прошивки на двухвалковых станах поперечно-винтовой прокатки с направляющими приводными дисками позволяет определить характер распределения нормальных давлений и удельных сил трения на направляющих дисках и оправке, а также определить скорость оправки в установившемся режиме прошивки в случае использования свободновращающейся оправки. Используя полученные распределения нормальных давлений и удельных сил трения на контактных поверхностях металла с рабочим инструментом, можно определить полные усилия и вращающие моменты, действующие на валки, оправку и диски.