Применение эрмитового биквадратного конечного элемента

Билинейные конечные элементы на прямоугольниках давно и успешно используются для решения двумерных стационарных и нестационарных задач [1–3]. C помощью аффинных, изопараметрических и других преобразований область их применения расширена до широкого круга двумерных областей, в том числе с криволинейной границей [1; 3–6]. Однако точность аппроксимации этими конечными элементами невысока: второй порядок в L2 -норме и только первый в H1 -норме. Поэтому интенсивно развились конеч- ные элементы с базисными функциями-многочленами более высокой степени, обеспечивающими и более высокий порядок аппроксимации.

Причем развитие шло в направлении как лагранжевых, так и эрмитовых элементов. Сопоставление двух типов элементов дает основание утверждать о бóльшей эффективности эрмитовых элементов по сравнению с лагранжевыми элементами ввиду меньшей размерности порождаемых систем дискретных алгебраических уравнений при равных свойствах аппроксимации [7]. Более того, для некоторых эрмитовых элементов достигнута не только межэлементная непрерывность, но и межэлементная C'-гладкость, включающая непрерывность первых (частных) производных [1; 8; 9].

Поэтому повышение интереса к эрмитовым конечным элементам остается актуальным. Вместе с тем описанная в литературе линейка эрмитовых элементов начинается с бикубических элементов и продолжается только по нечетным степеням.

В этой статье мы опишем двумерный эрмитов элемент второй степени на прямоугольнике, начинающий линейку эрмитовых конечных элементов.

Описание элемента. Сначала, используя терминологию работ [1; 2], построим референтный элемент ( e, P - , 5 e ) как тройку, состоящую из ячейки e , пространства функций P e и множества степеней свободы 5 e . В качестве референтной ячейки возьмем единичный квадрат e = [0,1] х [0,1] с четырьмя вершинами С = (1,1), а 2 = (1,0), а ^ = (0,0), о , = (0,1) (рис. 1).

у1

(однозначной разрешимости) пары ( P e , 5 _e ) достаточно построить базис Лагранжа {ср _i j ( 5c, y) e P e , j = 1,2, i = 1,...,4} на e, удовлетворяющий условию [1]

V i , j (Ф k , i ) = ⁵ i , k ⁵ j,i ,                         ⁽³⁾

где 5 _{i k} - символ Кронекера.

Прямая проверка показывает, что базис Лагранжа имеет следующий вид:

$ 1,1 = xy >(1 ^- x + ^y),

$ 2,1 = ^{x (1 -} y ⁾⁽ x + Я $ 3,1 = (1 - x )(1 - y )(1 + x - y), $ 4,1 = ^{(1 - x ) y (2 -} x ^{- y)},

$ 1,2 = xy(x ^- 1), $ 2,2 = ⁵y ^{(1 -} Я ⁽⁴⁾ $ 3,2 = ^{x (1 - x )(1 -} Я $ 4,2 = ^{(1 - x ) y(}У ^{- 1)}.

Для проверки интерполяционных свойств этого элемента используем обычные обозначения для пространств Соболева. Пусть Р .₂( О ) - гильбертово пространство функций, измеримых по Лебегу в области Q , со скалярным произведением

( u , v ) _Q = J _Q uvd Q , u , v e Р 2 ( О ) и конечной нормой

II ^u l1о,П = ⁽ u ’ u^ u ^{e L} 2^{( Q )} .

3 3 I                   4 4»

0                     1 (

Рис. 1. Референтная ячейка

Мы определим пространство функций P_e как линейную оболочку восьми полиномиальных одночленов:

P e = span { 1, x, y, xc², xcy, y², x²y, 5cy ²},       (1)

а множество степеней свободы 5 e складывается из значения функции и одной из частных производных в каждой вершине квадрата:

⁵ e = { w i ,1 ^{( p)} = ^{p (} a i X i = Х-Л

V i ,2 ( P ) =d P(a i )/dx, i = 1,3,                    ⁽²⁾

V i ,2 ( P ) = d p(a i )/d y , i = 2,4, p e P - } .

Отметим, что каждой вершине соответствуют две степени свободы, но направления производных различны в вершинах с четными и нечетными номерами. Покажем, что этот набор действительно является корректным конечным элементом в смысле монографии [1].

Лемма 1 . Тройка ( e , P_e , 5 _e ) представляет собой конечный элемент.

Доказательство . Размерность пространства P_e совпадает с количеством элементов множества 5 _e . Поэтому для доказательства унисольвентности

Для целого неотрицательного k обозначим через H^k ( Q ) гильбертово пространство множества функций u e L ₂( Q ), слабые производные которых тоже принадлежат L ₂( Q ) до порядка k включительно. Норма в этом пространстве определяется формулой

I k ,Q

Г . X, 0< s + r < k

ds+ru dxf dx2

2 A1/2

0,Q J

Введем также полезную полунорму

k ,Q

Г

X, s+r=k

d ^{s +} r u d x ^f d x ^rr

2   A1/2

0,Q J

u e H^k ( Q ).

Пусть й - произвольная функция из H ³ ( e). По теореме вложения пространств Соболева H ³ ( e ) непрерывно вложено в C 1 ( e ) [10], поэтому й e C ' ( e ). В итоге мы можем построить интерполянт u I e P_e :

4 2

^u I ^{( x}1 , ^x2 ) = EX' ¹ i , j ^(ZC)( P / , j ⁽ x ! , x 2) .

i =1 j =1

Теорема 1 . Пусть й e H ³ ( e ). Тогда для любого целого m < 3 справедлива оценка

14$^- 4$ im , e <  c 1 H, e                     ⁽⁶⁾

с константой c 1 , не зависящей от й.

Доказательство . Максимальный порядок частных производных в определении множества 5 _e равен

единице. А как уже упоминалось, пространство H ³ ( е ) вложено в C ' ( e ). Кроме того, из (1) следует, что P - з P ₂( e), где P₂(e ) - пространство многочленов суммарной степени не выше двух. Таким образом, выполнены все условия теоремы 3.1.5 в монографии [1], из которой и следует оценка (6).

К этому конечному элементу возможно применение аффинных и изопараметрических преобразований для аппроксимации границы области [1]. Поскольку вдоль границы ячейки базисные функции являются квадратичными, то они предоставляют возможность более точной аппроксимации границы, чем билинейные или линейные элементы.

Вместе с тем из-за неоднородности степеней свободы для этого элемента полезно использовать еще одно простое преобразование. Для иллюстрации его необходимости рассмотрим разбиение области Q = (0,1) х (0,1) на элементарные квадратные ячейки (рис. 2), проведя два семейства параллельных прямых x i = ih , i = 1, ..., n - 1, и y j = jh , j = 1, ..., n - 1, с шагом h = 1/ n .

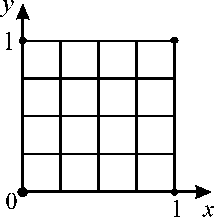
Рис. 2. Разбиение прямоугольника на элементарные ячейки

Обычное преобразование референтного элемента на элементарную ячейку выглядит следующим образом:

x = x i + hx , У = y j ^{+ hy} .

Рассмотрим две соседние элементарные ячейки в разбиении исходной геометрической области (рис. 3). При использовании преобразования вида (7) (рис. 3, a ) получается рассогласование степеней свободы в общих узлах соседних элементов. В принципе, можно ввести формулы пересчета производных из одного элемента в другой. Но это усложнит реализацию метода. Поэтому мы введем еще одно простое преобразование:

x = x i + hy , y = y j + hx .

Применяя его в одном из соседних элементов, мы получим совпадение степеней свободы в узлах сетки (рис. 3, б ).

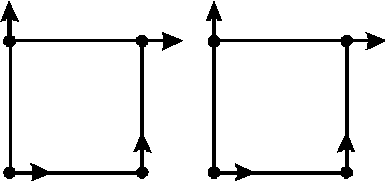
(7)                      (7)

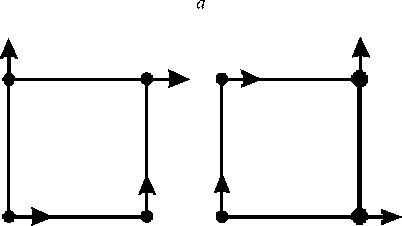
(7)                     (8)

б

Рис. 3. Соседние ячейки с одинаковыми и разными преобразованиями: а - одинаковые преобразования;

б - разные преобразования

Итак, предложенный эрмитов биквадратный конечный элемент имеет 8 степеней свободы в каждой элементарной ячейке, а каждому узлу ( x i , y j .) соответствует комбинация всего двух базисных функций ф i j и ф ij , которые строятся следующим образом.

Базисная функция ф i j принимает значение 1 в узле ( x i , y j ) и 0 в других узлах сетки так же, как и ее производные дф ij ( x_k , y, ) ]дх = 0 в узлах с четной комбинацией k + I и дф ij ( x_k , y , ) [дy = 0 в узлах с нечетной комбинацией k + I .

Базисная функция фij равна нулю во всех узлах сетки. Но при четной сумме i + j ее производная по x дф ij (xk, y,) /дx принимает значение 1, если k = i и I = j, и 0 во всех остальных узлах с четной суммой k +1, а ее производная по y дф ij (xk, y,) [дy обращается в нуль во всех узлах с нечетной суммой k +1. А при нечетной сумме i + j ее производная по y дф ij (xk, y,) [дy принимает значение 1, если k = i и I = j, и 0 во всех остальных узлах с нечетной суммой k + ,, а ее производная по x дфij(xk,y,)/дx обращается в нуль во всех узлах с четной суммой k +,. В итоге базисные функции имеют следующий вид. Для узла с четной комбинацией индексов i + j sh

Ф i , j

( x +i - x ) ( y j +1 - у ) ( h y ( x - x i )⁺ h x ( y j +1 - y ) )/ h x h y ( x - х -i ) ( y j +i - y ) ( h y ⁽ x - x ) ⁺ h x ( j - y ) ) [hy h y ■ ( x +i ^{- x} ) ( У ^- y j -i ) ( h y ^{( x - x}d ⁺ h x ( У ^- y j -i ) )/ h x h y ( x - х -i ) ( у - y j -i ) ( h y ( x - x )⁺ h x ( у - y j -i ) ) Ih x h y

при при при при

^{( x} , y ) g [ x i ,x i +i ] ^{( x} , У ) g [ x -i , x ] ^{( x} , У ) g [ x , x +i ] ^{( x} , У ) g [ x -i , x ]

^x L y j , y j +i

^x L y j , y j +i

^x L y j -i , y j ^x y j -i , y j

иначе;

	( x - x i )( x i +i -( x - x i )( x - x i		x )( y j +i - У V h x h y		при при	( x , У ) е [ x i , x i +1 ] x ( x , У ) e [ x i -1 , x i ] x	= y j , y j +i = = y j , y j +i =
			-i )( y j +i -	У )/ h x h y
v tj = ■	( x -	x i )( x i +i -	x )( У - y j	- i )/ h x h y	при	( x , У ) e [ x i , x i +i ] x	= y j-1 , y j __
	( x -	xi )( x - xi	-i )( У - Уj	- l)/ h x h y	при	( x , У ) e [ x i -1 , x i ] x	_ y j -i , y j _
		0				иначе;

а для узла с нечетной комбинацией индексов i + j

	( x +	- x )c y j +1	- У )С h y С x i - x ) + h x	( У - У	-i ))/ h x h y 2	при	( x , У ) e [	x i , x i +i	x	= y j , y j+i =
	( x -	x i -i )c y j +1	- У )С h y С x - x i ) + h x	( У - У	-i ))/ h x 2 h y 2	при	С x , У ) e [	x i -i , x i	x	= y j -, y j +i =
Ф shj =	( x,+	- x )С У - Уj -1 )( h y ( x i - x ) + h x		( y j +i -	У ))/ h x h y 2	при	( x , У ) e [	x i , x i +i	x	= y j -1 , y j =
	( x -	x i -1 )С У - y j -i )( h y ( x - x i ) + h x		( y j +i -	У ))/ h x h y 2	при	( x , У ) e [	x i -i , x i	x	_ y j -i , y j _
			0				инач
	"c y -	У j )c x i +1 -	x )( y j +1 - У V h x h y	при	( x , У )e [ x ,	x +i ] x	= y j -, y j+i =	,
	( У -	y j )c x - x i	-i )c y j +1 - У )/ h x h y	при	( x , У )e [ x -	i , x i ] x	= y j -, y j +i =	,
v j =■	С y -	У j )c x i +i -	x )С У - y j -i)/ h x h y	при	( x , У )e [ x ,	x +i ] x	=y j -i , y j_	,
	С y -	y j )c x - x i	-1 )С У - y j -1V h x h y	при	( x , У )e [ x -	i , x i ] x	_ yj -i , y j _	,
		0			иначе.

Численный пример. Проиллюстрируем свойства предлагаемого конечного элемента на следующем примере. Пусть Q = (0,1) x (0,1) - квадрат (см. рис. 2)

с границей Г. Рассмотрим краевую задачу

5^ ди^ 5^ ди^

--I Ц— I--1 Ц— 1 = f в ^, дx V дx ) ду V ду )

0 при x = 0, и (x, У ) =

0 при у = 0,

- у sin у при x = 1, на Г

- x sin x при y = 1, с правой частью f (x, y) = 2 (x + x2 + y + 3 xy + y2) cos (1 - x - y) +

+ (-У + 2x y + x (-1 + 2y + 2y )) sin (1 - x - y)

и коэффициентом ц ( x , y ) = x + y +1. Точным решением этой задачи является функция

u ( x , y ) = xy sin (1 - x - y ).

Разделим область Q на элементарные квадраты, проведя два семейства параллельных прямых xi = ih, i = i, ..., n -i, и yj = jh, j = 1, ..., n -1, с ша гом h = I/ n.

Для выяснения порядка точности при уменьшении размера сетки построим систему линейных алгебраических уравнений методом конечных элементов с использованием базисных функций (9)-(I2) для n = 10,20,40. Поскольку точное решение априори известно, то разность и - u_h между точным и приближенным решением можно выразить в явном виде. Рассмотрим следующие нормы - дискретные аналоги норм в L и H ¹:

II ^{и -} u h | |_{0 h} ⁼ Е ( ^{и ( x} i , y j ) ^- u h ^{( x} i , у j ) ) ^{h 2} , ’      i< i <  n -i, i< j <  n -i

||^{u -} u h li _h = Е      ( ^{u (} x , y j ) ^- u h ⁽ x , y j ) ) ^{2 h 2 +}

’     i< i <  n -i,i< j <  n -i

+ Е     (ди/дx(xi,yj)-дuh/дx(xi,yj-)) 2h2 + i

⁺ Е      ( ^{д и} /^д y ^{( x}v y j ) ^{-д uh} /^д у ⁽ x , y j ) ) ² 2 ^{h 2} .

i< i < n -i, i< j < n -i i + j - нечетные

Напомним, что используемые в них значения производных совпадают со степенями свободы и не требуют дополнительных вычислений или аппроксимаций.

Точность приближенного решения

h	δ h = u - uh II0, h	σ h = u - uh II1, h	δ 2 h /δ h	σ 2 h /σ h	log 2 (δ 2 h /δ h )	log2(σ2 h /σ h )
0,1	1,15 × 10 - 6	0,00084	14,7 15,4	3,5 3,7	3,88 3,94	1,8 1,9
0,05	7,8 × 10 - 8	0,00024
0,025	5,07 × 10 - 9	6,48 × 10 - 5

Отметим, что с теоретической точки зрения для достаточно гладкого решения задачи гарантируются следующие порядки точности.

Теорема 2. Пусть u∈H3(Ω). Тогда справедливы оценки u-uh Ω ≤ c2h2 IIuII 3,Ω (13) и u-u0,Ω ≤c3hIIuII 3,Ω (14) с константами c2и c3, независящими от u и h.

Доказательство . Оценка (13) получается стандартным образом [1; 2; 6] из теоремы 1 путем масштабирования и применения к совокупности элементарных квадратов. А оценка (14) вытекает из нее на основании приема Нитше [1; 2].

То есть в нашем примере мы должны получить второй порядок сходимости в норме H ¹ и третий порядок в норме L ₂. А практически для дискретных аналогов получаем следующее (см. таблицу).

Что касается поведения погрешности σ h ⁼ II u - u^h II , то ее порядок действительно близок к двум. А вот погрешность δ _h = II u - u^h II ведет себя гораздо лучше теоретически предсказанного третьего порядка, демонстрируя близость к четвертому порядку. Это объясняется следующим образом. Оценки (13) и (14) справедливы, вообще говоря, на неравномерных сетках. На неравномерной сетке погрешность в дискретной среднеквадратичной норме действительно будет лишь третьего порядка малости. Но что касается равномерной сетки, то получающаяся конечноразностная схема имеет симметричный шаблон и потому не может быть нечетного порядка точности ввиду сокращения нечетных степеней в разложении Тейлора для погрешности аппроксимации. Поэтому после сокращения слагаемых третьего порядка аппроксимации остаются лишь слагаемые четвертого порядка малости, которые и определяют четвертый порядок сходимости для дискретного набора значений. Но при вычислении (недискретной) нормы II u - u^h II _Ω она оказывается лишь третьего порядка, как и предсказывается теоремой 2.

Итак, в статье представлен новый эрмитов биквадратный элемент на прямоугольнике. До сих пор эрмитовым конечным элементом наименьшей степени был бикубический элемент. Поскольку биквадратный элемент проще бикубического, то для решений класса H ³ ( Ω ) он оказывается более экономичным.

Относительно неожиданным свойством оказался его повышенный порядок точности в дискретной среднеквадратичной норме на равномерной сетке . Вместо третьего получается четвертый порядок точности. Это объясняется симметрией шаблона получающейся конечно-разностной схемы. В итоге, в этой дискретной норме на равномерной сетке порядок точности биквадратного и бикубического элемента совпадают, что делает первый элемент более предпочтительным ввиду меньшего числа степеней свободы и более простой структуры дискретных уравнений.