Применение коэволюционного алгоритма генетического программирования в задаче аппроксимации рефрактометрических свойств оптически прозрачных кристаллов

Высокие темпы информатизации привели к тому, что в настоящее время появилась возможность компьютерного моделирования и проектирования сложных систем, изучения их свойств и управления ими в условиях неполноты информации, ограниченности ресурсов, дефицита времени. Однако для исследования характеристик любой системы математическими методами должна быть обязательно выполнена формализация, т. е. построена математическая модель. Исследования с помощью математических моделей зачастую являются единственно возможным способом изучения сложных систем и решения важнейших задач управления. Так, например, обстоит дело при изучении процессов, протекающих в течение длительного времени, – в условиях математического моделирования подобный процесс может быть исследован в ускоренном масштабе времени.

Однако на практике сложно зафиксировать свойства функциональной зависимости выходных величин от входных и еще сложнее привести аналитическое описание такой зависимости. Если экспертные знания об объекте в явном виде отсутствуют, то обычно по имеющимся статистическим данным строится некоторая вычислительная модель. Однако недостаток численной модели при всем ее удобстве для принятия решений заключается в том, что она, по сути, является «черным ящиком», т. е. моделью, в которой перечисляются входные и выходные связи системы со средой, а информация о внутренней структуре полностью отсутствует.

Решение задачи символьной регрессии могло бы значительно улучшить сложившуюся ситуацию. Символьная регрессия дает нам не только вычислительную процедуру, но и математическое выражение в символьной форме, которое можно подвергнуть содержательному анализу, упростить и уточнить. Один из самых многообещающих подходов в данном направлении – это генетическое программирование [1]. Алгоритм генетического программирования является модификацией генетического алгоритма [2]. Основное различие заключается в представлении решений. Решения в генетическом программировании могут иметь различную форму и размер, наиболее распространенное представление – это представление в виде деревьев.

При решении задачи символьной регрессии алгоритмом генетического программирования в качестве функции пригодности используют нормированную на области значений выходной зависимой переменной ошибку аппроксимации, вычисленную с использованием какой-либо метрики, например евклидовой, Миньковского и др.

Алгоритм генетического программирования, как и генетический алгоритм, является стохастической процедурой, оценка его эффективности (надежности) осуществляется усреднением количества найденных решений по многократным запускам. Однако нельзя однозначно сказать о превосходстве определенного алгоритма, но можно выявить (по большинству лучших результатов) наиболее эффективный алгоритм и проранжировать остальные алгоритмы в порядке убывания показателя надежности [3].

Но даже после многократных решений поставленной задачи остается неопределенность в выборе параметров настройки алгоритма генетического программирования. Это подтверждает тот факт, что для каждой задачи существует свой наилучший алгоритм, т. е. своя стратегия поиска решения. Также следует отметить, что не всегда имеется возможность многократного запуска алгоритма для нахождения более точного решения по многим причинам, например из-за высокой стоимости вычислений целевой функции, отсутствия времени на перезапуск алгоритма и т. д.

Поэтому необходимо выбирать конкретный алгоритм и настраивать его параметры на решаемую задачу исходя из какой-либо априорной информации или из накопленного опыта. Но выбор конкретного алгоритма и настройка его параметров сами по себе являются очень сложными задачами, при неудачном решении которых алгоритм может не справиться с поставленной перед нами целью [4].

Коэволюционный алгоритм генетического программирования. Одним из методов разрешения проблемы выбора эффективной стратегии поиска для задачи символьной регрессии с помощью алгоритма генетического программирования является использование коэволюционной стратегии, т. е. конкуренции алгоритмов за вычислительные ресурсы.

Основная идея коэволюционного алгоритма генетического программирования (КАГП) состоит в следующем: одновременно эволюционируют несколько субпопуляций в рамках индивидуальных алгоритмов генетического программирования, каждый из которых обладает своей стратегией поиска и самостоятельно решает поставленную задачу [5; 6]. При этом алгоритмы борются за общий вычислительный ресурс, который в течение работы коэволюционного алгоритма перераспределяется в пользу более эффективного из них через заданный интервал адаптации, выраженный в количестве поколений.

Поскольку коэволюционный алгоритм основывается на конкурирующих стратегиях алгоритмов генетического программирования, то для субпопуляций необходимо ввести функцию пригодности. С помощью этой функции определяется лучшая популяция и ей дается больше ресурса для решения задачи. Пусть Т – интервал адаптации, b ( k ) = ( k T , k T– 1 , …, k 1 ) – вектор длиной Т . Если i- я популяция в момент k содержит наилучшего (по всем популяциям) индивида, то b i ( k ) = 1, иначе b i ( k ) = 0. Качество популяции можно оценить по формуле [7]:

Т - 1 T _- k q_i = ∑        ⋅ b_i ( k ).               (1)

k = 0 k ⁺ 1

Изменение размера ресурсов происходит путем сокращения субпопуляции каждого проигравшего алгоритма на некоторый процент (определенный заранее) и увеличения субпопуляции победившего алгоритма на число, равное сумме потерь проигравших алгоритмов. Каждому из алгоритмов гарантирован некоторый заранее определенный размер субпопуляции, который не может быть уменьшен, называемый социальным минимумом. Таким образом, общий ресурс, выделенный для решения задачи, остается неизменным. После перераспределения ресурса алгоритмы продолжают свою работу с субпопуляциями, в которые входят только лучшие решения из предыдущих субпопуляций. Процесс продолжается до тех пор, пока либо не выполнится критерий останова, либо не кончится ресурс, выделенный на решение задачи [7].

Задача аппроксимации рефрактометрических свойств прозрачных магнетиков. В оптически прозрачных кристаллах Rb2MnCl4 и NaMnCl3 при низких температурах (ниже 56 и 6,5 К соответственно) устанавливается антиферромагнитный порядок магнитных моментов ионов марганца. Кристаллическая структура первого кристалла (симметрия D4h17) слоистая, расстояние между магнитными ионами в слоях и межслоевое расстояние сильно различаются, поэтому кристалл является магнетиком с почти идеальной двумерной магнитной структурой, позволяющей проводить модельные оценки магнитных свойств, и легкоосным антиферромагнетиком с осью легкого намагничивания, направленной вдоль оси симметрии С4. Второй кристалл также обладает слоистой кристалли- ческой структурой (симметрия R3 ), но его меж- и внутрислоевой обмены близки по величине и различны по знаку. Магнитная кристаллографическая анизотропия у NaMnCl3 типа «легкая плоскость». Из-за большого числа различающихся обменных параметров, определяющих магнитную структуру, расчет магнитных и магнитооптических свойств данного кристалла весьма проблематичен.

В этих кристаллах экспериментально изучались зависимости магнитного линейного двупреломления света (МЛД) от температуры [8; 9]. Для полученных результатов строилась аппроксимация с помощью коэволюционного алгоритма генетического программирования.

При решении задачи использовались следующие параметры коэволюционного алгоритма генетического программирования: терминальное множество – { x , C }, где x ∈ R , C ∈ [–10;10]; функциональное множество – {+, –, *, ÷, sin, cos, sqrt, power, ln, exp}; размер ресурса – 400; начальная глубина деревьев – 3; интервал адаптации – 5; размер штрафа – 10 %; размер социального минимума – 10; количество индивидуальных алгоритмов – 4.

Двупреломление света в Rb2MnCl4. Анализ температурной зависимости линейного двупреломления (ЛД) Rb₂MnCl₄ (рис. 1) показывает, что свет распространяется перпендикулярно оси кристалла C 4 , длина волны света λ = 632,8 нм. Однако отсутствие дополнительных сведений о коэффициентах расширения и магнитострикции кристалла не позволяет выделить магнитный вклад в ЛД. Аномальное изменение ЛД при температурах ниже 200 К можно связать с наличием в кристалле магнитного порядка и считать, что температурная производная ЛД d Δ n/dT (рис. 2) представляет собой лишь незначительно искаженную производную магнитного вклада в Δ n .

Согласно общему выводу феноменологический теории, ЛД должно быть пропорционально второй степени компонент антиферромагнитного вектора или, в случае коллинеарного двухподрешеточного антиферромагнетика с малой анизотропией, квадрату подрешеточной намагниченности. Однако сравнение температурного хода ЛД с температурной зависимостью квадрата намагниченности подрешеток показывает их существенное расхождение в окрестности и выше темперетуры Нееля T N . Если подрешеточная намагниченность в окрестности T N быстро убывает и обращается в нуль, то магнитный вклад в ЛД существует при температурах, значительно превышающих T N . Последнее указывает на большую величину среднеквадратичных флуктуации вектора l в парамагнитной фазе, отражающую влияние ближнего магнитного порядка и являющуюся следствием низкой размерности магнитного порядка кристалла.

Для более наглядного определения влияния низкой размерности магнитного порядка ЛД можно описать в терминах, зависящих от спинов поляризуемо-стей ионов.

Полная поляризуемость кристалла, зависящая от спинов, имеет вид

— — *

А П т = A £ ( S j )²} + B £ (( S j S 1 )),        (2)

jj,l где A и B – константы, связанные соответственно с величиной одно- и двухионных поляризуемостей кристалла; Szj – проекция на ось z спина Sj, расположенного на j-м узле.

Из (1) следует, что если одноионные поляризуемости малы по сравнению с двухионными, то А n_m пропорционально магнитной энергии кристалла, а d А n m/ dT ~ c m . Оценить зависимость c m ( T) при высоких температурах можно, используя высокотемпературное разложение в ряд по степеням x = J ( kk_BT ) , где J – обменный параметр; k B – константа Больцмана. Для этого нужно пренебречь межплоскостным обменом и рассматривать высокотемпературное разложение c m для плоской квадратной решетки.

Минимизируя ( d А n/dT ) _КАГП

— ( d ^А ”/d^T ) мод| 12

по

параметру внутрислоевого обменного взаимодействия между ионами марганца J , можно получить его оценку. Такая минимизация дает значение J/k_B = - 5,66 К.

Однако между экспериментальным и модельным результатами, представляющими высокотемпературное разложение, существует значительное различие (рис. 3). Намного лучше аппроксимирует экспериментальные точки зависимость, полученная с помощью коэволюционного алгоритма генетического программирования (сплошная жирная кривая на рис. 2–4).

Нижняя кривая на рис. 2 представляет разницу между модельной зависимостью, определенной для плоской квадратной решетки, и аналитическим выражением, полученным коэволюционным алгоритмом генетического программирования. Эта разница может быть использована для интерпретации несовпадения модельного описания и эксперимента, поскольку она включает в себя неучтенный решеточный вклад, т. е. вклад, связанный с отступлением от двумерного порядка в магнитной подсистеме и т. д.

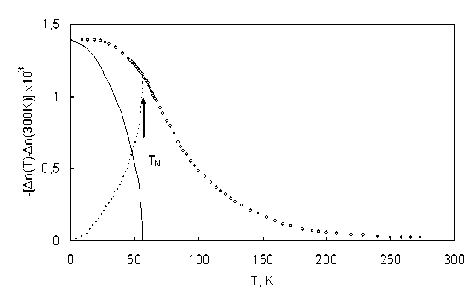
Рис. 1. Температурное поведение Аn Rb2MnCl4: сплошная кривая – ход кривой квадрата подрешеточной намагниченности

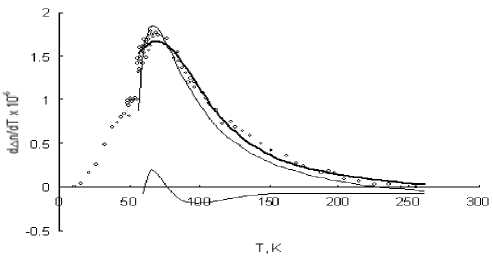
Рис. 2. Зависимость d А n/dT Rb₂MnCl 4 от температуры: сплошная тонкая кривая соответствует высокотемпературному разложению c m (магнитной теплоемкости) для J/k = - 5,66 К; сплошная жирная кривая – аппроксимация, полученная коэво-люционным алгоритмом генетического программирования;

нижняя кривая – различие модели и аппроксимации

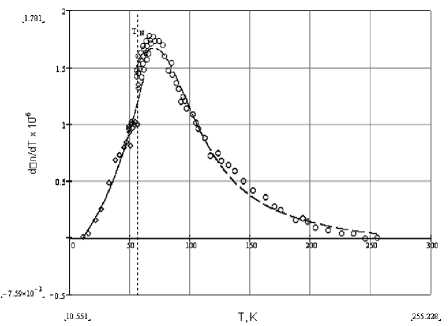
Рис. 3. Зависимость d А n/dT Rb₂MnCl 4 от температуры до (◊) и после (○) фазового перехода: ---и — - результат работы алгоритма

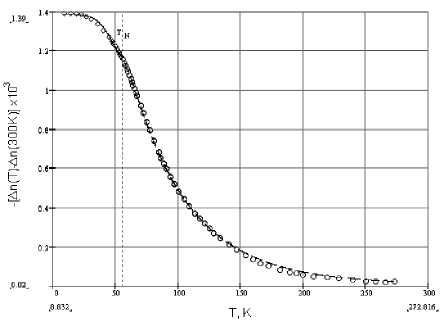
Рис. 4. Температурное поведение А n Rb₂MnCl₄ до (◊) и после (○) фазового перехода: ---и — - результат работы алгоритма

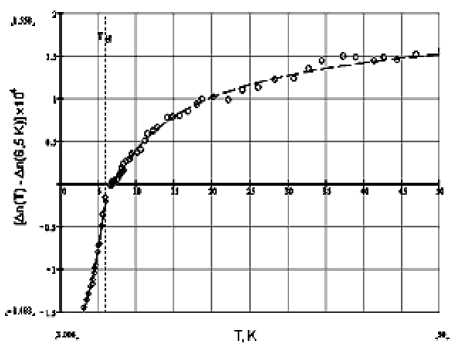
Рис. 5. Температурная зависимость линейного двупреломления света в NaMnCl 3 до (○) и после (◊) фазового перехода (длина световой волны λ = 632,8 нм):

- –– и – – – результат работы алгоритма

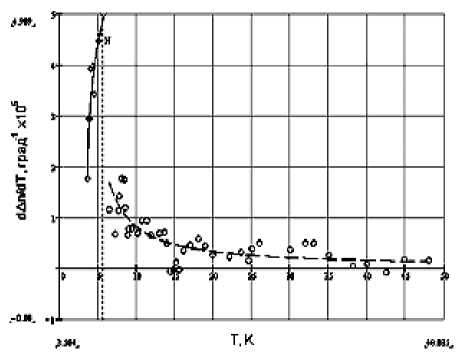
Рис. 6. Температурная зависимость производной линейного двупреломления NaMnCl3 до (○) и после (◊) фазового перехода:

- –– и – – – результат работы алгоритма

Двупреломление света в NaMnCl3. Результаты измерений линейного двупреломления Δ n NaMnCl₃, приведенные к T = 6,5 К (рис. 5), показали следующее.

Поскольку температура Дебая NaMnCl 3 значительно превышает T N , то можно считать, что вклад в Δ n за счет расширения решетки мал. Тогда изменение Δ n при низких температурах ( Т < 50 К) будет обязано только магнитному вкладу, в том числе и стрик-ционному, и изменение Δ n ( T ) можно считать магнитным двупреломлением Δ n_m .

При T N = 6,5 К на кривой Δ n m ( T ) наблюдается излом, который соответствует установлению в кристалле магнитного порядка. Ниже T_N происходит аномально быстрое изменение Δ n , связанное с ростом подрешеточных намагниченностей. При T >  T_N на кривой Δ n ( T ) появляется хвост, который тянется до температур Т ≈ 40 К и обязан ближнему магнитному порядку в кристалле – долгоживущим флуктуациям вектора l .

Принимая во внимание пропорциональность Δ n m магнитной энергии кристалла, а следовательно, и ( d Δ n_m dT ) ≈ c m , проанализируем особенности поведения d Δ n_m IdT NaMnCl₃ (рис. 6). Для этого сравним ее с поведением теплоемкости c m , рассчитанной для слоистых магнитных систем с различным внутри-и межплоскостным обменом.

Для NaMnCl₃ получаем, что c_m ≈ T ³ при T << 3 К, а при более высоких температурах ( T <  T N ) c m ≈ T . При T N кривая d Δ n_m /dT имеет острый максимум, характерный для трехмерных гейзенберговских анти-ферромагнетнетиков. При T >  T_N d Δ n_m /dT имеет вид, отличный от поведения c m двумерных систем (например, Rb 2 MnC 4 ).

Учитывая симметрию кристалла и феноменологические особенности магнитной структуры, получим выражения для компонент симметричного тензора диэлектрической проницаемости εij , описывающие рефрактометрические свойства кристалла:

ε =ε ⁰ + 2 λ l ² + 2 λ l ² + 2 λ ll + 2 λ ll + xx xx                    z z y          z x

+ 2 λ₁₁ ( l_x ² + l_y ² ) ++ 2 ρ ₂ m ² + 2 ρ₄ m_z ² + 2 ρ₉ m_zm_y +

+ 2 ρ₁₀ m_zm_x + 2 ρ₁₁ ( m_x ² + m_y ² ),

ε yy = ε ⁰ yy + 2 λ 2 l ² + 2 λ 4 l z ² - 2 λ 9 l z l y - 2 λ 10 l z l x -

- 2 λ₁₁ ( l_x ² + l_y ² ) + 2 ρ ₂ m ² + 2 ρ₄ m_z ² - 2 ρ₉ m_zm_y -

- 2 ρ₁₀ m_zm_x - 2 ρ₁₁ ( m_x ² + m_y ² ),

ε _zz = ε ⁰ _zz + 2 λ₁ l ² + 2 λ₃ l_z ² + 2 ρ ₁ m ² + 2 ρ₃ m_z² ,

ε =λl2l2+λll+λ (l2-l2)-2λll+ yz 5z y 6z x 7x y 8x y (3) +ρ5mzmy+ρ6mzmx+ρ7(mx2-my2)-2ρ8mxmy,

ε =λ l ² l ² -λ ll +λ ll + 2 λ ( l ² - l ² ) + xz z x z y x y          x y

+ρ5mzmx-ρ6mzmy+ρ7mxmy+2ρ8(mx2-m2y), εxy =2λ9lzlx -2λ10lzly +4λ11lxly +2ρ9mzmx --2ρ10mzmy+4ρ11mxmy, где ε0ij – значения диагональных компонент тензора диэлектрической проницаемости в парамагнитной фазе; λ и ρ – магнитооптические коэффициенты.

Выражения (3) полностью описывают состояние оптической индикатрисы кристалла в магнитоупорядоченной фазе. Однако теоретически рассчитать температурное поведение λ и ρ невозможно, поскольку выражения (3) описывают влияние дальнего порядка на εij. Получить флуктуационный вклад в парафазе из модельных соображений также нереально, так как магнитная система имеет сложную структуру и размерность, переходную от 2 к 3. Потому описание этой системы аналитическими соотношениями, получен- ными коэволюционным алгоритмом генетического программирования, представляется полезным. Испытание алгоритма на тестовых примерах показывает, что при правильном выборе функционального множества алгоритм находит функцию, генерирующую выборку. Эта дает надежду получить символьное соотношение, являющееся истинным законом, описывающим реальные физические данные, имеющие сложную природу.

Таким образом, применение коэволюционного алгоритма генетического программирования позволило построить хорошие аппроксимации рефрактометрических свойств оптически прозрачных кристаллов Rb 2 MnCl 4 и NaMnCl 3 . Исходя из сравнения аппроксимирующих соотношений и модельных описаний определена величина обменного взаимодействия между магнитными ионами. Выделен вклад в рефрактометрические свойства магнетика в парафазе, обусловленный механизмами, не связанными с флуктуациями вектора антиферромагнетизма.