Применение комбинационных колебаний для повышения точности неразрушающего контроля стальных изделий

Введение. Опыт применения методов электромагнитной оценки качества упрочнения по основным гармоникам многочастотного сигнала [1] показал, что при контроле толщины упрочнённого слоя отдельных видов упрочнения поверхности стальных изделий возникает недопустимо большая погрешность. Рассмотрим причину возникновения погрешности, используя уравнения сигнала электромагнитного преобразователя с П-образным ферромагнитным сердечником [2, 3].

Влияние толщины упрочнённого слоя на сигнал датчика. Для большей наглядности будем считать свойства упрочнённого слоя неизменными по глубине. Тогда контролируемое изделие можно рассматривать как состоящее всего из двух слоёв — упрочнённого и основы (рис. 1). Магнитное сопротивление контролируемой среды зависит от толщины h упрочнённого слоя, его можно выразить [4]:

где 14 и ц₂ — комплексная магнитная проницаемость упрочнённого слоя и основного металла соответственно; Ь — длина преобразователя;

юц2ст2

где ^ и ст₂ — удельная электропроводность упрочненного слоя и основного металла соответственно; а - с— расстояние между полюсами.

Зависимость ЭДС от толщины h упрочнённого слоя определяется коэффициентом в выражении (1), определяющим отражение волны на границе раздела упрочнённого слоя и основного металла:

Ml ^-2^ _ |

1637

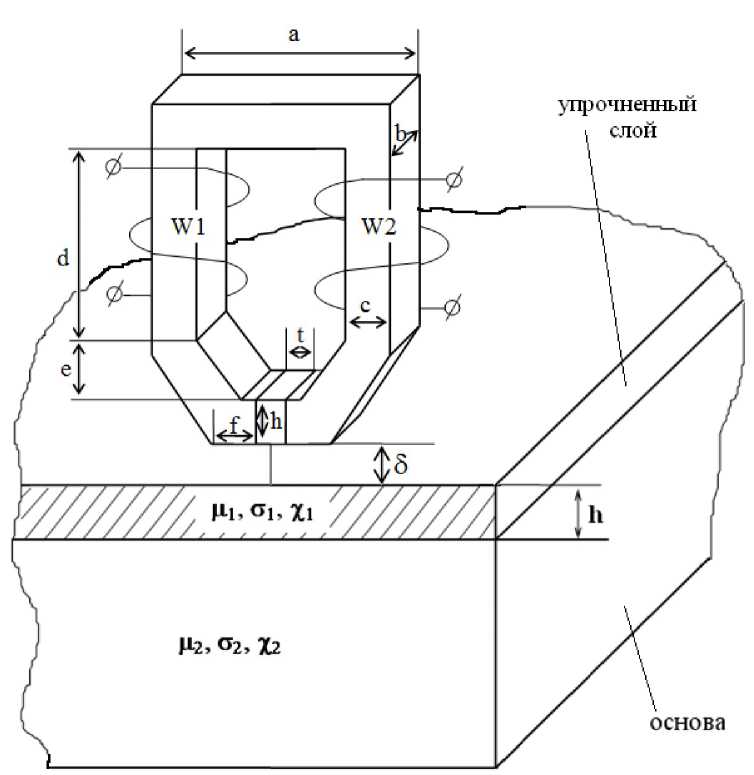
Рис. 1. Электромагнитный преобразователь, установленный над двухслойной средой

Для упрощения анализа рассмотрим только плоскую волну (к = 0), которая в выражении (1) превосходит по величине все остальные волны. Коэффициент (2) для плоской волны (при к = = 0) примет вид:

Ц2СТ1                                                                             ' ‘

При всех известных видах упрочнения, вызывающих физические дефекты в идеальном кристалле железа, магнитная проницаемость ^ и удельная электропроводность с^ упрочнённого слоя уменьшаются по сравнению с магнитной проницаемостью ц2 и удельной электропроводностью ст2 основной стали. Если упрочнение изменяет рис пропорционально, то выражение (3) стремится к нулю и преобразователь теряет чувствительность к толщине упрочнённого слоя. В действительности же при упрочнении электрические и магнитные свойства изменяются не пропорционально, поэтому выражение (3) не равно нулю, но имеет небольшую величину. Сигнал отражённой волны на границе раздела слоёв настолько мал, что его могут превосходить помехи, вызванные вариациями ц1Л ^ в упрочнённом слое и вариациями ц2, ст2 основного металла. Это и является причиной возникновения недопустимо большой ошибки при контроле некоторых видов упрочнения по основным гармоникам сигнала преобразователя.

1638

Ситуацию можно улучшить, если использовать комбинационные колебания [5, 6], которые возникают при взаимодействии гармонических волн в нелинейной среде. При подаче двух синусоидальных (основных) колебаний с различными частотами fi и £ в нелинейной среде возникают комбинационные колебания с частотами ± I ■ fi ± J ■ £, где I и J— целые числа. По сравнению с высшими гармониками комбинационные колебания обладают рядом преимуществ:

— имеют базис, ортогональный базису основных и высших гармоник, поэтому отпадает необходимость в фильтрации токов возбуждения преобразователей;

— частоту комбинационных колебаний можно регулировать, делая её значительно отличной от частоты основных и высших гармоник, что упрощает гармонический анализ сигнала преобразователя;

— амплитуда комбинационных колебаний в рэлеевской области поля значительно превосходит амплитуды высших гармоник при равных действующих значениях токов возбуждения датчика.

Рассмотрим комбинационные колебания в неблагоприятных условиях, когда на границе упрочнённого слоя нет отражения волны, выражение (3) равно нулю и основные гармоники сигнала измерительного преобразователя не зависят от толщины упрочнённого слоя h. Если две синусоидальные волны с тангенциальной напряжённостью Н магнитного поля распространяются от поверхности вглубь контролируемого металла с коэффициентами затухания о и коэффициентами фаз Р, то в упрочнённом слое эти коэффициенты будут равны:

1    7 Pi - 7 ^-10) ^_

-47®^,

а в основном металле:

^2  7Р2 — 7^20 —

Для аналитического решения поставленной

^7'соц2о2 .

задачи примем, что при близких значениях

частот го1 » ю2 коэффициенты затухания и коэффициенты фаз двух указанных волн соответственно равны между собой. Тогда волновые уравнения в упрочнённом слое примут вид:

Н_х = H_me”°^vX sin (ю^ + у - р^),

Н2 = Н,,,е"х sin(co2f + т - IV), где Нт — амплитуда напряжённости магнитного поля на поверхности упрочнённого слоя. Волны преломляются в основной металл без отражения и описываются уравнениями

Н_х = H_me^_aihe^^x-h^ sin^co/ + ф -р^ - р₂ (% - Л)] Н₂ = н_me^-C4he^^x-h'⁾ sin [co₂f + у - р^ - р₂ (х - Л)]

В работе [5] аналитически доказано, что в нелинейной среде с коэффициентом Рэлея % в результате взаимодействия двух волн напряжённости будут образовываться комбинационные волны индукции магнитного поля. Так, в упрочнённом слое суммарная комбинационная волна индукции третьего порядка представлена зависимостью:

5 = _6Xi^.e-2a1xsinr/ +2Ю2)г+3^-3^%!.(6)

л              LJ

В основном металле комбинационная волна индукции третьего порядка равна:

В = _^Ig-z^Ag^tx-A) sin[^ + 2co2)f + з^ - 3^/7 - Зр2 (% - Л)](7)

Из выражений (6) и (7) можно найти комплексные амплитуды индукции в упрочнённом слое и основном металле:

В_т1 = -^у²²-expy 3\у exp (-204 -узр^х, л

6v Н²

В_т2 =- ₂^mexp[(a₂ -а₁)2/? + 73(47-3^+ Р₂Л)]exp(-2а₂ - j3p₂)x.

В соответствии с (8) комплексное значение амплитуды магнитного потока: = biB_mdx = b^B_mYdx +

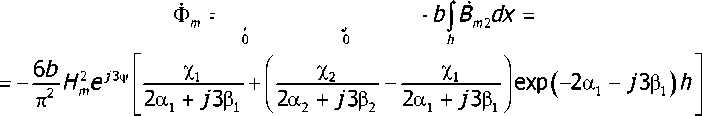
Этот поток сцеплен с измерительной обмоткой датчика 144 и, изменяясь с частотой ю₁ +2ю₂, наводит в ней ЭДС сигнала комбинационных колебаний:

у2л

Xi ! Х₂ 2ос₁ + j'3p_i ^2а₂ + j3p₂

-—/лехр(-2а. -Зур,)Л 2ai+j3pJ v 1     17

После упрочнения стали резко изменяется коэффициент Рэлея ^ «:у2, поэтому сигнал комбинационных колебаний (9) даже в отсутствие явления отражения волны на границе двух сред однозначно зависит от толщины упрочнённого слоя.

Таким образом, можно ввести критерий, позволяющий оценить чувствительность сигнала датчика к толщине упрочнённого слоя для основных и комбинационных колебаний и тем самым определить применимость комбинационных колебаний для контроля толщины упрочнённого слоя. Критерий применимости комбинационных колебаний. Влияние толщины слоя на основные колебания показывает коэффициент отражения (3), который мы будем считать коэффициентом чувствительности по основным колебаниям:

(Ю)

(И)

''осн л .             "

У Ц2СТ1

Коэффициент чувствительности по комбинационным колебаниям определяем по выражению:

Х2

Х1

_ 2а₂ + j3p₂ 2a_t + j'3p₁ ^А комбинац ^—

Xi

2^ + j'3pi

Тогда можно ввести критерий применимости комбинационных колебаний для контроля толщины упрочнённого слоя:

pj _ комбинац

Например, слой на поверхности стали 40Х, прошедшей борирование, закалку и низкий отпуск, имеет следующие параметры:

щ =42-4л-10 7 Гн/м, о. = 3-106 См/м, %. = 1,7 -10 2 Гн/А.

Основной металл имеет отличные, в особенности по коэффициенту Рэлея, параметры:

= 75-4л-10 7 Гн/м, ст, = б-106 См/м, у, =4,7-10 2 Гн/А.

В этом случае величина коэффициента (10) мала:

к = №.-1 = 0,058, ^осн

1640

что практически не позволяет контролировать толщину упрочнённого слоя по основным гармоникам. Коэффициент

Х2

Х1

К =

Акомбинац

2oc₂+j3p₂ 2а₁+уЗр₁ __{0 44}

Xi                    '

2^ + j3pi достаточно велик, и, соответственно, у-у _ комбинац = 7,58.

Косн

Таким образом, комбинационные колебания будут приблизительно в 7 раз эффективнее основных для практического контроля толщины боридного слоя.

Зависимость информативности комбинационных колебаний в сигнале электромагнитного преобразователя по сравнению с основными колебаниями при различных помехах (например, вариации зазора между измерительным преобразователем и контролируемой поверхностью) удалось исследовать благодаря использованию имитационной модели, включающей математическую модель образования сигнала электромагнитного преобразователя, расположенного над нелинейной ферромагнитной проводящей средой с изменяющимися по толщине свойствами [7].

Применение комбинационных колебаний для повышения точности неразрушающего контроля. Сигнал электромагнитного преобразователя зависит от геометрических факторов, толщины упрочнённого слоя /?, зазора между датчиком и контролируемой поверхностью. Кроме того, сигнал зависит от электромагнитных свойств упрочнённого слоя и основного металла. Электромагнитные свойства определяются структурным состоянием стали и используются для струк-туроскопии. Роль этих факторов зависит от задачи контроля: например, если контролируется толщина упрочнённого слоя, то все остальные факторы являются мешающими. Влияние каждого фактора удобно представлять нормированным передаточным коэффициентом этого фактора, например, передаточный коэффициент толщины упрочнённого слоя h\

* f ah где hH — номинальная толщина упрочнённого слоя, f— частота, Е (Г) — частотная характеристика ЭДС датчика.

Отношение полезного сигнала к помехе оценивается отношением передаточного коэффициента контролируемого фактора к передаточному коэффициенту мешающего фактора, например: a_h/a_p.

При контроле электромагнитным преобразователем толщины упрочнённого слоя h вариации зазора б являются мешающими факторами. Нормированный передаточный коэффициент зазора между датчиком и контролируемой поверхностью вычисляется следующим образом:

а А аЁ^

5 f 88

где бн — номинальный зазор между торцом преобразователя и контролируемой поверхностью;

Е— ЭДС гармоник; f— частота сигнала.

Отношение сигнала к помехе можно отразить отношением передаточного коэффициента контролируемого фактора h к передаточному коэффициенту мешающего фактора б.

На рис. 2 показаны частотные характеристики отношения модулей передаточных коэффициентов толщины упрочнённого слоя и зазора a_h / а₅.

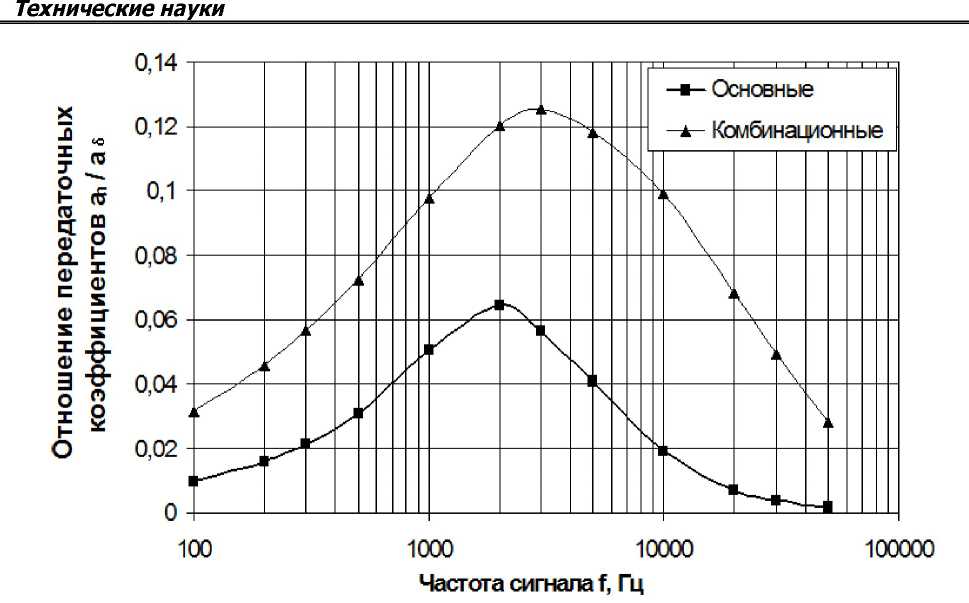
Рис. 2. Частотные характеристики отношения модулей передаточных коэффициентов толщины упрочнённого слоя и зазора

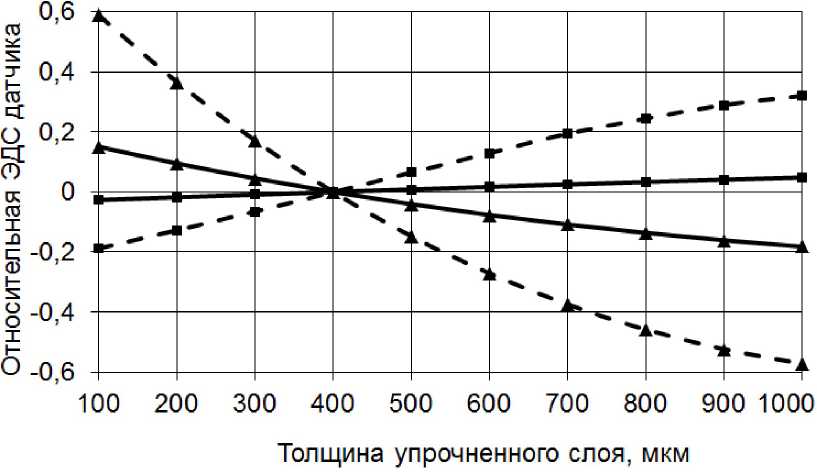
—■—Основные -■-Комбинационные

Рис. 3. Зависимость относительной ЭДС датчика от толщины упрочнённого слоя для основных и комбинационных колебаний

На всех частотах отношение сигнала к помехе в комбинационных колебаниях значительно выше, чем в основных гармониках. Исследования на имитационной модели подтверждают, что относительное влияние зазора в комбинационных колебаниях меньше, чем в основных гармониках сигнала датчика, в частности, использование комбинационных колебаний даёт меньшую погрешность контроля по сравнению с основными гармониками при значительных вариациях зазора.

1642

Для выяснения причин, по которым отношение полезного сигнала к помехе в комбинационных колебаниях выше, чем в основных, проведено исследование сигнала дифференциально включённых электромагнитных датчиков. На рис. 3 показана зависимость относительной ЭДС датчика для основных и комбинационных колебаний от толщины упрочнённого слоя. Из приведённых графиков видно, что изменения толщины упрочнённого слоя (полезного сигнала) вызывают гораздо большее изменение ЭДС комбинационных колебаний по сравнению с ЭДС, вызванной основными колебаниями.

Сигнал суммарного комбинационного колебания третьего порядка почти в девять раз больше изменяется по сравнению с сигналом основных гармоник при изменении толщины упрочнённого слоя в пределах от 100 до 1000 мкм.

Влияние толщины упрочнённого слоя на основные гармоники обусловлено двумя процессами: отражением основных волн на границе между упрочнённым слоем и основным металлом и затуханием волны в упрочнённом слое. В результате упрочнения в стали образуется слой с такими электромагнитными свойствами, которые дают слабое отражение на границе раздела слоёв. Поэтому влияние толщины упрочнённого слоя в основных гармониках слабое.

Комбинационные колебания возникают в магнитно-мягкой части основного металла даже в отсутствие отражения, и их сигнал однозначно связан с толщиной упрочнённого слоя из-за за-

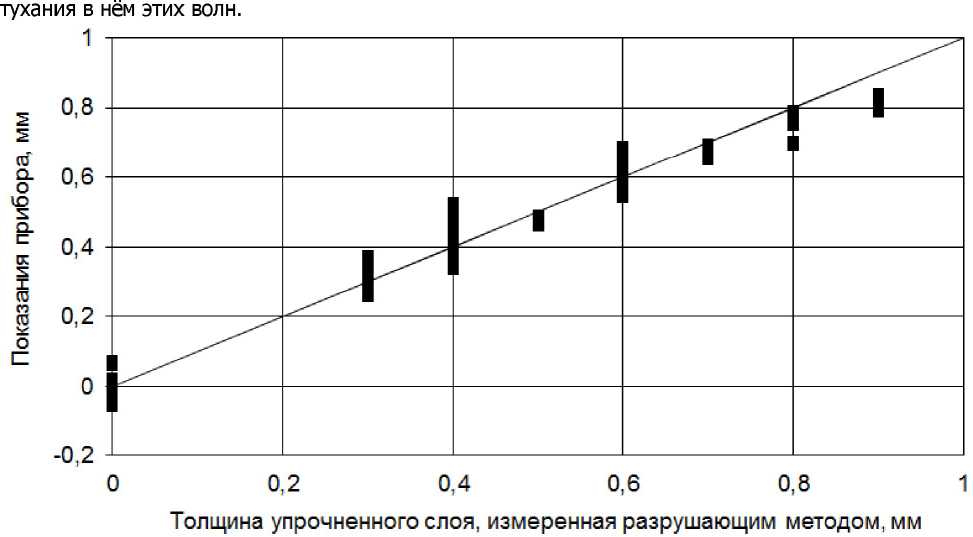
Рис. 4. Сравнение результатов измерения толщины упрочнённого слоя, полученных разрушающим способом с показаниями прибора, использующего комбинационные колебания

Несмотря на то, что комбинационные колебания сильнее основных подвержены мешающему влиянию зазора между датчиком и контролируемым изделием, они подвержены ещё большему влиянию по сравнению с основными колебаниями со стороны контролируемого фактора — толщины упрочнённого слоя. Поэтому отношение полезного сигнала к помехе в них выше, чем в основных гармониках. Использование комбинационных колебаний как компонента многомерного сигнала повышает точность неразрушающего контроля толщины упрочнённого слоя.

Преимущества использования комбинационных колебаний были доказаны экспериментально.

Экспериментальная оценка повышения точности неразрушающего контроля при использовании комбинационных колебаний. Опытный прибор настраивался и испытывался на кольцах карданных подшипников, упрочнённых цементацией, любезно предоставленных нам центральной заводской лабораторией ГПЗ-10. Это были не специально изготовленные образцовые изделия, а серийные кольца, прошедшие разрушающие испытания при периодической проверке технологического процесса цементации. Кольца выбирались с различной глубиной цементации в течение достаточно большого отрезка времени.

На рис. 4 и 5 показаны регрессионные зависимости показаний прибора при измерении толщины упрочнения. Среднеквадратическое отклонение показаний прибора от данных разрушающих испытаний составило 7,4 % от диапазона исследуемых толщин (от 0 до 1 мм). Среднеквадратическая погрешность без использования комбинационных колебаний составила 20,5 %.

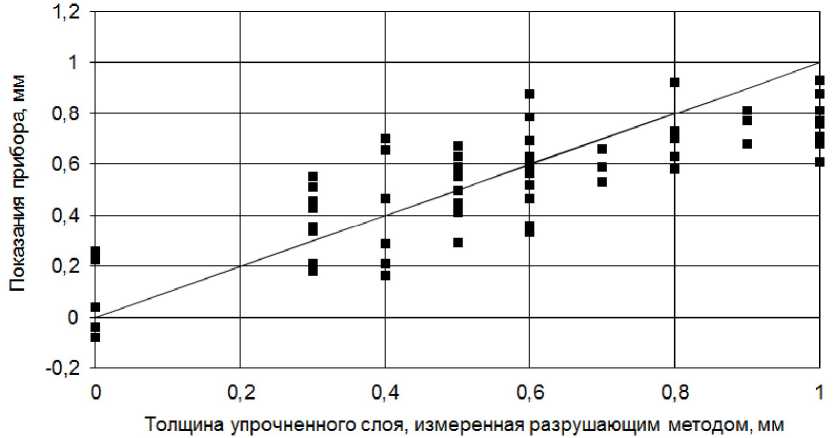
Рис. 5. Сравнение результатов измерения толщины упрочнённого слоя, полученных разрушающим способом с показаниями прибора, использующего основные колебания

Выводы. Несмотря на то, что в сигнале датчика амплитуда комбинационных колебаний намного ниже, чем основных, и их выделение представляет довольно сложную техническую задачу, применение комбинационных колебаний позволяет значительно повысить точность контроля толщины упрочнённого слоя стальных изделий.