Применение комплексного метода бокса для решения задач оптимизации параметров ходовой части транспортных машин

используют либо модифицированные с учетом ограничений методы безусловной оптимизации, либо преобразуют задачу с ограничениями в задачу без ограничений (так называемая последовательная оптимизация без ограничений или метод штрафных функций) [1, 3].

Для задач безусловной оптимизации разработаны эффективные, надежные и теоретически обоснованные методы. Методы безусловной оптимизации, используемые на отдельных этапах работы алгоритмов нелинейной оптимизации, можно разделить на две крупные группы:

• -    методы, использующие только значения функций или прямые методы, например, метод поиска по образцу (метод Хука-Дживса) и метод деформированного многогранника (метод Нелдера-Мида);

• -    методы, использующие производные или градиентные методы, например, метод наискорейшего спуска, метод сопряженных градиентов (Флетчера-Ривса) и метод сопряженных направлений (Дэвидона-Флетчера-Пауэлла).

Градиентные методы позволяют ускорить сходимость оптимального процесса. Однако, чаще всего, в задачах оптимального проектирования параметров элементов ходовой части функция цели находится в результате анализа некоторого динамического процесса на определенном промежутке времени. Моделирование и исследование таких процессов проводят с использованием численных методов. Это значительно затрудняет получение производных целевой функции и функций ограничений. В работе Г. Реклейтиса, А. Рейвиндрана, К. Рег-сдела [1] предложено использовать численные аппроксимации градиентов, что так же увеличивает число вычислений функции цели. Поэтому в задачах большой размерности практически такой подход не нашел применения.

Один из наиболее перспективных методов решения задачи оптимального проектирования упругих конструкций разработан Э. Хогом - ме- тод чувствительности [2]. Суть данного алгоритма заключается в нахождении векторов чувствительности, определяющих зависимость целевой функции от переменных проектирования. Анализ чувствительности позволяет получить значения градиентов, которые требуются для всех градиентных методов оптимизации проекта.

Чтобы сравнить эффективность различных методов была выбрана задача минимизации функции Розенброка ( f(x)=100*(x₂-x₁²)²+(1-x₁)² ) (рис. 1).

Результаты проведенных тестовых расчетов показывают, что метод Дэвидона-Флетчера-Па-уэлла (ДФП) является наиболее эффективный из градиентных. Метод прямого поиска - комплексный метод Бокса (модифицированный с учетом ограничений метод деформированного многогранника (метод Нелдера-Мида) [3] -практически сопоставим с методом Флетчера-Ривса и методом наискорейшего спуска (рис. 2).

Особенностью исследования динамики ходовых систем транспортных машин является то, что они включают в себя большое количество элементов, имеющих между собой как вязкоупругие, так и кинематические связи (голоном-ные и неголономные). Динамическое поведение таких объектов описывается многомерной системой, включающей дифференциальные и алгебраические уравнения. Значение целевых функций получаются в результате решения системы уравнений на каждом шаге оптимизационного процесса.

В настоящей работе предлагается использовать метод временных конечных элементов [6, 7], который позволяет непосредственно учитывать кинематические связи. Основные соотношения и реализация метода в применении к анализу динамических систем изложены в [8]. Метод конечных элементов адаптируется для решения задач динамики, описанных системой дифференциально-алгебраических уравнений, т.е. с учетом кинематических связей.

На основе комплексного метода Бокса, использующего для поиска функции цели алгоритм метода временных конечных элементов разработан программный комплекс для расчета оптимальных параметров ходовых систем колесных и гусеничных транспортных машин [10].

Работоспособность предлагаемых алгоритмов была проверена при проведении оптимизационного расчета параметров подвески транспортного средства, представляющего четырехмассовую модель с пятью степенями свободы (рис. 3) [6,7].

Оптимизационный расчет параметров подвески машины проводился с целью снижения максимальной амплитуды ускорений на водительском месте Z»_max1 . В настоящей работе алгоритм оптимального проектирования на основе комплексного метода Бокса сравнивается с методом проекции градиента. В результате проведенного расчета и сравнения разных методов получены следующие данные: оптимизационный расчет с использованием метода

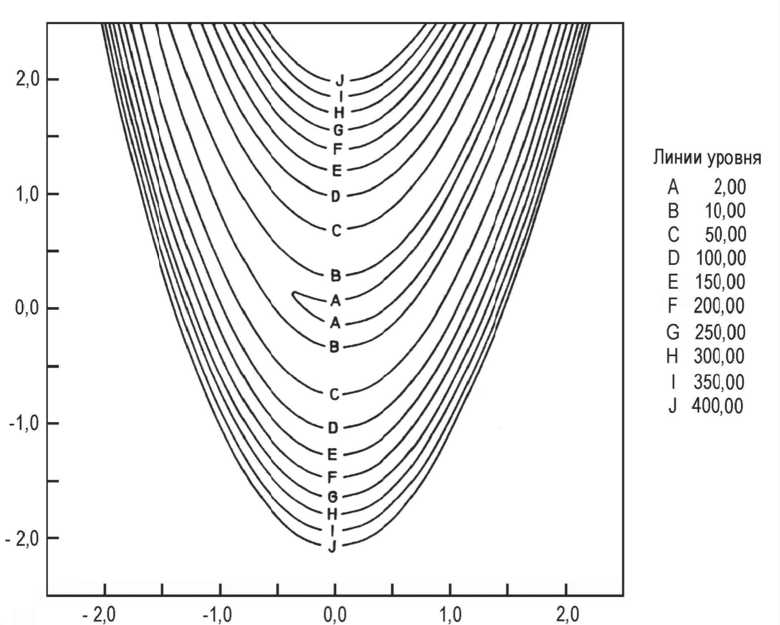
Рис. 1. Функция Розенброка

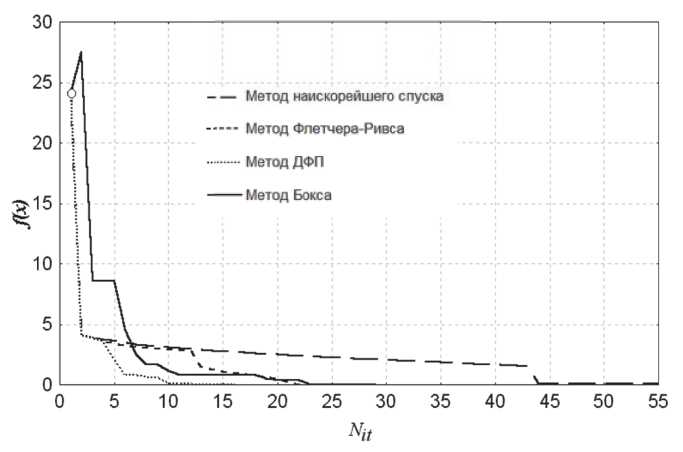
Рис. 2. Графики оптимизационных процессов

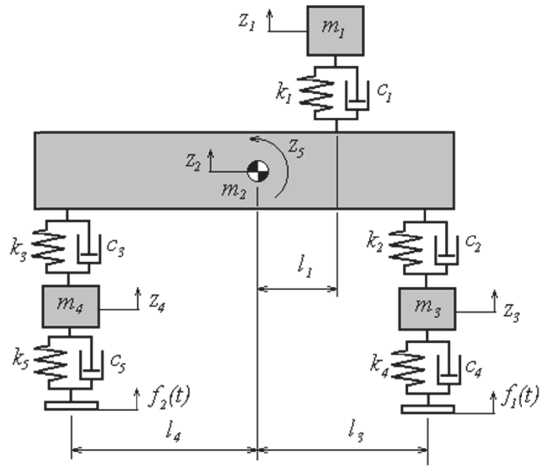
Рис. 3 . Четырехмассовая механическая система

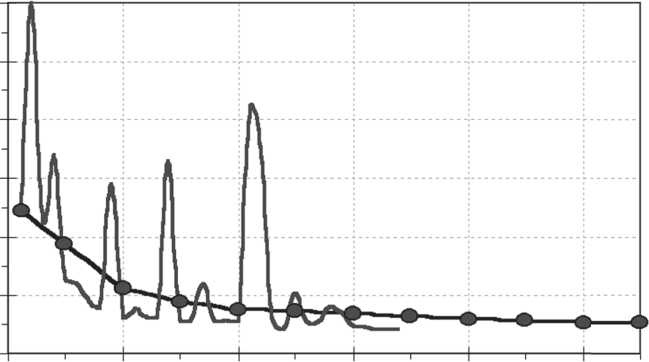
Бокса привел к уменьшению значения функции цели c 8,42 м/с2 до 6,453 м/с2 (метод проекции градиента – 6,538 м/с2) (рис. 4). Предлагаемый алгоритм проведения оптимизационных расчетов сложных механических систем с упругими и вязкоупругими связями показал хорошую сходимость и экономичность. Это позволяет считать возможным использование прямого метода Бокса с расчетом функции цели методом временных конечных элементов для решения задач оптимизации конструкции ходовых систем транспортных машин.

Предложенный алгоритм был использован для решения оптимизационных задач снижения динамической нагруженности элементов ходовой части быстроходной гусеничной машины (ГМ) с торсионной подвеской. Постановка задачи оптимизации имеет следующую фор- мулировку: выбрать рациональные параметры упругих и демпфирующих элементов подвески машины с целью минимизации максимальных амплитуд динамических нагрузок, действующих на детали подвески.

Для описания состояния динамической системы вводятся следующие обобщенные координаты (рис. 5) в глобальной системе координат XYZ: вертикальная координата центра масс гусеничной машины, углы поворота корпуса относительно продольной и поперечной осей q=[z, j _x , j_y]^T .

Ходовая часть включает N_k катков, имеющих индивидуальное подрессоривание. Связь между каждым i катком и корпусом моделируется в виде пружины с приведенным коэффициентом жесткости К_i и коэффициентом демпфирования C_i . Положение каждого катка описывается координатами х_i и y_i относительно центра масс корпуса.

1 2,0

1 1 ,0

1 0,0

у

9 ’°

N

8,0

7,0

6,0

0            1 0           2 0           3 0           4 0           5 0     11

—Q—Метод проекции градиента

---Комплексный метод Бокса

Рис. 4. Графики оптимизационных процессов

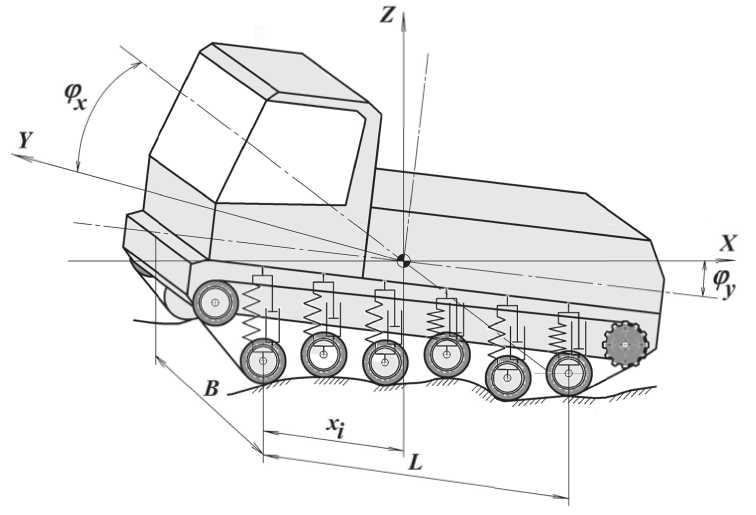
Рис. 5. Расчетная модель гусеничной машины

В таблице 1 приводятся исходные данные для проведения расчетов. Основные вопросы моделирования динамического поведения гусеничной машины и расчетные данные приведены в работе [9].

Нагруженность элементов подвески характеризуется динамическим сжимающим усилием Р д и крутящим моментом М д , действующим на торсион со стороны опорного катка. Анализ расчетов при различных дорожных условиях выявил следующее: наиболее нагруженными являются элементы подвески передних катков. Была выявлена зависимость максимальных амплитуд динамической нагрузки от изменения приведенных коэффициента жесткости торсиона и коэффициента демпфирования амортизатора (рис.6).

Проведенный оптимизационный расчет позволил снизить динамическую нагруженность элементов подвески на 10,14% (с 33,6 кН до 30,2 кН). В таблице 2 приводятся значения варьируемых параметров для исходной и оптимальной конструкции подвески катков.

Результаты работы позволяют сделать следующие выводы:

• -    предложенный алгоритм оптимизации на основе прямого метода Бокса показал хорошую сходимость экономичность;

• -    использование разработанного на основе предложенного метода программного комплекса расчета оптимальных параметров элементов подвески гусеничной машины позволило снизить динамическую нагруженность деталей.

Таблица 1. Исходные данные

№	Наименование параметра	Обозначение	Значение
1	Масса ГМ с полной нагрузкой	т , кг	17960
2	Максимальная скорость движения	v , км/ч	52,4
3	Длина опорной ветви гусеницы	L , м	4000
4	Момент инерции корпуса ГМ относительно продольной оси	Jx , кг - м2	45500
5	Момент инерции корпуса ГМ относительно поперечной оси	Jy , кг - м2	78000
6	Приведенный коэффициент жесткости упругого элемента	K , кН - с/м	195
7	Коэффициент демпфирования амортизатора	C , кН-с/м	4

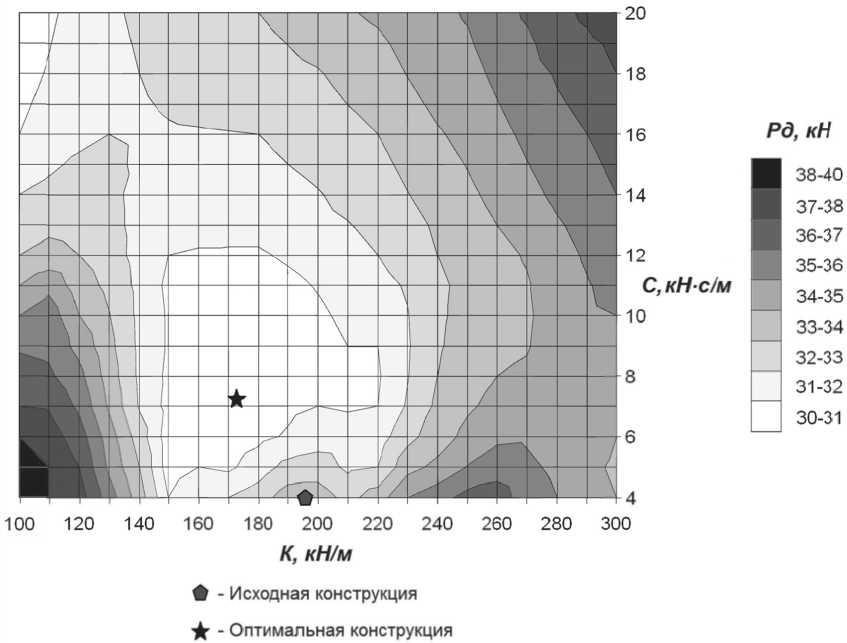
Рис. 6. Зависимость динамической нагруженности элементов подвески первого катка от коэффициентов жесткости K и демпфирования C

Таблица 2. Значения варьируемых параметров для исходной и оптимальной конструкции подвески катков

Параметр	Исходное значение	Нижнее ограничение	Верхнее ограничение	Оптимальное значение
Коэффициент жесткости К, Н/м	195	100	300	173
Коэффициенты демпфирования С, Н ■ с/м	4	4	20	7,25