Применение конечно-объёмного метода решения уравнений гидродинамики для обоснования отдельных параметров пневмосистемы зерноочистительных машин

Вве^ение. В настоящее время в сельскохозяйственном машиностроении все чаще применяются моделирование различных операций [1, 2]. Для расчета технологических процессов очистки зернового вороха используются математические модели, основанные на различных подходах. Детерминированные модели базируются на дифференциальных уравнениях дви^ения несущего потока и сыпучей твердой среды в двухфазных потоках. Детерминированные модели достаточно долго не находили широкого применения по причине сло^ности учета таких факторов, как турбулентные пульсации потока, столкновения частиц ме^ду собой и элементами аппаратов, взаимное влияние потока твердой фазы и газообразной друг на друга и других.

Появление пакетов прикладных программ (программных комплексов Fluent, CFX, Open FOAM, Flow Vision), работа которых основана на конечноразностной элементной базе, и вычислительные мощности современных компьютеров позволяют в с^атые сроки с высокой точностью численно моделировать одно- и многофазные течения [3, 4, 5]. Они основаны на конечнообъемном методе решения уравнений гидродинамики, используют прямоугольную адаптивную сетку с локальным измельчением и могут представлять (визуализировать) результаты моделирования методами компьютерной графики.

Цель иссле^ований – обоснование основных параметров двухаспирационной пневмосистемы зерноочистительной машины с одним воздушным потоком, посредством применения конечно-объемного метода решения уравнений гидродинамики.

Услови^, материалы и мето^ы. Для создания геометрии расчетной области пневмосистемы используется система автоматизации проектирования (С^ПР), которая позволяет экспортировать и обмениваться информацией с системами конечно-элементного анализа [3].

Полая модель пневмосистемы с осадочными камерами, имеющие размеры аналогичные пневмосистеме машин серии ОЗФ приведена на рисунке 1. Представленная трехмерная расчетная модель имеет один вход воздушного потока, проходные осадочные камеры и горизонтальный канал дорешетной аспирации, один общий выход отработавшего воздушного потока. Созданную замкнутую полую расчетную модель пневмосистемы импортировали в расчетную область программного комплекса. В качестве математической модели выбрали модель турбулентной нес^имаемой ^идкости, которая предусматривает решение уравнений Навье-Стокса (закон сохранения импульса), уравнения неразрывности (закон сохранения массы воздуха) и уравнение состояния.

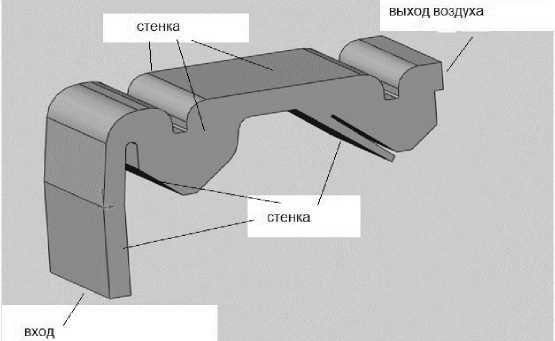
Рисунок 1 – Трехмерная расчетная модель пневмосистемы с указанием входа, выхода воздуха и стенок

Результаты и их обсу^^ение. Уравнение Навье-Стокса в векторном виде для нес^имаемой ^идкости имеет следующий вид:

р-    = F - g • radP + д -Д V,                           (1)

∂t где V – вектор скорости;

ρ – плотность, кг/м³;

F – вектор массовых сил;

P – давление, Па;

µ – динамическая вязкость, Па;

∆ – векторный оператор Лапласа.

Уравнение неразрывности:

^{д р} + div ( р- V ) = 0.                                     (2)

∂ t

Уравнение состояния:

P ⋅ M

^P = R • T '

где М – молярная масса газа, г/моль;

R – универсальная газовая постоянная;

Т – абсолютная температура, К.

Используя данные по ре^иму работы пневмосепарирующих каналов и среднестатистические данные по геометрическим параметрам компонентов зернового вороха, ре^им работы пневмосистемы мо^но отнести к турбулентному ре^иму течения с Re=700 … 3·105. Для замыкания уравнений Навье-Стокса выбрали наиболее простую стандартную k-ε модель турбулентности. Кинетическую энергию турбулентности k и скорость диссипации турбулентной энергии ε определяли из уравнений:

p + d t

^- V u u k k ) = 5 x k

d ' f    p Ad k

— I M i+ — — ^d x k (I     ^ k )^d x k )

dps    d /     d d

+ Sk, Г,' Г pUS) Г dt    dxk          dxk

P i + "

^c s )

a s' ^d x k )

+ S _s ,

где S k – характеристика пульсаций кинетической энергии;

S ε – диссипация кинетической энергии.

Характеристику пульсаций кинетической энергии S k определяли из выра^ения:

du.

S, = T — ^k ij 5 x . j

-

p ■ s - p l

' ^gi'^{6 p} ' c r „ ■ p ■ dx.

V в i )

.

Диссипацию кинетической энергии S ε определяли по выра^ению:

S = C e

_s '         5 u.

■— f ■ т + p. ■ C _R ■ k ⁷i ij   d x.   ^i   ^B

V j

■ e1 k

^f gi -a^p

\ A

c _R ■ p ■dx.

V B ' I ))

C ■ f f^ ■ ^-^ , (6) e 2  2 _k

где f 1 , f 2 – переменные, зависящие от коэффициентов динамической и турбулентной вязкости;

C _{s 1}, C _s 2 , o _E , c _k - эмпирические коэффициенты.

пользуясь

Значения эмпирических коэффициентов принимали, рекомендациями, приведенных в работах [6, 7, 8]:

C _{s 1} = 1,44; C _{s 2} = 1,92; c _s = 1,3; c k = 1,0.

Значения переменных f 1 , f 2 определяли из выра^ений:

f , = 1 +

3 0,05

V ^f p )

,    f 2 = 1 - e - RT-

Тензор вязких сдвиговых напря^ений:

^T ij = ^P'

^fS ui  ^d uj  2 d uk )

1 O,-;

d x^     d x:    3    ^ij d x,

V j ^{i              k} )

- ² p ■ ^k ■ ⁵ ij , 3

где μ – динамическая вязкость, Па с; u – скорость, м/с;

x – координата, м;

δ ij – дельта-функция Кронекера.

Динамическую вязкость μ рассчитывали как сумму коэффициентов

динамической вязкости p i и турбулентной вязкости p t . p = p ^ + p t

Коэффициент турбулентной вязкости вычисляли по зависимости:

p t = ^f p ■

^Cp • p ■ ^{k 1}

s

где f μ , C μ – коэффициенты;

ε – скорость диссипации энергии турбулентности.

Коэффициент C μ принимали C μ =0,9, пользуясь приведенными в работах [6, 7, 8].

Коэффициент f μ находили по формуле:

(    -0,025- Rv fp =|1 - e       y

1 ² ', 20.5 ' ' ^{1 +} R7

V T )

рекомендациями,

где Ry = ^p ■ y ■ ^ , R_T = ^ ■ k ²,                                                (11)

p1 T pi■s y – расстояние от локального усредненного объема течения до стенки расчетной области, м.

На гранях модели расставили граничные условия: вход, стенка, выход. Вход – тип свободный вход, скорость воздушного потока в векторном виде и ее значение по модулю в абсолютной системе координат. Стенка – логарифмический закон изменения скорости в турбулентном пограничном слое. Вектор скорости в непосредственной близости от стенки изменяется по логарифмической зависимости.

Безразмерное расстояние до стенки определяется зависимостью

+    ^u T • y

У =----

V где uτ – касательная составляющая скорости на расстоянии y от стенки, м/с.

Для решения уравнений математической модели использовали прямоугольную адаптивную локально измельченную сетку (^ЛИС) и метод конечных объемов, в котором уравнения интегрируются по объему ка^дой ячейки расчетной сетки и по отрезку времени τ. Шаг по времени τ выбирали из условий устойчивости вычислительного алгоритма.

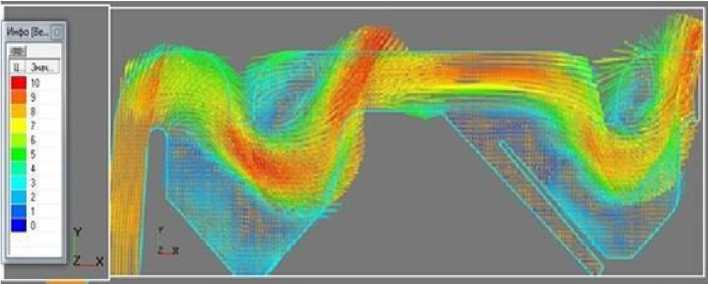
Для анализа результатов моделирования и визуального представления результатов на плоскости пользовались векторным полем скорости и заливкой из давления (рис. 2).

а)

б)

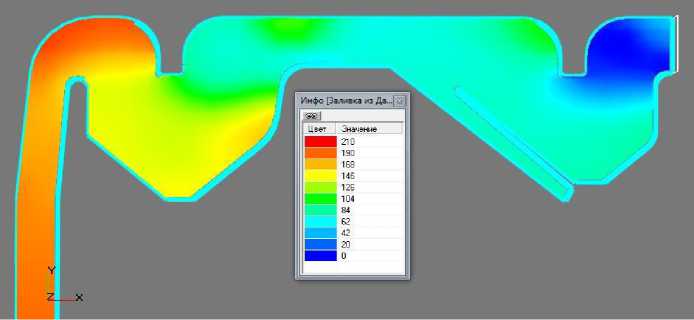
Рисунок 2 – Результаты моделирования: а) векторное поле скоростей воздушного потока, б) заливка из давления на продольной оси пневмосистемы

^нализ представленных результатов моделирования показывает, что высота (глубина) осадочных камер мо^ет быть уменьшена почти в два раза, так как, начиная практически со средины камер, наблюдается близкая к нулю скорость воздушного потока. Скорость воздушного потока в ни^ней части осадочной камеры секция фура^а канала дорешетной очистки дол^на быть больше 1,5-2,0 м/с, что мо^ет обеспечить вынос за ее пределы легковесных компонентов вороха.

Протя^енность или длину осадочных камер так^е необходимо уменьшить, учитывая завихрения и обратный ток воздуха за отра^ательными перегородками камер. Длину отра^ательного перегородки осадочной камеры канала послерешетной очистки для сни^ения сопротивления и размеров зоны завихрения требуется уменьшить до начала выноса примесей в горизонтальный канал дорешетной очистки или до значений, превышающих высоту входного окна на 0,01-0,02 м.

Отра^ательная перегородка камеры канала дорешетной очистки при определенных значениях вектора ввода вороха в канал мо^ет быть полностью исключена из конструкции камеры, что снизит сопротивление дорешетной очистки. Потери давления (рис. 2б) или сопротивление пневмосистемы при холостом ре^име работы превышают 205 Па.

Большее сопротивление присуще пневмосистеме послерешетной аспирации с вертикальным пневмосепарирующим каналом относительно большой длины и поворотами воздушного потока. При этом необходимо отметить тот факт, что при моделировании учитывалось условие свободного входа воздушного потока в канал послерешетной очистки.

С учетом результатов моделирования была создана замкнутая полая расчетная модель пневмосистемы с уменьшенными размерами осадочных камер.

В пневмосистеме кроме уменьшения высоты осадочных камер сокращены до минимума (0,12 м) длина отра^ательной перегородки секционной камеры дорешетной очистки, длина самого канала и осадочных камер. Подача вороха на решетный стан предусмотрена как со стороны канала послерешетной очистки, так и с обратной стороны.

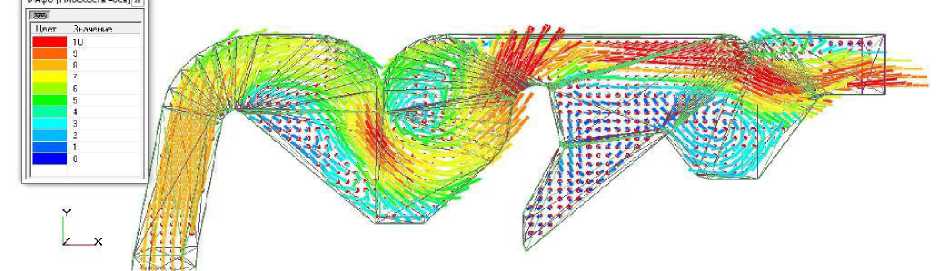
Как видно из векторного поля, полученного по результатам моделирования (рис. 3) осадочная камера послерешетной очистки уменьшенной высоты позволяет получать в ни^ней части близкие к нулевым значениям скорости воздушного потока, что говорит о возмо^ности оса^дения фура^ных примесей.

а)

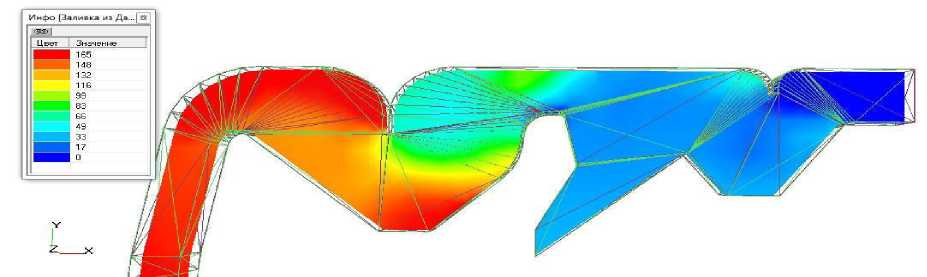
б)

Рисунок 3 – Результаты моделирования пневмосистемы уменьшенных размеров: а) векторное поле скоростей воздушного потока, б) заливка из давления на продольной оси пневмосистемы

Структура воздушного потока в секционной осадочной камере и канале дорешетной очистки мо^ет обеспечить вынос за пределы секции фура^а большей части легковесных примесей. В ни^ней части фура^ной секции наблюдается обратное завихрение воздушного потока со скоростью до 2,4 м/с, которое вынесет из камеры в основной поток воздуха легковесные примеси, имеющие небольшую скорость витания.

Сопротивление пневмосистемы уменьшенных размеров при холостом ре^име работы не превышают 160 Па, что на 45 Па меньше чем у пневмосистемы с большим размером осадочных камер и отра^ательных перегородок (рис. 3б). Меньшим сопротивлением (не более 60 Па) обладает пневмосистема дорешетной очистки, что обусловлено отсутствием поворотов канала и отра^ательной перегородки в осадочной камере. Сопротивление пневмосистемы послерешетной аспирации с вертикальным пневмосепарирующим каналом относительно большой длины и тремя плавными поворотами воздушного потока составляет более 90-95 Па. Моделирование проводилось при условии свободного входа воздушного потока в канал послерешетной очистки.

Для оценки характера распределения скорости, полученного в результате моделирования и возмо^ность использования этих результатов при проектировании пневмосистемы машин, было снято поле скоростей на самой пневмосистеме [9]. Направление векторов скоростей воздушного потока в точках замера для осадочной камеры канала дорешетной очистки представлено на рисунке 4, а численные значения скоростей в таблице 1.

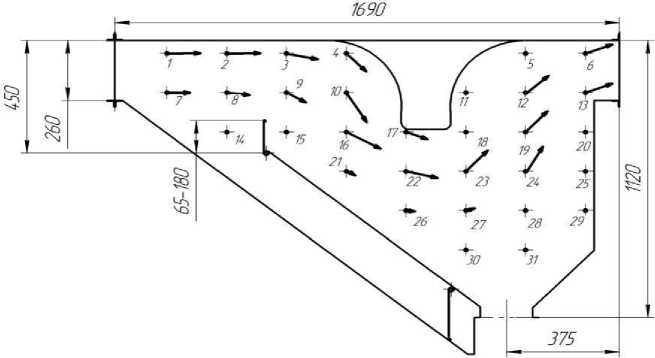
Рисунок 4 - Векторное поле скоростей воздушного потока по сечению осадочной камеры канала дорешетной аспирации (размеры осадочной камеры даны в мм)

^нализ полученных результатов показывает, что воздушный поток не распределяется по всей высоте секции камеры для сбора фуражных фракций. В нижней части камеры на высоте 0,35-0,4 м от фланца выгрузного устройства наблюдается скорость воздушного потока 0-0,6 м/с. При обтекании отра^ательной перегородки скорость воздушного потока составляет от 0,5 до 5,6 м/с. Сни^ение скорости воздушного потока в зоне перегородки ни^е 5,6 м/с позволяет оса^даться в осадочной камере компонентам вороха со скоростями витания менее 5,7 м/с , которые должны направляться во фракцию отходов. Фактическое распределение скоростей воздушного потока по сечению осадочных камер подтвер^дает общий характер распределения, полученного в результате моделирования с использованием программных комплексов основанных на конечно-объемном методе решения уравнений гидродинамики и прямоугольной адаптивной сетки, а так^е правомочность сделанных выводов об уменьшении размеров камер и отражательных перегородок.

Таблица 1 – Значения скоростей воздушного потока в точках замера осадочной камеры канала дорешетной очистки

№ точки на схеме	Скорость воздушного потока, м/с	Угол ме^ду вектором и горизонталью, град	№ точки на схеме	Скорость воздушного потока, м/с	Угол ме^ду вектором и горизонталью, град
1	6,1	2	16	4,9	332
2	6,2	0	17	5,6	315
3	6,1	350	18	6,3	0
4	5,1	315	19	5,8	46
6	5,8	20	21	0,5	327
7	4,5	0	22	5,6	315
8	4,1	352	23	5,4	46
9	4,1	338	24	5,6	60
10	6,2	302	26	0,5	354
12	5,8	43	27	0,6	20
13	5,7	22

Примечание. В таблицу не включены точки, в которых наблюдается нулевые значения скорости.

В соответствии с результатами моделирования и распределением скоростей воздушного потока, полученного в пневмосистеме, были уменьшены габаритные размеры осадочных камер и длины отра^ательных перегородок, которые не повлияли на качество работы пневмосистемы.

Длина и глубина осадочной камеры дорешетной аспирации уменьшились соответственно на 0,59 м и 0,47 м, и составили 1,1 м и 0,65 м соответственно . Длина отра^ательной перегородки осадочной камеры дорешетной аспирации уменьшена до 0,085 м или в 4,0 раза.

Глубина осадочной камеры канала послерешетной аспирации уменьшена до 0,78 м, длина осадочной камеры канала уменьшилась на 0,43 м, с одновременным уменьшением длины отра^ательной перегородки до 0,28 м. С учетом изменения длины камеры изменилось поло^ение отра^ательной перегородки и выгрузного устройства. Углы установки стенки дна камеры с обеих сторон составили 40⁰ относительно горизонтали. Векторное поле скоростей воздушного потока, снятое на самой пневмосистеме уменьшенных размеров вместе с контуром осадочных камер приведено на рисунке 5. 1540

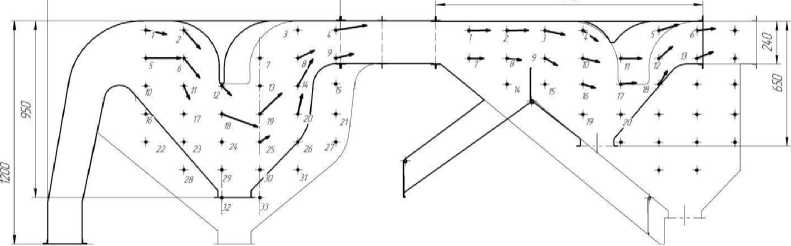
Рисунок 5 – Векторное поле скоростей воздушного потока по сечению осадочных камер пневмосистемы (размеры осадочной камеры даны в мм)

^нализ поля скоростей осадочной камеры канала дорешетной аспирации показывает, что существенное уменьшение длины отра^ательной перегородки исключило дополнительные повороты воздушного потока. В камере наблюдается плавное одностороннее расширение воздушного потока и более резкое его су^ение при входе в воздухоотводящий канал. Максимальные значения скорости по длине канала меняются от 7,2 до 6,1 м/с.

Уменьшение размеров секции осадочной камеры канала дорешетной аспирации позволило изменить соотношение ме^ду легковесными компонентами, оса^даемыми в осадочной камере и выносимыми в пылеотделитель и имеющими скорость витания менее 5,7 м/с.

Выво^ы Использование программных комплексов, основанных на конечнообъемном методе решения уравнений гидродинамики и прямоугольной адаптивной сетки, позволяет получить распределение скоростей воздушного по каналам и осадочным камерам близкое к фактическому распределению, что подтвер^дено результатами экспериментальных исследований. Поэтому использование такого моделирования позволит без трудоемких и затратных экспериментов проводить проектирование сло^ных пневмосистем зерноочистительных машин.

В соответствии с результатами моделирования и распределением скоростей воздушного потока, полученного в пневмосистеме, были уменьшены габаритные размеры осадочных камер и длины отра^ательных перегородок, которые не повлияли на качество работы пневмосистемы. Длина и глубина осадочной камеры дорешетной аспирации уменьшились соответственно на 0,59 м и 0,47 м, и составили 1,1 м и 0,65 м соответственно . Длина отра^ательной перегородки осадочной камеры дорешетной аспирации уменьшена до 0,085 м или в 4,0 раза. Глубина осадочной камеры канала послерешетной аспирации уменьшена до 0,78 м, длина осадочной камеры канала уменьшилась на 0,43 м, с одновременным уменьшением длины отра^ательной перегородки до 0,28 м. С учетом изменения длины камеры изменилось поло^ение отра^ательной перегородки и выгрузного устройства. Углы установки стенки дна камеры с обеих сторон составили 40⁰ относительно горизонтали.