Применение критериев динамического качества для оценки работоспособности зубчатых передач

Введение. Повышение качества машин и их важнейших составных частей – систем приводов, требует при проектировании учитывать динамические процессы, неизбежно возникающие в работе технологических машин. Эти процессы проявляются в форме колебаний инерционных масс на упругих элементах привода, вызывающих увеличение нагрузок в звеньях и кинематических парах, снижающих характеристики надежности и экономические показатели машины.

В настоящее время актуальной становится задача создания эффективного импортозамещающего оборудования для производства деталей (трубопроводов в ракетостроении, рессор автомобильного транспорта, обслуживающего данную отрасль, и др.) из отечественного сырья. Восстановление и ремонт деталей достаточно затруднителен, а покупка импортных комплектующих обходится дороже.

Все это позволит сократить себестоимость в 3–5 раз. Существует потребность в данном технологическом оборудовании. Основные преимущества этого оборудования – это простота в изготовлении, высокая надежность и относительно малая стоимость при мелкосерийном производстве.

В данный момент на существующем рынке нет предложений по данному виду оборудования для использования его в небольших автосервисах, малых предприятиях, а также в технопарке при ремонте и обслуживании технологических транспортных машин и другого оборудования как в полевых, так и стационарных условиях, а также для гибки труб различного поперечного сечения, необходимых для ракетостроения.

При разработке станка для рихтования и проката рессор, удовлетворяющих современным требованиям, был проведен патентный поиск и были обнаружены авторские свидетельства на аналогичное оборудование [1–3].

На этапе эскизного проекта была разработана оригинальная конструкция станка для рихтовки рессор (рис. 1), обладающая небольшими габаритами, технологичностью изготовления и относительно небольшой стоимостью. Данные характеристики станка позволяют без особых усилий перевозить его с одного места на другое, что может быть удобно при обслуживании на выездных полигонных испытаниях различных ракетных установок.

Также была выполнена разработка динамической модели привода станка, учитывающая совместное действие крутильно-поперечных колебаний на этапе эскизного проектирования и оценки динамических характеристик для исключения влияния вибрационных колебаний на качество рихтовки по разработанной ранее методике [4–8].

Одним из элементов в этой динамической модели является зубчатая передача. Зубчатые передачи ши- роко используются в механических приводах космической техники (приводы раскрытия антенн, поворотные механизмы антенн и т. п.). Для механических приводов космической техники при проведении агрегатных испытаний одним из критериев работоспособности является вибропрочность. В результате этих испытаний выполняется частотный анализ в момент запуска и эксплуатации, соответственно, предложенную методику можно использовать и при расчёте приводов космической техники.

Рис. 1. Опытный образец конструкции станка для проката и рихтования рессор

Данная работа направлена на разработку методики расчёта динамических характеристик и анализа динамического качества зубчатых передач на этапе эскизного проектирования, учитывающей как крутильные, так и поперечные колебания в механической системе.

Разработка динамической модели станка. При проектировании оценку динамического качества привода обычно выполняют на стадии технического или рабочего проекта, когда уже созданы электронные твердотельные модели деталей и сборок. При этом используется метод электронного моделирования в САПР – CAE-системах типа MSC/NASTRAN, ADAMS (MDI) и др.

На стадии синтеза схемных решений и выполнения эскизного проекта привода необходимы методики и программные продукты более простого типа. Они должны позволять с помощью ЭВМ давать оценку принимаемым проектным решениям: выбрать лучшую по динамическим показателям конструкцию из ряда рассматриваемых вариантов или сопоставить полученные значения показателей с установленными нормами.

Большинство механических приводов технологических и транспортирующих машин являются многозвенными. В общем случае для оценки динамики разрабатываемой конструкции привода необходимо использовать уравнения движения с большим числом обобщенных координат. Применение упрощенных двух- и трехмассовых приведенных динамических моделей приводов не даст достаточной информации для совершенствования конструкции.

Существующие упрощенные методики и программы оценки динамических характеристик приводов, как правило, основаны на рассмотрении лишь крутильных колебаний в системе, т. е. динамики одномерных систем. Между тем, в реальных системах приводов наряду с крутильными колебаниями возникают колебания инерционных масс в поперечном и продольном (по отношению к осям валов) направлениях вследствие деформаций валов и подшипниковых опор. Более полная оценка динамического качества привода требует рассмотрения его многомерных систем с увеличенным количеством обобщенных координат.

Многомерные модели для расчета поперечных, из-гибных и других видов колебаний разработаны лишь для отдельных элементов приводов (шпиндели металлорежущих станков, ступенчатые валы). Предложенный К. В. Аугустайтисом [9] метод расчета крутильно-поперечных колебаний с использованием уравнений Лагранжа второго рода с неопределенными множителями и нормальных координат Б. В. Булгакова неприемлем для расчета протяженных систем приводов в силу его трудоемкости и трудности вычислений на начальной стадии проектирования. Этот метод также не учитывает упругости зубчатых и гибких элементов передач, изгибной деформации валов.

В работе К. В. Аугустайтиса [9] рассматриваются модели приводов с зубчатыми передачами, в которых в качестве обобщенных координат приняты углы поворотов колес, расположенных на одном валу, и поперечные колебания каждого колеса (вдоль и поперек линии зацепления) по двум координатам на упругих опорах (рис. 2).

Преимущество данного метода заключается в том, что учитывается нелинейность сил трения и гироскопических сил в системе привода. Для этой цели он приводит уравнения движения к неклассическим нормальным координатам Б. В. Булгакова. Недостатком метода является то, что податливость в зацеплении зубчатых колес взаимодействующих валов не учитывается, а матрицы системы с применением избыточных координат оказываются заполненными, громоздкими, что затрудняет вычисление собственных значений системы с большим количеством элементов. Не учитываются также поперечные изгибы валов.

Показано, что многомерные системы в ряде случаев целесообразно разделять на одномерные, а результаты расчетов суммировать. Этот перспективный подход к расчетному анализу динамических систем приводов, к сожалению, еще недоработан. Например, нет эмпирических зависимостей для расчета поперечной жесткости муфт, дискретизации распределенных масс валов, методов приведения упругих податливостей валов и опор к узловым точкам моделей.

В работе [10] показано, что параметрические явления при вынужденных колебаниях косозубых зубчатых колес также можно изучать на ЭВМ сведением пары колес (рис. 3) к системе с сосредоточенными параметрами.

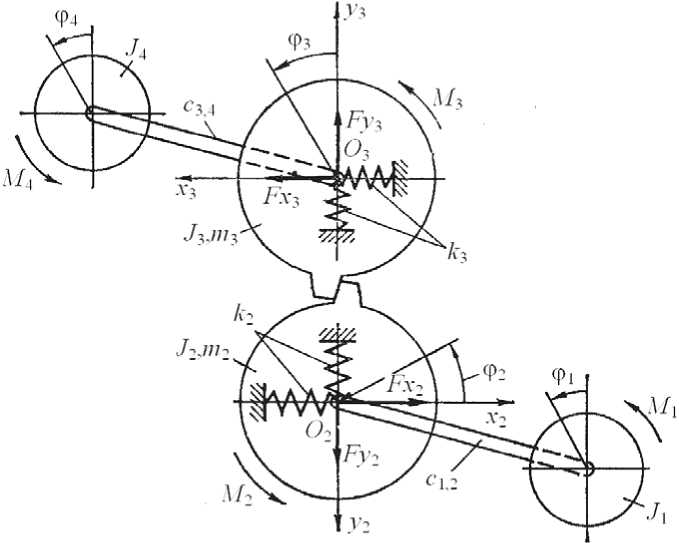
Рис. 2. Динамическая модель двухвальной зубчатой передачи при крутильно-поперечных колебаниях

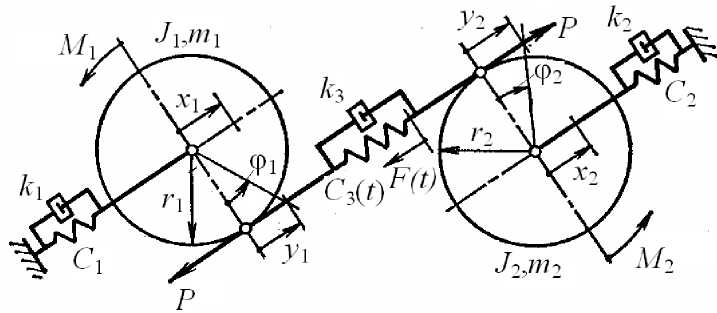
Рис. 3. Динамическая модель пары зубчатых колес при крутильно-поперечных колебаниях

Динамическая модель зубчатой пары должна учитывать поперечные и крутильные колебания колес; система дифференциальных уравнений, описывающих эти колебания, имеет вид m1 x i + k1 (to) x i + k3 (to) x з + C1 x1 + C3 (t) x3 = - F (t), m2 x2 + k2 (to) x2 - k3 (to) xз + C2x2

- C з ( t ) x з = F ( t ),

K1)

J i Ф 1 + k 3 ( to ) R i x з + C з ( t ) R o i х 3 = M 1 - F ( t ) R 01 ,

J2 Ф2 k3(to)Ro2 x3 C3(t)Ro2х3 = M2 + F(t)R02, где x3 = (x1 + φ1R01) – (x2 + φ2R02) – деформация зубчатого зацепления; mi, Ji – массы и моменты инерции колес; Сi – жесткость опор; С3(t) – переменная во времени жесткость зацепления; F(t) – функция силового возбуждения колебаний; ki(ω), k3(ω) – коэффициенты демпфирования в опорах колес и в зацеплении.

Динамическая модель переборного редуктора в случае, когда зубчатые колеса представляются в виде твердых тел, сводится к многомассовой системе, расчет которой с использованием ЭВМ не вызывает принципиальных сложностей. Однако для изучения процессов, происходящих в редукторах, целесообразно отдельно рассмотреть поведение каждой зубчатой пары, заменив связи, наложенные на зубчатые колеса сопряженными с ними деталями, динамическими жесткостями. В тех случаях, когда между деталями существует слабая упругая связь, такое выделение зубчатой пары с заменой динамической жесткости упругой связи ее статической жесткостью не приводит к заметным погрешностям [11; 12]. Однако отнесение упругой связи к слабой требует полного изучения всей динамической модели редуктора. Поэтому целесообразно применять геометрическую интерпретацию колебаний зубчатой пары, поскольку анализ аналитического решения задачи о колебаниях даже простейшего переборного редуктора чрезвычайно затруднителен и приводит к сложным зависимостям.

Заслуживает внимания предложенный Х. Р. Казы-хановым [13] модульный метод формирования динамических систем тракторной техники, исследования и анализа их динамических характеристик. Модульный подход в сочетании с методом конечных элементов позволит упростить расчет и анализ динамических характеристик систем приводов. Для сравнительной оценки вариантов разрабатываемых приводов на начальном этапе проектирования необходимо разработать методики расчета крутильных и поперечных колебаний для схем приводов, составленных из характерных динамических модулей, таких как двигатель, передача, вал на опорах, муфта, нагрузка на выходном звене.

В зарубежных работах известны исследования Кахрамана [14; 15] и Паркера [16], в которых традиционно используются динамические модели с сосредоточенными параметрами [17], в которых зубчатое зацепление представляется в виде жёстких дисков, соединённых упруго-демпфирующей связью.

В многомерных системах механические передачи (зубчатые, с гибкой связью), а также муфты следует рассматривать как конечный элемент с двумя узловыми точками, которые обладают несколькими степенями свободы и соединены между собой упругим звеном.

При крутильных колебаниях зубчатые передачи моделируют в виде системы, состоящей из воспринимающего V и передающего P дисков, связанных податливым элементом – пружиной, имитирующей контактную и изгибную податливость взаимодействующих зубьев. Крутильную собственную податливость зубчатых передач по данным [18] можно определить по эмпирической зависимости e =     K з

ПЗ bR i cos² (a + p),

где K 3 – упругая деформация пары зубьев при действии единичного нормального давления, приложенного на единицу ширины зуба; для стальных прямозубых колес коэффициент контактной податливости K 3 = 6∙10^–11 м²/Н; для стальных косозубых колес K 3 = = 3,6∙10^–11 м²/Н; для шевронных колес K 3 = 4,4∙10^–11 м²/Н. По данным [20] податливость зубьев колес лежит в пределах K 3 = (3,3–5) ∙10^–11 м²/Н, что практически соответствует источнику [5].

Модель конечного элемента зубчатой передачи при крутильных колебаниях можно получить, представив его как двухдисковую систему с упругой безынерционной связью между дисками. При этом моменты инерции дисков должны быть приведены к тому же валу (оси вращения диска), к которому приводится крутильная податливость.

Элементы матрицы жесткости конечного элемента можно определить с помощью выражения потенциальной энергии системы. Если выразить перемещения точки контакта конечного элемента через угловые перемещения колес и радиусы их начальных окружностей, то потенциальная энергия П запишется в виде

2П = K пз ( R ■ф ПР - R 2 ^)², (3) где K _ПЗ = b ∙cos(α + ρ)/ K ₃; α – угол зацепления; ρ – угол трения в зацеплении; ф ПР - приведенный к ведущему диску Р угол закручивания ведомого диска V . Учитывая, что ф ПР = ф ₂ ■ U VP , U_VP = R ₂ / R 1 , из преобразований [19] получим приведенную к диску Р матрицу жесткости передачи:

тактная и изгибная жесткость зубьев не зависит

от межосевого расстояния, имеет вид
		■ c 11   0    c 13   0 "
	[ C ] =	0     c 22 0    c 24 c 31   0 c 33 0	,                 (6)
		_ 0     c 42 0    c 44 _
где с 11 =	с 33 = b cos2γ/ K З , с 13 = с 31		= – b cos2γ/ K З ,
с 22 = с 44 =	R 22 ∙ b cos2γ/ K З , с 24 = с 42 = – R 2 2		∙ b cos2γ/ K З .

Матрица инерции конечного элемента зубчатой передачи, приведенной к валу Р , имеет вид

[ C ] = K пз ■ R 2 ■

- 1

- 1

Полученное выражение согласуется с зависимостью, приведенной в [20].

В двухмерных системах зубчатую передачу следует рассматривать как конечный элемент (рис. 4) с двумя узловыми точками, каждая из которых обладает двумя степенями свободы, т. е. точки V и P имеют степени свободы x V , φ V , x P , φ P ( x V , x P направлены вдоль линии центров колес).

Вектор узловых сил Q и вектор узловых перемещений q в конечном элементе связаны с искомой матрицей жесткости C размером 4×4 соотношением, в котором силы Q имеют разную размерность:

{Q } = [ C ]■{ q}. (5)

Матрица жесткости зубчатой передачи (рис. 4), приведенной к валу Р , учитывая, что диски в зубчатой передаче вращаются в разных направлениях, а кон-

	■ m i	0	0	0 "
[ А ] =	0	2 J 1 UVP	0	0	.               (7)
	0	0	m 2	0
	_ 0	0	0	J 2 _

Относительное демпфирование в зубчатой передаче ψ ≈ 0,15.

Динамические параметры конической зубчатой передачи можно определять по зависимостям цилиндрической передачи, если принять взаимное положение конических колес с условно параллельными валами (рис. 5).

Такая условность позволит рассматривать ортогональные конические передачи в той же плоскости, в которой расположены другие передачи без перехода к повернутым координатам. Предлагаемое условное расположение конических колес не потребует учета осевых сил в их зацеплении. Динамическая модель зубчатой передачи в этом случае будет единой для цилиндрических и конических колес (рис. 4).

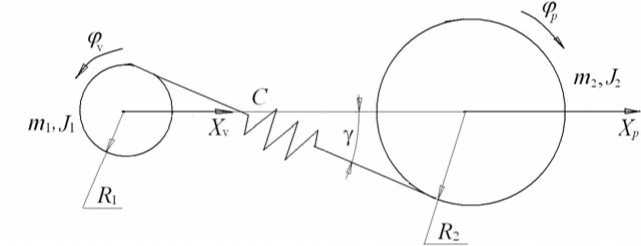
Рис. 4. Двухмерная динамическая модель зубчатой цилиндрической и конической передачи

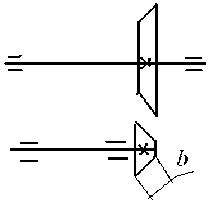
Рис. 5. Условная модель конической передачи при динамическом расчете

Допускаемые значения коэффициентов динамичности

Значение коэффициента динамичности Kdbri	Динамическое качество
	Малые машины. Мощность N < 15 кВт	Средние машины. Мощность N = 15–75 кВт	Тяжелые машины. Мощность N > 75 кВт
0,28	Отличное	Отличное	Отличное
0,45
0,7	Хорошее
1,1		Хорошее
1,6	Удовлетворительное		Хорошее
2,0		Удовлетворительное
4,5			Удовлетворительное
7,0	Плохое
11,0		Плохое

Для стальных прямозубых конических колес коэффициент контактной податливости можно принять, как и для цилиндрических, K З = 6∙10^–11 м²/Н; для стальных конических колес с криволинейным зубом K З = 3,6∙10^–11 м²/Н.

Расчет динамики зубчатой передачи разрабатываемого станка. Исходные данные для расчёта: масса зубчатого колеса m 2 = 6,55 кг; масса шестерни m 1 = 3,38 кг; угол зацепления α = 20^о; ширина зубчатого венца b = 0,05 м; радиус зубчатого венца шестерни по делительной окружности R 1 = 0,054 м; радиус зубчатого венца колеса по делительной окружности R 2 = = 0,084 м; момент инерции шестерни J 1 = 0,0054 кг/м²; момент инерции колеса J 2 = 0,025 кг/м²; коэффициент контактной податливости Kz = 6∙10^–11 м²/Н; передаточное число зубчатой передачи U_VP = 1,55.

Матрица жесткости (6) в числовом представлении:

	" 7,4 - 10s	0	- 7,4 - 10s	0     1
	0	2,1 - 106	0	- 5,2 - 106
[ C ] =	- 7,4 - 10s		7,4 - 10s
		0		0
	_ 0	- 5,2 - 106	0	5,2 - 106 _

Матрица инерции (7) в числовом представлении:

	" 3,38	0	0	0 "
[ А ] =	0	0,061	0	0
	0	0	6,55	0
	[ 0	0	0	0,054 J

Из уравнения (5) получили собственные частоты поперечных колебаний вала f 1 = 0,016 Гц; f 2 = 21,452 Гц, собственную частоту крутильных колебаний вала f 3 = 26,368 Гц.

Для оценки динамического качества зубчатой передачи используется коэффициент динамичности Kdbr_i [11]:

Kdbr, =

QiA ( ^W 0 i ) QiA ( 0 )

Полученные коэффициенты: Kdbr 1 = 0,5 ; Kdbr₂ = = 2,407 - 10 ^{- 4}; Kdbr₃ = 0,5.

Вычисленные значения коэффициенты динамичности сравнивают с допускаемыми (нормативными) значениями, представленными в таблице.

Сравнивая полученные коэффициентов динамичности, можно увидеть, что динамическое качество зубчатой передачи хорошее как для поперечных колебаний, так и для крутильных.

Заключение. При разработке конструкции механического привода на начальном этапе эскизного проектирования, используя предложенную методику составления динамической модели конечного элемента зубчатой передачи и расчёта её динамических характеристик, возможно быстро оценить динамическое качество передачи как отдельно, так и в составе привода, включая космические аппараты, с целью улучшения динамики конструкции привода.