Применение критериев подобия для оценки электромагнитной совместимости частотных электроприводов с системой электроснабжения промышленных предприятий

QF2

AVVG 4х95 70м

QF6

6кV

VNA-10/630 U2

АPVBbShV 3х120 50м

QF9

AVVG 4х50 25м

AVVG 4х25 25м

TV 630/6/0,4

1600А

QF3

QF5

QF4

1PC

QF7

AVVG 4х95 70м

AVVG 4х95 75м

Generalized Load

=r

QF10

VVG 4х4 20м

QF8

AVVG 4х120 120м

QF1

VVG 4х50 25м

AVVG 4х16 70м

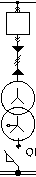
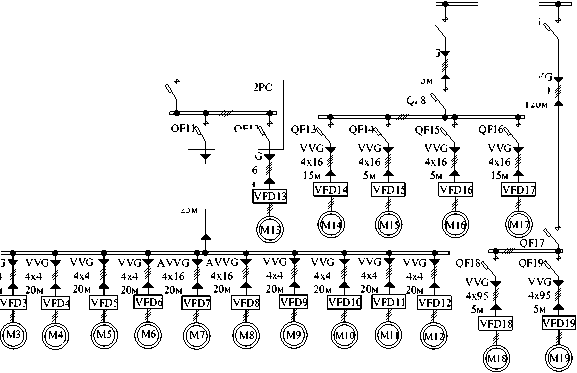
Рис. 1. Схема системы электроснабжения промышленного предприятия по производству железобетонных изделий

Fig. 1. Scheme of the power supply system of an industrial enterprise for the production of reinforced concrete products позволяют получать результаты с высокой степенью достоверности, но они фиксируют ситуацию только на момент измерений и при определенном режиме данного технологического процесса; физическое моделирование представляет собой метод исследования свойств определенного объекта посредством изучения свойств другого объекта, более удобного для решения задач исследования и находящегося в определенном соответствии (подобии) с первым объектом.

При решении задач в общем случае под физическим моделированием понимается изучение моделируемого объекта, базирующегося на взаимно-однозначном соответствии определенной части свойств оригинала и замещающего его при исследовании объекта, и включающее в себя построение модели, изучение ее и перенос полученных сведений на моделируемый объект-оригинал [4].

Суть метода физического моделирования основывается на теории подобия, которая представлена тремя теоремами. Основные положения этих теорем определяют свойства подобных объектов исследования и указывают требования, при удовлетворении которых один из объектов может рассматриваться как модель по отношению к остальным. Основной характеристикой подобных объектов являются критерии подобия, с помощью которых устанавливается взаимооднозначное соответствие модели и оригинала. Критерии подобия – это идентичные по форме алгебраической записи для подобных объектов безразмерные степенные комплексы определенных групп параметров, характеризующих эти объекты [5].

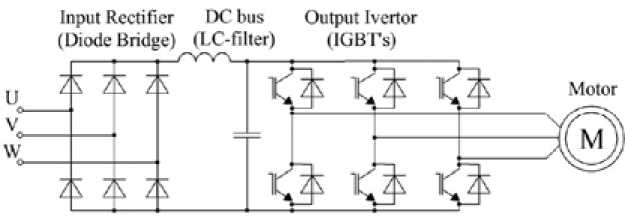
Рис. 2. Cиловая часть принципиальной схемы частотно-регулируемого электропривода

Fig. 2. Power circuit diagram variable frequency drive motor

В качестве объектов подобия принята силовая часть принципиальной схемы ЧРЭ (рис. 2) как источника высших гармонических составляющих тока и напряжения. Правомерность использования критериев подобия подтверждается соответствием динамических процессов в ЧРЭ малой и большой мощности. Исходными при описании физических процессов в ЧРЭ являются дифференциальные уравнения отдельных элементов силовой части: неуправляемого выпрямителя (НВ), промежуточного звена постоянного тока (ПЗПТ), автономного инвертора напряжения (АИН) и асинхронного двигателя с короткозамкнутым ротором (АДсКЗ), отражающие интересующие информационные свойства объекта.

Согласно первой теореме для составления π-критериев подобия параметров применим метод структурного моделирования. Выделив в качестве отдельных элементов TV, АИН, НВ, ПЗПТ и АДсКЗ, запишем уравнения напряжений в дифференциальной форме для трансформатора и обобщенную систему уравнений каждого элемента двухзвенного преобразователя частоты в системе подвижных координат [ u;u ], являющихся основополагающими для объекта-оригинала [6].

fu

di1

u = r • i + L •+ L

1    1 1    11 dt 12

u2

r2 i2

^^^^^в

•

u

u

*

u uf

2 • U0 ’^Ju

= u , вu

u υ

u = (u в 2 вu

di u в в

dt

u, =

1u d у

0 =---

L22

* u

υ

•

di2 dt

di2 dt

^^^^^в

L

•

di1 dt

² ’ U0

,u

иu

= u

и

• f , u u иυ

= u • f ,i = — (i, • f + i, • f ); и υ и 2 1u u 1υ υ

= u , f вυ вu

• f + u вu

вυ

^^^^^в

L рф dψ 1u

u и

,

du и dt

в

dt

2u

в

dt

2 • 43

π

• f ), i вυ u

i с

С бф

, iс

ωψ k 1υ

ю у k1 2 и

в

+

Ri

1 1u

cos θ , f i вυ

2 • 43

π

sin θi;

= i

в

= i

в

^{, u} 1U

• f , i = i • f вu υ в вυ

- i ; и

d у 1

1u dt

в

;

M = —p у i.

2 r п4 0u 1u

в

ю у + R,i , 0 = э1 2и     2 2u

— P У У , 2 гп 4 0 и 1u

d ю ю у, + R.i. , J---э = M - M ; k4 1u 1 1u dt             c

d у

---2^- + ю у dt k 2u

в

ю у + Ri ; э1 2u 2 2и

где u₁, i₁ – мгновенные значения напряжения и тока первичной обмотки; u₂, i₂ – мгновенные значения напряжения и тока вторичной обмотки, приведенные к первичной; r 1 , r₂, L 11 , L 22 - активные сопротивления и собственные индуктивности обмоток; L 12 , L 21 - взаимная индуктивность обмоток; u *u , u * _D - преобразованные задающие воздействия; f_u, f_D - усредненные коммутационные функции (индекс модуляции); U₀ – амплитуда опорного сигнала; u_и – напряжение источника питания инвертора; i_u - усредненный ток питания инвертора; и_ии, и_ио - усредненные выходные напряжения инвертора; i_1u, i_1v - усредненные выходные токи инвертора; u_u, u_v, i_u, i_D - преобразованные основные гармоники напряжений на силовом входе неуправляемого выпрямителя и токов сети; f_6u, f_6C - преобразованные основные гармоники коммутационных функций неуправляемого выпрямителя; 9 i - угол поворота обобщенного вектора коммутационной функции выпрямителя, или результирующего вектора тока сети, относительно оси фазы А напряжения сети; и в , i_e - напряжение и ток на выходе выпрямителя; L_р ф - индуктивность сглаживающего реактора LC-фильтр; С_б ф – емкость конденсаторной батареи фильтра; i c - ток конденсатора фильтра; u_1u, u_1o, i_1u, i_1D1 y_lu, y_Jc - соответственно преобразованные напряжения, токи и полные потокосцепления обмотки статора; i_2u, i_2c, ^_2u, ^_2d - преобразованные токи и полные потокосцепления обмотки ротора; ψ 0u , ψ 0ʋ – главное потокосцепление; р_п – число пар полюсов.

На основе теоремы о подобии сложных систем, состоящих из подсистем, и используя правило Фурье, определим критерии подобия путем приведения уравнений к безразмерному виду, а именно способом интегральных аналогов [4]. При этом сопоставляемые процессы в объекте-оригинале и объекте-подобии подобны, поэтому между их сходственными параметрами должны существовать соотношения пропорциональности, например для ПЗПТ (уравнение 1), (параметры модели подобия обозначаются теми же буквами, но со штрихами):

i с

=m i с

⋅ i ; c

i =m ⋅i ; i =m ⋅i , в iв и iи ви

где m i – масштабные коэффициенты.

Подобие процессов в оригинале и объекте-подобии означает, что они, имея качественно одинаковый характер и различаясь лишь масштабами, должны описываться одинаковыми математическими уравнениями. Это возможно только в том случае, если будут равны единице комбинации масштабных коэффициентов при соответствующих членах однородного уравнения, например для ПЗПТ:

Iπ1

u в ⋅ t ⋅ L ′ рф ⋅ i ′ в

I

u′ ⋅t′⋅L       ⋅i в рф в iс ⋅t⋅C′бф ⋅u′и

1;

π 2

u и ⋅ t ⋅ L ′ рф ⋅ i ′ в

u ′ и ⋅ t ′⋅ L _рф ⋅ i в

1;

i ′ _с ⋅ t ′⋅ C _бф ⋅ u _и

1;

I π 4

i _в ⋅ i ′ _с

′ в ⋅ i с

1;I π

i _и ⋅ i ′ _с

i _и ⋅ i _с

Критерии подобия трансформатора и ЧРЭ (по правилу интегральных аналогов) получены путем приведения уравнений к безразмерному виду:

• • трансформатор:

  	L ⋅ i           L ⋅ i             u π 1 = ⋅ i ⋅ t ;   π 2 = r ⋅ i ⋅ t ; π 3 = r ⋅ i ; r 1   1                     1 1                    1 1                                                   (4) π = - L 22 ⋅ i 2; π = - L 21 ⋅ i 1; π 6 = - u 2 ; 4       r 2 ⋅ i 2 ⋅ t 5       r 2 ⋅ i 2 ⋅ t                 r 2 ⋅ i 2
  АИН:	0.5 ⋅ u *           0.5 ⋅ u            u ⋅ f π =       u ; π =       υ ; π = и u ; 7    U 0 • f.        U 0 ' f u           “-                             (5) u и ⋅ f υ            1.5 ⋅ i u ⋅ f u            1.5 ⋅ i 1 υ ⋅ f υ 10       u и υ ; π 11 =       i и       ;     12           i и        ;
  НВ:	u          u         1.103 ⋅ cos θ       1.103 ⋅ sin θ
  π 13	=   в u ; π 14 =   в υ ; π 15 =                ; π 16 =                ; u             и                 /в u                     f ви                      (6)
  π 17	1.5 ⋅ u в u ⋅ f в u              1.5 ⋅ u в υ ⋅ f в υ              i в ⋅ f в u               i в ⋅ f вυ =               ; π 18 =        u        ; π 19 = i ; π 20 = i ; в                                 в                            uυ
  ПЗПТ:	u ⋅ t                u ⋅ t                  i ⋅ t                 i               i
  π 21	-   •    ; п 22 = и . ; П 23       с       ; п 24 = и ; п 25 = - ;    (7) L рф ⋅ i в             L рф ⋅ i в             C бф ⋅ u и             i c             i c
  АД:	= ψ 1 u        = u 1 u      = ψ 1 υ ;      = u 1 υ 26     R 1 i 1 u t      27     R 1 i 1 u    28    R 1 i 1 υ t     29    R 1 i 1 υ ψ 2 u        ω э ψ 2 υ       ψ 2 υ         ω э ψ 2 u ^ 30            ; ^ 31              ^Х)    ~      ;    ^ 33            ■             (8) 30    R 2 i 2 ut     31     R 2 i 2 u ; 32     R 2 i 2 υ t      33     R 2 i 2 υ ; u                 u υ                  υ π = p п ψ 0 ui 1 υ   π = p п ψ 0 υ i 1 u    π = J ω э ; π = Мс π 34 = М ; π 35 = M ;    36 Мt ; 37 M .

Подобие сложных систем (ЧРЭ), состоящих из подсистем (НВ, ПЗПТ, АИН и АД), соответственно подобных в отдельности, обеспечивается подобием всех сходных элементов и связей, являющихся общими для этих подсистем.

Рассмотрим два электропривода на базе ППЧ-АД (ATV71U22M3-АИР80В4Б01 и VFD1100CH43A-4A160S4У3), технические характеристики и параметры представлены в табл. 1.

На рис. 3 представлены механические характеристики ЧРЭ, полученные опытным путем при частотах 30; 40; 50 Гц, на выходе АИН: а) – ATV71U22M3 b) – VFD1100CH43A(I) и с учетом масштабных коэффициентов m _m = 2.081, m_M= 35.24 и критериев подобия (II).

Как следует из рис. 3 b , механические характеристики ЧРЭ, полученные в результате применения критериев подобия, показали хорошую сходимость с экспериментальными механическими характеристиками, что говорит о правомерности использования критериев подобия для оценки динамических процессов ЧРЭ различных мощностей. Таким образом, использование рассмотренной методики позволяет на основании исследуемого образца (оригинала) пере-

Таблица 1. Технические характеристики и параметры частотно-регулируемого электропривода

Table 1. Technical characteristics and parameters variable frequency drive motor

Тип АД АИР80В4Б01 4A280S2У3 Тип ППЧ ATV71U22M3 VFD1100CH43A Р, кВт 1.5 110 S, кВA 3.5 167 n0, об/мин 1435 2970 Uл, В 380 380 ψ1u 0.0626 0.218 Iном, А 3.7 220 ψ1ʋ -0.903 -0.967 uи, В 589.8 589.8 R1, Ом 7.403 0.05 ic, А 3.77 290.1 i1u, А 3.7 147.984 Сбф, мкФ 620 6100 i1υ, А -2.66 -13.66 Lрф, мГн 0.804 0.042 u1u, В 311 311 u1υ, В 311 311 ψ2u -0.081 0.117 ψ2ʋ -0.854 0.012 R2, Ом 4.257 0.027 i2u, А -3.69 -133 i2υ, А 0.349 1324 ψ0u 0.006 0.176 ψ0ʋ -0.86 -0.572 рп 2 1 t, c 1 1 M, Н·м 10.1 350 Mc, Н·м 7.1 245 J, кг·м2 0.0033 1.1 ωэ, рад/с 157 314 носить результаты оценки аналогичных физических процессов ЧРЭ с одного исследуемого электропривода на другой при различных мощностях двигателя, но при одинаковых режимах работы.

Так как процесс генерирования высших гармоник в ЧРЭ не зависит от мощности электропривода, а определяется только параметрами НВ частотного преобразователя, поэтому предлагаемая оценка масштабных коэффициентов и критериев подобия аналогична для оценки основных показателей ЭМС. Инженерный метод расчета составляющих гармонического спектра позволяет определить действующее значение высших гармоник тока и напряжения при работе преобразователя [7]:

3 ⋅ n ⋅ x

I ( n ) i =        ^{m ⋅ SПРi}       ⋅ sin ϕ i ⋅ sin(       ^{* Σ i} ) ,                                   (9)

• 3 ⋅ π ⋅ U _л ⋅ x _{Σ i} ⋅ n ^{2               m ⋅ sin ϕ} i

*

x_Ci              3 ⋅ n ⋅ x _{Σ i}

U ( n ) i = ^m ⋅ U л ⋅ ^* ⋅ sin ϕ i ⋅ sin(       ^* ) ,                                          (10)

π ⋅ n      x Σ i            m ⋅ sin ϕ i

*

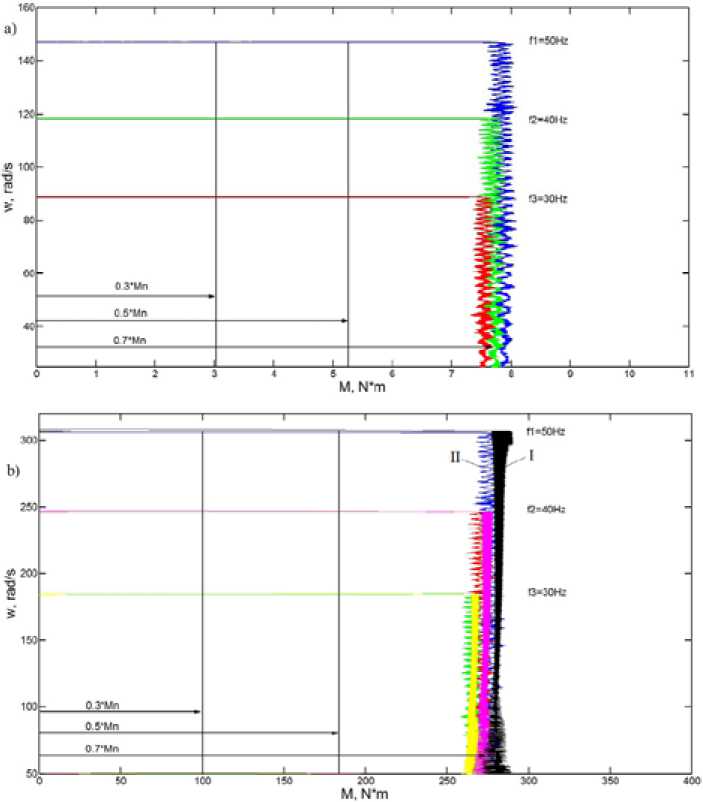
Рис. 3. Механические характеристики частотно-регулируемого электропривода

Fig. 3. Mechanical characteristics of variable frequency drive motor где m - число фаз выпрямителя (m=6); ил - линейное напряжение сети; X% - суммарное ин

*

дуктивное сопротивление одной из ветви цеховой системы электроснабжения, в которой есть электроприемник с нелинейной вольтамперной характеристикой; n – номер канонической гармоники; smф_i - коэффициент реактивной мощности; x а - эквивалентное сопротивление _*

системы в относительных единицах, т.е. сопротивление от условной точки сети бесконечной мощности до точки сети, в которой определяется суммарный коэффициент гармонических составляющих.

Критерии подобия и масштабные коэффициенты определены для действующего значения тока и напряжения любой гармоники в цепи преобразователя (по правилу интегральных аналогов), путем приведения уравнений к безразмерному виду:

π 38( i )

3 ⋅ n ⋅ x _{Σ i}

SПРi    ⋅sin( * ) , xΣi ⋅ I(n)i       m ⋅sinϕi

*

π 39( i )

U ( n ) _i ⋅ x _{Σ i}

*

3 ⋅ n ⋅ x _{Σ i} ⋅ sin( ^* ) , m ⋅ sin ϕ _i

где I ( n ) i , U ( n ) i - действующее значение высшей гармоники тока и напряжения соответственно.

На рис. 4 представлены гистограммы высших гармонических составляющих тока и напряжения с указанными K , и K U в %. Красный и синий цвета относятся к ATV71U22M3 и VFD1100CH43A соответственно и получены опытным путем, а желтым цветом отмечены гистограммы, полученные с помощью критериев подобия масштабных коэффициентов для исследовательской модели.

Гистограммы на рис. 4 подтвердили корректность применения критериев подобия и масштабных коэффициентов для оценки высших гармоник, расхождение экспериментальных и критериальных данных не превышает 5 %.

Выводы

• 1.    На промышленных предприятиях для реализации технологического процесса широко используются рабочие механизмы с ЧРЭ с широким диапазоном мощностей. При этом если в качестве преобразователя частоты используются полупроводниковые преобразователи с промежуточным звеном постоянного тока, то независимо от типов и установленных мощностей физические процессы по генерированию высших гармоник токов и напряжений идентичны.Поэтому для оценки показателей ЭМС предложено использовать критерии подобия и масштабные коэффициенты, позволяющие на основании экспериментальных, аналитических результатов оценки показателей ЭМС одного электропривода трансформировать результаты на все остальные.

• 2.    Полученные критерии подобия и масштабные коэффициенты на основании однотипной записи дифференциальных уравнений для всех элементов ЧРЭ с использованием трех теорем подобия позволяют исследовать и количественно оценивать весь спектр высших гар -моник токов и напряжений, однотипных ЧРЭ с различной установленной мощностью и параметрами питающей сети.

• 3.    Корректность применение критериев подобия и масштабных коэффициентов для оценки показателей ЭМС произведена на серии ЧРЭ различных мощностей. Например, для ЧРЭ с установленной мощностью двигателя Р _н = 1.5 кВт и Р_Н = 110 кВт были измерены и аналитически рассчитаны показатели ЭМС и уровни высших гармоник токов и напряжений, затем эти же показатели для ЧРЭ с двигателем Р_Н = 110 кВт были определены на основании критериев подобия и масштабных коэффициентов на основе показателей электропривода с двигателем Р_Н = 1.5 кВт. Расхождение результатов между натурными экспериментами и полученными на основании критериев подобия не превысили 5-18 % для 5-й и 7-й гармоник и 5 % для коэффициентов суммарных гармонических составляющих по току и напряжению.

  

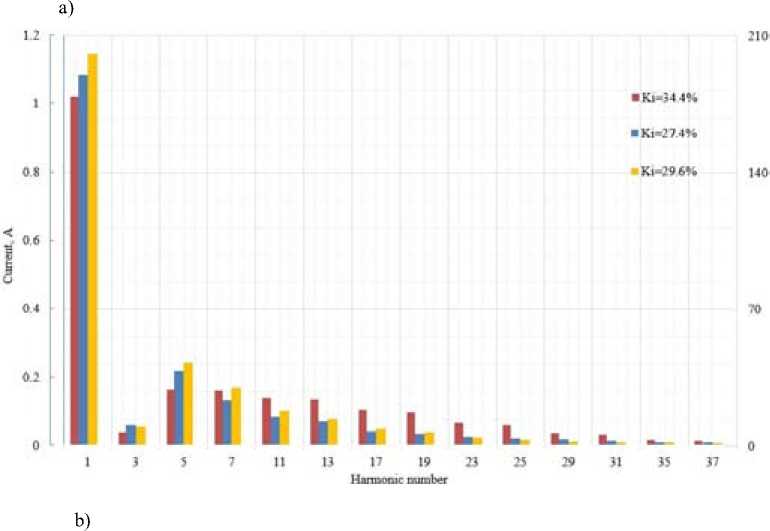
Рис. 4. Гистограмма высших гармоник: а) тока; b) напряжения

• Fig.4. Histogram higher harmonics: a) of the current; b) of the voltage