Применение кривых второго порядка для конструирования гладких каркасно-сетчатых поверхностей

В практике архитектурного проектирования большое значение имеют способы конструирования поверхностей с использованием кривых второго порядка в качестве основных формообразующих элементов [1].

Постановка задачи . Сконструировать гладкую (всюду дифференцируемую) поверхность, опирающуюся на плоский четырехугольный контур и касающуюся боковых граней пирамиды или призмы, построенной на этом контуре как на основании. Иначе говоря, требуется сконструировать поверхность (оболочку), вписанную в данную четырехугольную пирамиду или призму, и касающуюся ее граней вдоль линий заранее заданного плоского сечения.

Предварительно рассмотрим вспомогательную поверхность «прямой клин», образованную движением прямолинейной образующей по направляющим l 0 и g 0 с плоскостью параллелизма zy , и докажем, что если g 0 – эллипс, то сечение прямого клина плоскостью, параллельной плоскости эллипса g 0 , также будет эллипсом (рис. 1).

Отметим точки 1₀ и 2₀ на пересечении произвольной горизонтальной плоскости z=h с образующими A₀M₀ и B₀N₀ . Из рассмотрения двух пар треугольников AKA₀ , 1H1₀ и AA₀M₀ , BB₀N₀ следует, что AA₀:AA′=BB₀:BB′ , то есть ряд точек A′ , B′ ,… образует эллипс g′ , полученный ортогональным сжатием направляющего эллипса g 0 к плоскости xz . Так как 11 0 =AA′ и 22 0 =BB′ , то ряд точек 1 0 , 2 0 ,…, полученных в сечении клина горизонтальной плоскостью, образует эллипс g , конгруэнтный «сжатому» эллипсу g′ , ч.т.д.

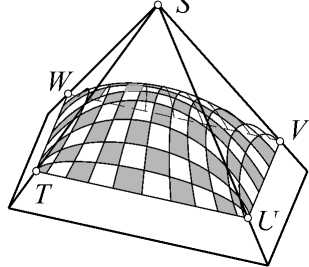
Пусть требуется сконструировать гладкую оболочку на прямоугольном фундаменте TUVW, проходящую через коньковую линию – полуэллипс g0 (полуэллипс – дуга эллипса, ограниченная противолежащими вершинами). Поверхность формируется при параллельном перемещении образующей линии e по направляющей g0. Кривая e, скользя по g0, изменяет свою форму от полуэллипса e0 до прямой TW или UV (рис. 2).

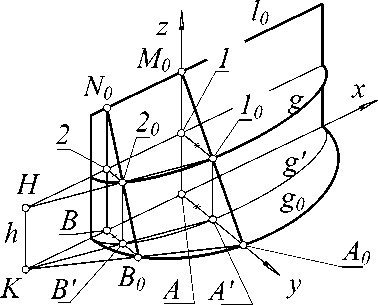
Рис. 1. Прямой клин

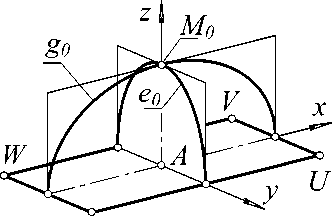
T

Рис. 2. Коньковые линии купола

Поверхность содержит два семейства образующих. Первое семейство состоит из множества полуэллипсов e || zy , опирающихся на стороны TU и VW фундамента. Чтобы найти образующие второго семейства, рассмотрим сечение поверхности произвольной плоскостью, параллельной zx . Покажем, что такая плоскость пересекает сетку кривых e в точках 1 , 2 ,…, лежащих на эллипсе k

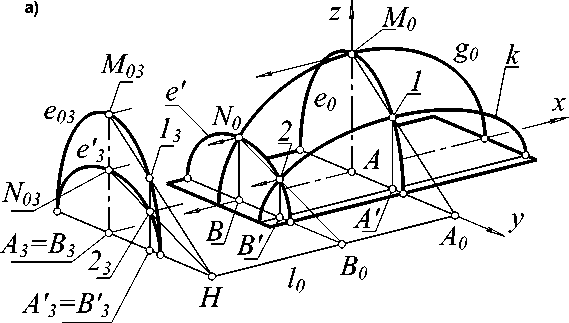
Рис. 3. Купол на прямоугольном фундаменте: а – схема построения, б – аксонометрия

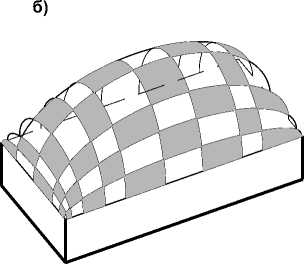
(рис. 3, а). Действительно, проекции e 03 , e′ 3 ,… кривых e₀ , e′ на плоскость, параллельную zy , образуют пучок конических сечений с двумя парами совпавших базисных точек. В этом пучке произвольная коника e′₃ находится в ортогональноперспективном родстве с проекцией e₀₃ конькового эллипса e₀ , поэтому соответственные прямые M₀₃-1 3 , N 03 -2 3 ,… пересекаются в одной и той же точке H на оси родства, проходящей через двойные базисные точки пучка. Кривые e 0 , e′ и их проекции e 03 , e′ 3 конгруэнтны, следовательно, точки A 0 , B 0 , H лежат на одной прямой l 0 , а прямые M 0 A 0 , N 0 B 0 ,… представляют собой образующие прямого клина с направляющими g₀ и l₀ . Но ранее было показано, что в сечении поверхности клина плоскостью, параллельной плоскости направляющего эллипса g₀ , образуется эллипс. Следовательно, кривая k , несущая ряд точек 1 , 2 ,…, является эллипсом. Множество полуэллипсов, параллельных плоскости xz , составляет второе семейство линий каркаса поверхности. Поверхность образована двумя семействами дуг эллипсов, поэтому она может быть названа эллиптическим куполом . Купол плавно сопрягается с вертикальными фундаментными стенами (рис. 3, б).

Покажем, что эллиптический купол на прямоугольном фундаменте описывается алгебраическим уравнением четвертого порядка. Принимая TU = VW = 2 a 0 , UV = TW = 2 b₀ и обозначив высоту купола AM 0 =c 0 (см. рис. 2), запишем уравнение сечения к в виде : x ²/ а ₀ ² + z ²/ с ² = 1, где параметр с ² = Ь2 ( 1- у ² /b 02 ) изменяется от с 0² (при у = 0) до нуля (при у = ± b ₀ ). Подставляя последнее выражение в уравнение образующей k , получаем уравнение поверхности эллиптического купола:

2       2      2       2    2

x y z xy

^{2 ++} 72 - 2Р"

a ₀ b ₀ c ₀ a ₀ b ₀

= 1.

Сечение поверхности плоскостью z = 0 распадается на две пары параллельных прямых: x = ± а , у = ± b , что соответствует форме прямоугольного основания. В сечениях вертикальными плоскостями x=a , y=b ( а <  а ₀ , b <  b ₀ ) получаем два семейства эллипсов с переменным эксцентриситетом. Перемещая начало координат в угловую точку W (см. рис. 2) и пренебрегая в бесконечно малой окрестности этой точки слагаемыми третьего и четвертого порядков малости, получаем вместо уравнения купола уравнение эллиптического конуса z ²/ с ₀ ² = 4 xy/a ₀ b ₀ с осью x=y , z= 0 и вершиной в точке W . Таким образом, в малой окрестности угловой точки поверхность купола близка к конической поверхности второго порядка.

Произвольное проективное преобразование нарушает параллельность прямых и плоскостей, но сохраняет порядок алгебраических кривых [2]. Выполним проективное преобразование, при котором несобственная (бесконечно удаленная) точка пересечения вертикальных ребер фундамента преобразуется в собственную точку S , а основание остается прямоугольным. Такое преобразование сохраняет плавное сопряжение купола с фундаментными стенами, которые из вертикальных становятся наклонными, поэтому купол будет вписан в пирамиду (рис. 4).

Плоскости каркасных линий образуют два пучка плоскостей. Плоскости первого пучка проходят через вершину S пирамиды и несобственную точку G^∞ пересечения противолежащих сторон TU и VW фундамента. Плоскости второго пучка проходят через S и E^∞=UV∩TW . Выполняя произвольное проективное преобразование, получаем куполообразную поверхность, вписанную в неправильную четырехугольную пирамиду (рис. 5). Плоскости семейства каркасных линий e i проходят через вершину S и точку E=TW∩UV , образуя пучок плоскостей ε с осью ES . Плоскости семейства линий каркаса g j проходят через точки S и G=TU∩VW , образуя пучок γ с осью GS .

Короткий В.А., Усманова Е.А.

Применение кривых второго порядка для конструирования гладких каркасно-сетчатых поверхностей

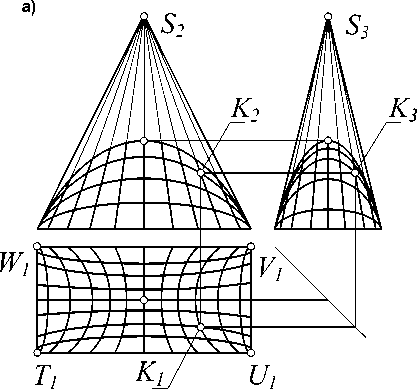
Рис. 4. Купол, вписанный в пирамиду: а – ортогональный чертеж; б – аксонометрия

б)

U

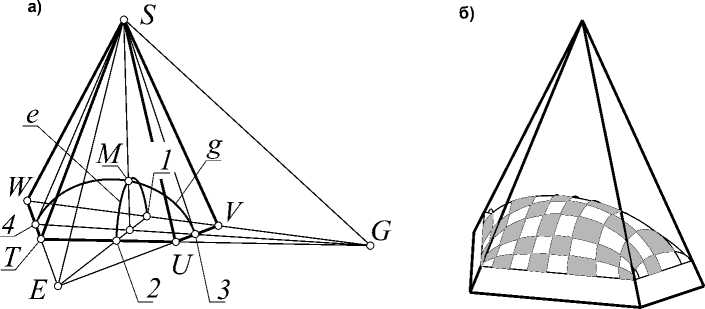
Рис. 5. Купол на четырехугольном фундаменте: а – схема построения; б – аксонометрия

Рассмотрим алгоритм построения купола, вписанного в пирамиду TUVWS и проходящего через данную точку M .

Плоскости пучков ε и γ, инцидентные M , пересекают пирамиду по треугольникам 12S и 34S . Проводим линии каркаса (кривые второго порядка) e и g , проходящие через M , опирающиеся на стороны фундамента в парах точек 12 , 34 и касающиеся сторон треугольников 12S и 34S (рис. 5, а). В произвольной плоскости Σ пучка ε находим линию каркаса e_i , проходящую через точку M i =g∩ Σ и касающуюся сторон треугольника, полученного в сечении пирамиды плоскостью Σ. Множество плоскостей пучка ε индуцирует однопараметрическое семейство кривых второго порядка e i , которые в свою очередь формируют каркас эллиптического купола, вписанного в данную пирамиду. Аналогично формируется второе семейство g j образующих конструируемой поверхности (рис. 5, б).

Произвольная образующая вычерчивается с помощью программы [3] как кривая второго по- рядка, проходящая через три точки и касающаяся двух прямых. Например, кривая e проходит через точки M, 1, 2 и касается сторон S1 и S2 треугольника S12 (см. рис. 5, а).

Заключение. Предложен способ построения гладкой (всюду дифференцируемой) поверхности на прямоугольном или произвольном плоском четырехугольном фундаменте. При использовании предложенного способа обеспечивается плавное сопряжение боковых фундаментных стен с поверхностью купола. Для формирования каркаса поверхности используются только дуги кривых второго порядка. Способ может найти применение в строительстве и архитектуре при проектировании куполообразных оболочек, опирающихся на плоский четырехугольный контур.