Применение кумулянтов при оценивании центральных моментов негауссовского случайного процесса

В настоящей работе рассматривается задача нахождения центральных моментов негауссовского случайного процесса, который моделируется как выходной сигнал нелинейной системы при подаче на ее вход белого гауссовского шума. Таким образом, случайный процесс может быть описан дифференциальным уравнением dx

-^ = a ( t, x_t ) + b ( t ) w ( t ) ,

где w ( t ) – белый гауссовский шум с интенсивностью ^{N 0} .

При заданном распределении начального условия x ₀ требуется определить несколько центральных моментов m 1 ( t ) = Mx t , m k ( t ) = M [ X - m i ( t ) ] k , ( k = ² ,V- , l ) ■

Точное решение указанной задачи при коэффициенте a ( t , x_t ) общего вида возможно лишь в том случае, если известно распределение

Pt (x) = Р {xt ^ x I Po (x)}, где Po (x) = P {xo ^ x} ■

Однако определение аналитического выражения для этого распределения задача трудная,а порой

,    , dPt ( x )

невыполнимая. Так, плотность p (t, x) -—---- dx процесса xt можно было бы вычислить, решив уравнение Фоккера-Планка-Колмогорова dp^lx) = -^Va (t,x) p(t,x)] +

∂t∂x b2 (t) No d2p (t, x)

с начальным условием p (0, x) = dPo ( x )

dx

∂ x ²

, но точ-

ное решение этого уравнения при произвольном a ( t , x_t ) невозможно [1]. В связи с этим актуальное значение приобрели методы приближенного вычисления моментов m _k ( t ) ■

Из приближенных методов наибольшую извест- ность и распространение получил метод статистиче-скойлинеаризации.Этотметодотличаетсяпростотойи зачастую обеспечивает удовлетворительную точность при вычислении первых двух моментов процесса x(t).

В [2] приводится метод неопределенных параметров, который позволяет вычислять моменты случайного процесса с большей точностью, чем при помощи метода статической линеаризации. При этом на основе дифференциального уравнения для характеристической функции процесса x ( t ) выписывается дифференциальное уравнение для начальных моментов. Полученная система уравнений является бесконечной (счетной), и для ее ограничения предполагается задаваться плотностью вероятности p ( t,x ) в виде семейства функций p ( 9 , x ) , где параметр 9 представляет собой совокупность моментов процесса x ( t ) до определенного порядка N включительно. Полученная при этом «урезанная» система из N обыкновенных дифференциальных уравнений для моментов может быть решена численными методами. Однако пренебрежение старшими моментами может приводить к существенным ошибкам.

В [3] приводится метод, основанный на том, что за параметры распределений взяты кумулянты (семиинварианты) вместо моментов. Объясняется это тем, что в противоположность моментам кумулянты не растут с увеличением порядка. Так, например,длянормальногораспределениявсеку-мулянты выше второго порядка равны нулю. Поэтому для распределений близких к нормальному, кумулянты третьего, четвертого и более высоких порядков будут малыми. Это дает возможность аппроксимировать распределения, пренебрегая кумулянтами выше заданного порядка.

В работе на примере случайного процесса, заданного уравнением (1) с кусочно-линейном коэффициентом сноса, будет показано, что если за параметры распределения плотности вероятности взять кумулянты, то погрешность оценки дисперсии будет значительно меньше по сравнению с оценкой дисперсии, рассчитанной по методу статистической линеаризации.

Дифференциальные уравнения для кумулянтов

Пусть x(t) является решением в момент времени t дифференциального уравнения dx

—= = a ( t , x t ) + b ( t ) w ( t ) ■

Известно, что k-й кумулянт случайной вели- Следовательно, для того, чтобы написать диф- чины x(t) в момент t равен X          Лk д ф(t,z) ^ k (t) = ( i)     dzk        ’          (2) ференциальное уравнение для Xk (t); k=1; 2 ... m, необходимо дифференциальное уравнение для ф (t, z), которое в свою очередь можно получить из дифференциального уравнения для f (t, z) ■ z=0 ∞ Как показано в [3] дифференциальные урав- где Ф(t, z) = ln f (t, z) = ln JeizxP (t, x) dx ■ нения для ф (t, z) и f (t, z) соответственно име- -∞ ют вид df (t’z) = /z fe^aU x\p(t x\dx- N0b (t) z^U z) z a t, ^x       t, ^x                        z      t, z , dt4

-∞ дф (t, z)     -ф(t, z). 7 izx                           b2 (t) No 2

—-   = e iz e a(t,x) p(t,x)dx— z dt                 -7 x 7 x '4

Дифференцируя (3) по z k раз, с учетом (2) четырех кумулянтов, приняв гипотезу о том, что можно получить уравнения для кумулянтов. В ка- кумулянты процесса x ( t ) порядка выше четверто-честве примера выпишем систему уравнений для го равны нулю

∞

∂λ ^∞

----= J a ( t , x ) p ( t , x ) dx

∂ t    _-

-∞ b2 (t)No

2      ’

дк

-^- = 2 J ( x -к 1 ) a ( t, x ) p ( t ,x ) dx +

-∞

∂λ ^∞         2

----= 3 J^( x -X] ) -X₂J a ( t , x ) p ( t , x ) d

^{∂ t} -∞ ^⎣⎦

∞

—f = 4 J [ ⁽ x -X i ) -31 2 ( x -X i

) 2 -1 3 I a ( t , x ) p ( t , x ) dx

-∞

Чтобы получить замкнутую систему дифференциальных уравнений относительно кумулянтов, представим плотность вероятности p ( t,x )

тремя членами ряда Эджворда. При этом система уравнений примет вид

~= -CT Lo + 7 ”T (L3 - 3L1) + 77“4 (L4 - 6L2 + 3Lo) , ∂t ⎣6σ24σ⎦

^?A = 2a ² [L + ¹ '(L₄ - 3L) + — " 4 (L₅ - 6L + 3L, )1 + b²^^{t )} N ⁰ ,

∂t     ^⎢⎣ ¹ 6σ ³⁴² 24σ ^{4531 ⎥}⎦2

^{∂λ 3} =3σ ^{3 ⎡} L - L +^{1 λ 3} L -4 L +3 L +^{1 λ 4} L -7 L +9 L -3 L

∂t       ⎢⎣206σ35     3     124σ46     42

^d^ ⁴ = 4 o ⁴ L - L +¹ ^ 3 [- 6L, + L - 6L₄ + 9L₂ + ^ 3 ( 3L - L ) ) +

∂t        ⎢⎣ 316 σ3⎜⎝    0    6     4     2σ313

+ 17 ^T I L 7 - 9 L 5 + 21 L 3 - 9 L 1 + ' ( - 3 L 0 + 6 L 2 - L 4 ) I ,

24 σ⎝σ⎠⎦ где       Lk = J a (oz + X,) zkp (z) dz,

-∞ z2

x ^— Xj *           1      -—    ₂

z =------ , P ( z ) = /----- e 2 , ^ =X 2 .

ст            v2nn ²

Результаты расчетов

Покажем, что вычисление дисперсии случайного процесса x(t) методом, основанным на решении системы дифференциальных уравнений (4) дает более точное значение по сравнению с результатом, полученным методом статической линеаризации.

Пусть случайный процесс задан дифференциальным уравнением dx- = -a (x,) + w (t),             (5)

2 l

^{L 3 =} 2 πσ ²

( 2 +P2 ) exp jj-P-

L 4 = ¹ 1 3Ф ( P ) ^-

2 πσ ²

⎛ ρ ² ⎞⎞

( 3 P + P ) exp I ^- —II ,

^f l , xt — 0

где a ⁽ x t ) = ^

[-l , x t <  0.

Воспользуемся для вычисления дисперсии процесса x ( t ) уравнениями (4). Для этого предварительно вычислим интегралы L_k .

2 l                          ⎛ ² ⎞

^L 5 = I----2 ( ^{8 + 4} P ⁺ P ) exP I ^-— ,

2πσ ²                  ⎝ ² ⎠

^L 0 = ¹ Ф ( P ) ,

2 l

^{L 1 =} 2 πσ ²

exp

L 2 = ¹ Ф ( P ) -

ρ

,

2ρ

₂ exp 2πσ²

ρ

-

,

⎛ 2                           ⎛ ρ ² ⎞⎞

L = l l 15ф ( P ) —      . ( ^I5P ^{+ 5}P ⁺ P ) exp | ^-— | | ,

⎝ 2 πσ                    ⎝² ⎠⎠

L = ^{2 l}   48+24ρ ² +6ρ ⁴ +ρ ⁶ exp - ρ ,

2πσ ²                          ⎝2 ⎠

где

p = —, ф(p) = -erf f-^1.

σ σ ⎝2⎠

После подстановки рассчитанных значений L_k в (4) получим

∂λ

¹ =-σ

∂t

^{1ф ( p})⁺i 4 ж ^{( p} 2 ^- 1) e ² -^ж ^{( p} 3 ^{- 3 p ) e}

∂λ 2 ∂t

-2σ ²

e ² - ³ ρ

2πσ ²      σ32π

^λ 4 l 42^-2

5 I ( P 2p    5 ) e

σ ⁵ 122π

^+N 2 ^{0 ,}

∂λ ₃ ∂ t

= -3σ ³

^{∂λ 4} =- 4 σ ⁴ ∂t

^λ 4     ^l

σ ⁵ 12 2 π

e

2πσ ²

2 l

2 πσ ²

(p

λ ₃ l σ ⁴ 32π

- ^ρ

( 3 + P 4 ) e ²

λ 4     l

σ ⁵ 122π

- ^ρ

( p ^{5 -} 2P 3 +3p ) e ¹

_-ρ ²

- 1 ) e ²

λ l - ^ρ 3 2 ⁺σ ⁴ 32 π ^e

^-P 5 ⁺ P 3 ^{- 6} P ⁺ ^ 3 ( 1 ^- P 2 )

( p 6 ^- 3 P 4 ^- 9 P 2 ^{+ 9} ) ⁺ ^ 3 ( P 3 ^{- 3} P )

Уравнения статистической линеаризации в

В данном примере можно определить точ- этом примере таковы d^1 = -с1Ф (P ), ∂t

∂λ         2l

² =-2σ exp ∂t         2π

-

ρ ² ⎞₊N 0 ₂ ⎟_{⎠ 2}

На рис.1 и рис.2 для случайного процесса, заданного уравнением (1), приведены результаты численного интегрирования систем уравнений (6) и (7) в среде Matlab [5] при следующих параметрах: l = 4, N0 = 4; и начальных условиях: 11 = 0 , x2 = 1, X3 = 0 , x4 = 0 . Вустановившемся состоянии значения дисперсии равны X4 = 0,0077 при учете четырех кумулянтов, X2 = 0,0061 при учете двух кумулянтов.

ность полученного решения, так как в устано- вившемся состоянии плотность вероятности оп- ределяется выражением [6]

2 l ⎛ 4 l ⎞

Ps- ⁽ x ) = 5^^eXP -^lx

N ₀ ⎝ N ₀ ⎠

Используя выражение (8) для плотности, можно вычислить точное значение для дисперсии процесса x ( t ) ∞ 2

X 2 = J ( x ^-Х 1 )² Ps, ( x ) dx = -°- .

8l

-∞

При данных параметрах процесса 1 2 = 0,0078.

Из результатов расчета можно сделать вывод, что ошибка в вычислении дисперсии методом ста- тистической линеаризации составляет 22%, а при учете четырех кумулянтов 1%.

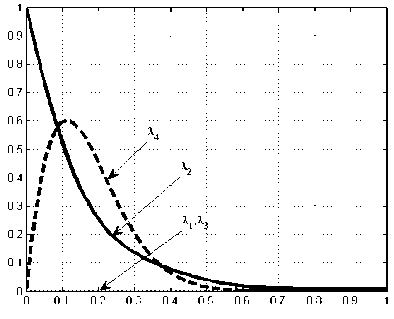
Рис.1. Результаты интегрирования системы уравнений (6)

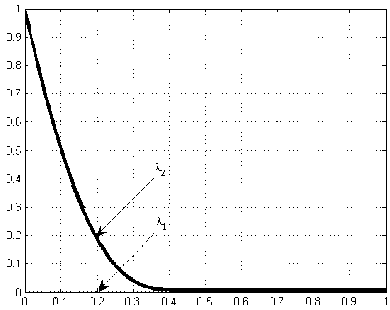
Рис.2. Результаты интегрирования системы уравнений (7)

Вывод

Использование кумулянтов выше второго порядка позволяет повысить точность вычисления центральных моментов. В качестве подтверждения выше указанной гипотезы, на примере случайного процесса, заданного уравнением (5) были определены центральные моменты выходного процесса. Из результатов расчета дисперсии следует, что погрешность вычисления дисперсии методом статистической линеаризации составляет 22%, а при использовании кумулянтов 1%.