Применение кусочно-линейной аппроксимации вероятностно-временных характеристик систем массового обслуживания

Автор: И.Л. Крикунов, К.Э. Гаипов

Журнал: Космические аппараты и технологии.

Статья в выпуске: 4, 2020 года.

Бесплатный доступ

На сегодняшний момент времени от спутниковых технологий в той или иной степени зависят многие современные отрасли. Для построения таких спутниковых систем связи необходима оценка параметров качества обслуживания, одним из которых является время задержки информации. Для реализации математической модели спутниковой сети используются такие аналитические выражения для временных задержек, которые имеют неустранимый разрыв второго рода в момент времени, когда интенсивность поступления трафика становится равной интенсивности обслуживания. Устранение данной особенности позволило бы сократить время расчета оптимальных маршрутов. В представленной работе для достижения поставленной цели используется кусочно-линейная аппроксимация. В качестве способа задания прямых рассматриваются два подхода, которые сравниваются с помощью интегрального метода наименьших квадратов, а также рассмотрен вопрос о количестве используемых прямых в условиях поставленной задачи. В качестве результатов были получены аппроксимационные зависимости, позволяющие построить кусочно-линейную функцию среднего времени ожидания в буфере для системы М/М/1. Описана процедура нахождения оптимальных параметров для данной функции, а также аналитическим методом были получены приближенные формулы нахождения точек касания прямых, зависящие от поступающей интенсивности трафика.

Еще

Спутниковый канал, оптимальная маршрутизация, целевая функция, кусочно-линейная аппроксимация

Короткий адрес: https://sciup.org/14117460

IDR: 14117460 | DOI: 10.26732/j.st.2020.4.04

Текст статьи Применение кусочно-линейной аппроксимации вероятностно-временных характеристик систем массового обслуживания

Актуальность задачи оптимальной маршрутизации заключается в том, что на текущий момент отсутствуют механизмы и протоколы управления трафиком в зависимости от загрузки спутниковых каналов связи.

Под оптимальной маршрутизацией будем понимать такой алгоритм выбора маршрутов между источником и получателем, при котором выполняется условие, что на всех интерфейсах маршрутизаторов и/или коммутаторов будет находиться минимальное число пакетов или суммарное время нахождения пакетов во всех интерфейсах будет минимально, что можно записать в виде целевой функции вида:

F = £ N i ( X ) или F ₂ = £ T i ( X ), где N i (X) - число пакетов на i -ом маршрутизаторе и/или коммутаторе; T i (X) - время нахождения

пакетов на i -ом маршрутизаторе и/или коммутаторе.

Данные задачи были решены в работах Галлагера, Крона, Парфенова, Гаипова, Пономарева и Вишневского [1–8]. Особенностью решения таких задач является то, что каждое слагаемое целевой функции F j и F ₂ является функцией, имеющей разрыв в точке λ = μ, что позволяет решить эту задачу, предварительно решив систему линейных ограничений для определения начальной точки итерации, нужной для численных методов решения задач нелинейного программирования, к которым и относится задача поиска минимума целевой функции.

Решение задачи поиска начальной итерации увеличивает время решения задачи оптимальной маршрутизации, поэтому целью исследования является уменьшение времени нахождения минимума целевой функции. Для этого необходимо решить две задачи:

• устранение разрыва в функциях N i (X) и T i (X) путем выбора оптимального метода аппроксимации;

Kl/IE

АППАРАТЫ И

Том 4
• анализ выигрыша времени и точности найденного решения с первоначальным алгоритмом.

1. Выбор типа аппроксимации

Как было сказано ранее, функциональная зависимость вероятностно-временных характеристик различных систем массового о бслуживания, таких как средняя длина очереди N или среднее время нахождения данных на ожидании t в точке, когда интенсивность поступления данных равна интенсивности их обслуживания, имеет разрыв

²²⁰ второго рода.

В качестве примера приведем функциональ- ную зависимость среднего времени ожидания, из которого явно видно, что при λ=μ имеет место разрыв. Далее в качестве модели, описывающей интерфейс коммутационного устройства, подключенного к спутниковому каналу, будем использовать систему массового обслуживания М/М/1. Данная зависимость имеет вид:

i f (X=

i -

X ^,

µ где μ – скорость работы интерфейса маршрутиза- тора.

Для решения задачи оптимального распределения трафика в качестве критерия, как правило, выбирается сумма средних времен ожидания ∑ t или сумма средних очередей ∑ N . Для нахождения минимума таких целевых функций необходимо вначале найти область определения данной функции и в этой области выбрать точку начальной итерации для применения методов динамического программирования.

Для устранения этапа нахождения точки начальной итерации необходимо устранить разрыв второго рода и сделать так, чтобы функциональная зависимость средней длины очереди или среднего времени ожидания на всей области определения была монотонно возрастающей и выпуклой функцией. Для существующих зависимостей это условие выполняется в интервале [0; μ). Для преодоления этой проблемы в данной работе рассматривается аппроксимация вероятностно-временных характеристик для систем массового обслуживания.

Рассмотрим полиномиальную аппроксимацию. Разложим исходную функцию f(x) в ряд Тейлора. Получаем сумму слагаемых, имеющих вид:

M xi

f(x) пол = £ “’ i=0 Ц где μ – скорость работы интерфейса маршрутизатора, М – количество слагаемых в ряду.

Если использовать этот вид аппроксимации, то он устранит разрыв второго рода, но функция не будет выпукла на всей области допустимых значений, что отображено на рис. 1.

Для кусочно-линейной аппроксимации рассмотрим два подхода, с помощью которых задаются прямые [9]:

• прямая, касающаяся исходной функции;
• прямой, являющаяся хордой исходной функции.

Для выбора наилучшего метода составим уравнения этих прямых для двух подходов, используя две, три и четыре прямые. В качестве критерия оценивания будем использовать ошибку аппроксимации, которая находится по формуле:

y ( i + 1)

⁵ = 2 J [ ^ ⁽ x ) - ^fi ⁽ x ⁾ ^] ² dx ,

iyi где s – ошибка аппроксимации, f(x) – исходная нелинейная функция, fi(x) – кусочно-линейная функция, i – количество прямых в кусочно-линейной функции.

В данном методе ошибка аппроксимации представляет собой сумму интегралов, где под знаком интеграла находится разность исходной и линейной функций [10].

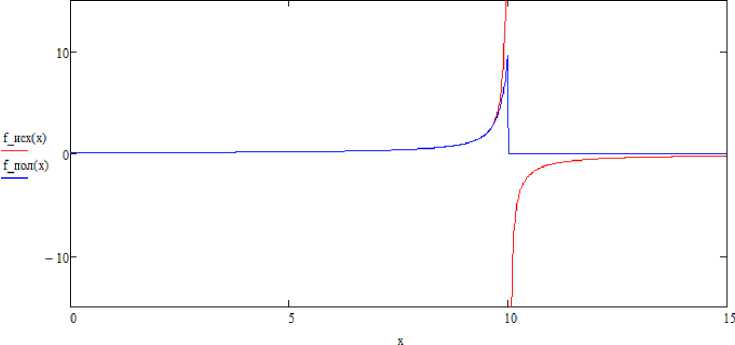
Рис. 1. Графики исходной функции и полиномиального ряда

Расчет ошибки аппроксимации необходимо начать с нахождения оптимальных параметров ( x ₀, x ₁, ..., x_i ) для метода касательных и ( a , b , …, i ) для метода хорд. Под оптимальными параметрами понимаются такие значения, при которых ошибка аппроксимации минимальна для каждого рассмотренного варианта.

В данной задаче ошибка аппроксимации является функцией с множеством локальных экстремумов, т. е. она многоэкстремальная. Аналитическое нахождение минимальных значений приводит к решению систем нелинейных уравнений, что не позволяет аналитически определить все точки экстремума. В связи с этим для нахождения оптимальных параметров данной функции был осуществлен перебор точек начальной итерации для использования метода сопряженного градиента, встроенного в пакет инженерного математического ПО MathCad. Для перебора точек начальной итерации в среде MathCad был исполь- зован алгоритм перебора параметров (x0, x1, ..., xi) для метода касательных и (a, b, …, i) для метода хорд с учетом следующих особенностей:

• каждый следующий параметр должен быть строго больше предыдущего ( x_i _-1< x_i или a < b );
• все параметры для двух методов должны удовлетворять области допустимых значений;
• случаи с отрицательным значением ошибки аппроксимации не должны рассматриваться.

Получив оптимальные значения точек касания и пересечения прямых, необходимо рассчитать значения ошибки при различных интенсивностях поступления трафика. Минимальные зна- ²²¹ чения ошибки аппроксимации и параметров при различных μ представлены в табл. 1.

Из табл. 1 видно, что метод с использованием касательных имеет значительно меньшую ошибку по сравнению с методом хорд при равных условиях. В дальнейших расчетах целесообразно использовать именно этот подход.

Таблица 1

значениях параметра μ

Количество прямых	Касательная			Хорда
Количество прямых	μ = 10	μ = 30	μ = 50	μ = 10	μ = 30	μ = 50
2	s = 18,555	s = 20,894	s = 21,611	s = 9360	s = 9580	s = 9720
3	s = 5,845	s = 6,938	s = 7,311	s = 31,25	s = 68,863	s = 74,105
4	s = 2,612	s = 3,111	s = 3,276	s = 31,2	s = 50,91	s = 62,61

Таблица 2

Зависимость ошибки аппроксимации от числа прямых

Количество прямых	Интенсивность поступления трафика
Количество прямых	μ = 10	μ = 30	μ = 50	μ = 100	μ = 150	μ = 300
2	s = 18,555	s = 20,894	s = 21,611	s = 22,302	s = 22,59	s = 22,933
3	s = 5,845	s = 6,938	s = 7,311	s = 7,695	s = 7,875	s = 8,071
4	s = 2,612	s = 3,111	s = 3,276	s = 3,47	s = 3,568	s = 3,699
5	s = 1,085	s = 1,375	s = 1,489	s = 1,633	s = 1,682	s = 1,797
6	s = 0,566	s = 0,731	s = 0,799	s = 0,879	s = 0,949	s = 1,054
7	s = 0,322	s = 0,422	s = 0,463	s = 0,514	s = 0,56	s = 0,682
8	s = 0,196	s = 0,258	s = 0,286	s = 0,319	s = 0,346	s = 0,42

Таблица 3

Зависимость оптимальных точек касания от интенсивности поступления вызовов

Интенсивность поступления вызовов μ	x ₁	x ₁/μ	x ₂	x ₂/μ	x ₃	x ₃/μ
1	0,4979	0,4979	0,9374	0,9374	0,9819	0,9819
50	35,5196	0,71	49,8869	0,9977	49,9787	0,99957
60	42,976	0,7163	59,8859	0,9981	59,9786	0,99967
70	50,4583	0,72	69,8852	0,9984	69,9786	0,99969
80	57,9804	0,725	79,8845	0,9986	79,9786	0,99973
90	65,5336	0,7282	89,8841	0,9987	89,9785	0,99976
100	73,0281	0,73	99,8839	0,999	99,9785	0,99979
110	80,6379	0,733	109,8834	0,999	109,9785	0,9998
120	88,261	0,7355	119,8831	0,9991	119,9785	0,99982
130	96,1238	0,7394	129,8822	0,9991	129,9785	0,99983
140	104,9985	0,75	139,8867	0,9992	139,9786	0,99985

Продолжение таблицы 3

150	112,997	0,7533	149,8825	0,9992	149,9785	0,99986
160	118,584	0,741	159,8823	0,9993	159,9784	0,99987
170	126,9897	0,747	169,8815	0,9993	169,9784	0,99987
180	134,0347	0,7446	179,8814	0,9993	179,9784	0,99988
190	141,3977	0,744	189,8807	0,9994	189,9784	0,99989
200	149,4555	0,7473	199,8838	0,9994	199,9786	0,99989
250	186,6238	0,7465	249,8811	0,9995	249,9784	0,99991
300	225,12	0,75	299,8793	0,9996	299,9783	0,99993
350	267,2272	0,7635	349,8853	0,9997	349,9787	0,99994
400	296,2645	0,74	399,8788	0,9997	399,9784	0,99995
450	357,1871	0,7937	449,8807	0,9997	449,9785	0,99995
500	380,2357	0,76	499,8759	0,9997	499,9781	0,99996
550	423,258	0,7696	549,8836	0,9998	549,979	0,99996
600	462,816	0,7714	599,8848	0,9998	599,9794	0,99997
650	502,281	0,7727	649,8846	0,9998	649,9792	0,99997
700	541,842	0,774	699,8849	0,9998	699,9794	0,99997
750	581,13	0,775	749,8824	0,9998	749,979	0,99997
800	621,024	0,7763	799,8846	0,9999	799,9795	0,99997
850	660,654	0,777	849,8845	0,9999	849,9745	0,99997
900	700,434	0,7783	899,885	0,9999	899,9799	0,99998
950	740,088	0,779	949,8845	0,9999	949,9794	0,99998
1000	779,88	0,7799	999,885	0,9999	999,9795	0,99998

Kl/IE

АППАРАТЫ И

ных распределений длительности обслуживания и интервалов между вызовами, для удовлетворительной аппроксимации вероятностно-временных характеристик достаточно провести всего лишь три измерения при загрузках 0,77, 0,999 и 0,9999. Для более точной же аппроксимации можно воспользоваться данной методикой для определения большего числа точек, в которых необходимо проводить измерения.

Также необходимо отметить, что переход на кусочно-линейную аппроксимацию хоть и ре-

Том 4

шает проблему устранения разрыва функции, но также приводит и к ряду других проблем, а именно к выбору метода поиска экстремальных значений функций, которые получаются как линейная комбинация и суперпозиция таких функций, т. к. такая задача становится задачей дискретного программирования. Пока же отметим, что в среде MathCAD, даже при использовании стандартной функции miminize , которая использует квазинью-тоновский метод поиска минимума функции, получается небольшой выигрыш при вычислении.

Список литературы Применение кусочно-линейной аппроксимации вероятностно-временных характеристик систем массового обслуживания

Галлагер Р., Бертсекас Д. Сети передачи данных. М. : Мир, 1989. 544 с.
Крон Г. Тензорный анализ сетей : учеб. пособие. М. : Сов. радио, 1978. 720 с.
Парфенов В. И., Золотарев С. В. Об одном алгоритме решения задачи оптимальной маршрутизации по критерию средней задержки // Вестник ВГУ: сер. Физика. Математика. 2007. № 2. С. 28–32.
Пономарев Д. Ю., Гаипов К. Э., Подойницына О. И., Шиянов Е. А. Определение целевой функции для решения задачи оптимального распределения трафика тензорным методом // Труды Международной научно-технической конференции «Современные информационные технологии». Пенза. Пензенская государственная технологическая академия. 2009.
Пономарев Д. Ю. О подходе к анализу сетей массового обслуживания с использованием тензорной методологии // Труды V Международной конференции «Идентификация систем и задачи управления» SICPRO '06. М. Институт проблем управления им. В. А. Трапезникова РАН. 2006.
Пономарев Д. Ю. Тензорный метод для телекоммуникационных сетей // Труды КГТУ. 2006. № 2–3.
Вишневский В. М. Теоретические основы проектирования компьютерных сетей. М. : Техносфера, 2003. 512 с.
Березко М. П., Вишневский В. М., Левнер Е. В., Федотов Е. В. Математические модели исследования маршрутизации в сетях передачи данных // Информационные процессы. 2001. Т. 1. № 2. С. 103–125.
Вержбицкий В. М. Основы численных методов : учеб. М. : Директ-Медиа, 2013. 847 с.
Линник Ю. В. Метод наименьших квадратов и основы теории обработки наблюдений. М. : Гос. издание физико-математической литературы, 1962. 352 с.

Еще

Статья