Применение линии тренда в MS Excel для прогнозирования квартплаты

Перед людьми часто встает вопрос о том, какую квартплату они будет платить в следующем году, а также как и, особенно, на сколько и почему увеличиваются отдельные виды платежей. В данной статье будет рассмотрен вопрос выявления зависимостей, которые позволят любому налогоплательщику легко рассчитать свою квартплату даже на ручном калькуляторе. Ввиду того, что квартплата зависит от типа дома, площади квартиры и количества проживающих, мы произвели расчеты квартплаты применительно к двухкомнатной квартире панельного пятиэтажного дома в Санкт-Петербурге с одним проживающим.

Для начала посмотрим, как изменилась оплата различных видов коммунальных услуг с января 2001 г. по де- кабрь 2008 г. включительно, значения которых представлены в табл. 1 по степени их уменьшения. Из таблицы видно, что первые места по увеличению платежей занимают: вывоз мусора, содержание и текущий ремонт общественного имущества дома и итоговая квартплата соответственно, которые повысились в 6 – 8 раз. Меньше всего изменилась оплата за содержание придомовой территории и за холодную воду. Здесь следует сразу оговорится, что в статье не рассматривается такой платеж как “текущий ремонт общего имущества многоквартирного дома”, который составляет на сегодняшний день 205 руб., т.к. данный платеж в счете-квитанции появился только с августа 2005 г. и для проведения статистического анализа имеет еще мало значений [3].

Таблица 1. Изменение отплаты за рассматриваемый период времени

№ п/п	Вид платежа (переменные)	Январь 2001, руб.	Декабрь 2008, руб.	Отношение 2008/2001
1.	вывоз мусора	11,05	88,45	8,005
2.	содержание общественного имущества многоквартирного дома	22,9	152,21	6,647
3.	итоговая квартплата	248,81	1456,52	5,85
4.	уборка лестничных клеток	10,78	57,02	5,289
5.	горячее водоснабжение	41,48	175,5	4,231
6.	отопление	115,39	487,61	4,226
7.	газоснабжение	5,5	22,15	4,027
8.	холодное водоснабжение и водоотведение	47,61	158,23	3,323
9.	содержание придомовой территории	32,78	57,92	1,767

На следующем этапе были получены полиноминальные зависимости изменения итоговой квартплаты, а также платежей за холодную и горячую воду и отопление, на которые приходится половина квартплаты (50,12%). В начале был проведен корреляционно-регрессионный анализ и получены коэффициенты корреляции R2 переменных, представленных в табл. 1 по 96 точкам, т.е. с января 2001 по декабрь 2008 гг. (см. табл. 2). В качестве примера полученной полиноминальной зависимости можно привести представ- ленную ниже формулу (1) для расчета итоговой квартплаты (рис. 1) С.

С = - 2 E - 08 x ⁶ + 6 E - 06 x ⁵ - 0 , 0007 x ⁴ + ... ... + 0 , 0357 x ³ - 0 , 7225 x ² + 13 , 943 x + ...

... + 229 , 96 .                                   ( 1 )

Здесь под величиной х имеются ввиду точки месяцев. Так, например, х = 97 будет характеризовать январь месяц 2009 г., а х = 98 февраль 2009 г. и т.д.

Рост итоговой квартплаты, руб.

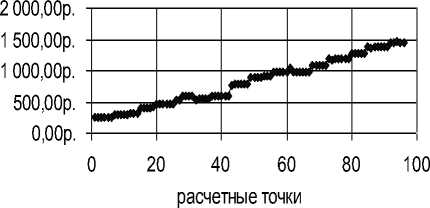
Рисунок 1. Рост итоговой квартплаты с января 2001 по декабрь 2008

Для проведения анализа и получение формулы 1 использовалась встроенная в MS Excel функция “Линия тренда” [1, 2, 3].

Но, несмотря на то, что для выведенной формулы 1 был выявлен достаточно высокий коэффициент корреляции для неё R ² = 0,9902, полученная зависимость дала плохой результат при прогнозировании табл. 2, а в ряде случаев для других видов оплат даже отрицательное значение при степени n = 6. Это относилось и к другим видам платежей, представленных в табл. 1. Основная причина этому кроется в том, что изменения величин оплаты обычно происходит один раз в год скачкообразно и в последние годы в основном в августе месяце, в то время как в 2001 по 2005 гг. увеличение итоговой квартплаты иногда происходило даже по несколько раз в год. Поэтому был произведен статистический анализ по двум месяцам в году - январю и декабрю. Ниже представлены таблицы 2 - 5, которые наглядно показывают, как изменяется расчетная оплата за холодную и горячую воду и другие виды коммунальных платежей в зависимости от степени n применяемой полиноминальной зависимости, а также показан процент отличия расчетной величины от реальной их оплаты и величина процента, на которую отличается реальная оплата, принятая за 100%, к расчетной оплате.

Таблица 2. Прогноз стоимости холодной воды на январь 2009 г.

степень полинома n	6	5	4	3	2
расчетная оплата, руб.	164,81	172,60	229,94	179,24	197,10
коэффициент корреляции R 2	0,9985	0,9979	0,9979	0.9978	0,9974
оплата на январь 2009 г., руб.	199,86
% отличия расчетной величины от реальной оплаты	115,89	87,31	92,86	94,68	92,68
разница %	+15,89	-12,69	-7,14	-5,32	-7,32

Как видно из расчетов, несмотря на большую величину коэффициента корреляции R ² = 0,9985 при n = 6, результаты расчета показали большое отклонение от реальной цены на холодную воду, которое равно -31,75 (164,81 - 199,86 = -31,75). Самый же лучший результат расчета был получен для n = 3, т.к. имеет самый меньший процент отличия расчетной величины от реальной оплаты. Аналогичные выводы были получены для горячей воды и отопления, но только при значениях величины степени n = 4 (см. табл. 3 и 4). Из таблиц также видно, что разница между реальными платежами и расчетными составила всего 5-7%.

Теперь рассмотрим расчет итоговую квартплату на январь 2009 г., представленной в табл. 5, из которой видно, что при степени n = 4 (формула 2) мы получили самое лучшее значение, отличающее от реальной оплаты всего на 1,3%.

С = 0 , 7283 x ⁴ - 13 , 938 x ³ + 92 , 48 x ² - ...

... - 78 , 32 x + 317 , 55 . ( 2 )

Здесь под величиной х имеются ввиду годы, например, х = 2009 будет характеризовать январь месяц 2009 г.

Таким образом, можно сделать следующие выводы:

• •    несмотря на то, что коэффициенты корреляции R ² были самыми высокими при степени полиноминальной зави-

• Э.А. Пиль

симости n = 6, использование полученных формул не рекомендуется, т.к. они показывают большие отклонения результатов при прогнозировании в сравнении с реальной оплатой и, кроме того, иногда даже имеют отрицательные значения;

• •    при расчетах основных видов платежей квартплаты следует использовать полиноминальные зависимости со степенью n = 3 и n = 4;

• •    при расчете итоговой оплаты необходимо применять полиноминальную зависимость со степенью n = 4.

Следующая табл. 6 и построенный на ее основе рис. 2 показывает, как изменялась итоговая квартплата в процентом отношении к предыдущему году. Из табл. 6 видно, что итоговая квартплата дважды резко поднималась в 2002 и 2004 гг. на 47,68 и 41,06% соответственно, что значительно выше установленной инфляции в эти годы. Далее, начиная с 2005 г., идут небольшие ее скачкообразные изменения. То есть, в последние три года увеличение итоговой квартплаты приблизительно соответствовало в среднем величине официальной инфляции в стране. Теперь проведем прогноз с помощью повышения итоговой квартплаты на основе табл. 6. Для этого рассчитаем среднее значение процента увеличения итоговой квартплаты за последние 3 года Сср = (110,84+117,64+114,14)/3 = 114,21. После этого умножив итоговую квартплату за 2008 г. на Сср получим величину прогнозируемой квартплаты на январь 2009 г. Скв = Сср 1456,5 = 1663,46 руб. Полученная расчетная величина также очень хорошо согласуется с реальной и отличается всего на 0,71%, что почти в 2 раза точнее, чем проведенные расчеты по выведенной полиноминальной зависимости при n = 4, представленной в табл. 5, где эта величина составляет 1,3%.

Таблица 3. Прогноз стоимости горячей воды на январь 2009 г.

степень полинома n	6	5	4	3	2
расчетная оплата, руб.	231,61	174,50	185,04	189,20	185,23
коэффициент корреляции R 2	1,0	1,0	0,998	0,9888	0,9845
оплата на январь 2009 г., руб.	199,86
% отличия расчетной величины от реальной оплаты	75,71	79,29	105,63	82,34	90,54
разница %	-24,29	-20,71	+5,63	-17,64	-9,46

Таблица 4. Прогноз стоимости отопления на январь 2009 г.

степень полинома n	6	5	4	3	2
расчетная оплата, руб.	430,34	487,35	639,80	498,22	547,64
коэффициент корреляции R 2	1.0	1.0	0,998	0,9888	0,9845
оплата на январь 2009 г., руб.	596,72
% отличия расчетной величины от реальной оплаты	72,96	81,67	107,22	83,49	91,78
разница %	-27,04	-18,33	+7,22	-16,51	-8,22

Таблица 5. Прогноз итоговой квартплаты на январь 2009 г.

степень полинома n	6	5	4	3	2
расчетная оплата, руб.	430,34	1934,15	1719,16	1597,65	1638,75
коэффициент корреляции R 2	0,9965	0,9953	0,9947	0,9939	0,9917
оплата на январь 2009 г., руб.	1651,81
% отличия расчетной величины от реальной оплаты	90,6	114,39	98,7	91,17	97,43
разница %	-9,4	+14,39	-1,3	-8,83	-2,57

Таблица 6. Процентное увеличение итоговой квартплаты последующего года к предыдущему

год	2001	2002	2003	2004	2005	2006	2007	2008
квартплата, руб.	311,5	460,01	557,88	786,97	978,62	1084,72	1276,1	1456,5
%	-	147,68	121,28	141,06	124,35	110,84	117,64	114,14

Основываясь на полученных выше      предполагаемую оплату итоговой кварт- выводах теперь можно спрогнозировать      платы на август - декабрь 2009 г. которые представлены в табл. 7, на основе полученных полиноминальных зависимостей,. Исходя из сделанного выше вывода, что для расчета итоговой квартплаты рекомендуется использовать полиноминальную зависимость n = 4 и ввиду того, что обычно квартплату изменяют в августе месяце, она, вероятно, составит 1719,16 руб.

процентное увеличение итоговой квартплаты по отношению к предыдущему году

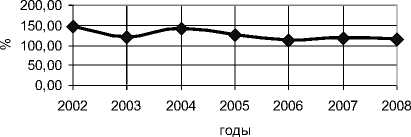
Рисунок 2. Процентное увеличение итоговой квартплаты по отношению к предыдущему году

Это можно также видеть и из полученных цифр. Так, например, квартплата не может быть меньше, чем в предыдущем году. То есть расчетные цифры 430,34 руб., 1597,65 руб. и 1638,75 руб. отпадают сразу. Величина оплаты в 1934,15 руб. явно завышена. Поэтому по логике величина итоговой квартплаты в 1719,16 руб. является более достоверной. Здесь сразу следует оговориться, что эти расчеты будут реальными, конечно, при условии, что не произойдет форсмажорных обстоятельств и квартплату не заморозят указом правительства ввиду продолжающего экономического кризиса и отсутствия у уволенных граждан денег на оплату коммунальных услуг.

В завершении рассмотрим, как изменялась в процентном отношении годовая итоговая квартплата по отношению к годовой зарплате автора (см. табл. 8).

Таблица 7. Прогнозируемая итоговая квартплата на август-декабрь 2009 г.

степень полинома n	6	5	4	3	2
расчетная оплата, руб.	430,34	1934,15	1719,16	1597,65	1638,75
коэффициент корреляции R 2	1.0	0,997	0,9965	0,9957	0,9953

Таблица 8. Процентное отношение годовой итоговой квартплаты к годовой зарпла те.

год	2004	2005	2006	2007	2008
процентное  отношение  годовой  итоговой квартплаты к годовой зарплате	5,55	4,02	5,06	5,6	5,79

Построенная табл. 8 дает наглядное представление, что в процентном от- ношении итоговая квартплата в последние годы растет быстрее, чем зарплата, хотя качество предоставляемых услуг ЖКХ оставляет желать лучшего.

Исходя из всего вышесказанного можно сделать общие выводы: 1) полученные полиноминальные зависимости как для отдельных видов платежей, так и для итоговой квартплаты можно спрогнозировать на достаточно высоком уровне; 2) эти зависимости можно распространить и на другие виды домов только с поправкой соответствующих коэффициентов.

Полученные зависимости и выводы можно распространить и на другие типы домов и квартир.