Применение Maple для моделирования динамического состояния RLC-цепи при импульсном воздействии на термистор

В настоящее время теоретические положения и практические методы математического и компьютерного моделирования применяются во многих предметных областях, например, электродинамика. Необходимо также отметить, что развитие методов и средств математического и компьютерного моделирования позволяет сделать процесс решения задач из вышеназванной предметной области более эффективным. Поэтому обучение владением методами и инструментарием компьютерного моделирования является крайне важным. Широко используемый инструментарий, применяемый в компьютерном моделировании, это такие программные системы как MATLAB, Maple и др. [1-4]. С их помощью решают различные проблемы [48].

В данной работе рассмотрена электрическая система являющаяся последовательной RLC-цепью. Система находится в режиме установившихся колебаний. В некоторый момент времени происходит импульсное воздействие на термистор, например, нагрев при помощи достаточно мощного лазерного излучения. В результате происходит резкое изменение сопротивления, после чего начинаются переходные процессы. Представленные результаты моделирования показывают динамическую картину изменения состояния электрической системы.

Постановка задачи . Пусть имеется последовательная RLC-цепь, в которой содержатся источник ЭДС, термистор R, индуктивность L и емкость С (рис. 1).

Будем предполагать, что сопротивление термистора представляет из себя дискретно – континуальную характеристику, т.е. может скачкообразно меняться под внешним воздействием.

В качестве искомой величины будем брать силу тока i(t). Тогда в случае установившегося режима колебаний в RLC-контуре, уравнение, соответствующее данному случаю, можно записать в следующем виде [1]:

L --^у i ( t ) + R • — i ( t ) + — • i ( t ) = —E ( t ) dt ^{2 (} ) dt ⁽ ) C ⁽ ) dt ⁽ )

, где E(t) - электродвижущая сила: E(t) A-sin(ro-t);

A – амплитуда в вольтах (В);

го - круговая частота (рад/с);

t – время в секундах (с).

В случае, когда в некоторый момент времени t0 происходит импульсное воздействие на термистор, уравнение (1) преобразуется в следующий вид:

L • ^-i ( t ) + ( R + 5 ( t ₀) • r ) • — i ( t ) + —• i ( t ) = —E ( t ) dt ^{2               0}       dt       C        dt

, где δ(t) – дельта функция Дирака.

Целью моделирования является получение информации о динамике поведения функции тока i(t) при импульсном воздействие на термистор.

Для большей наглядности изменение функции тока i(t) представляется в графическом виде.

Поиск решения

Для компьютерного моделирования зададим конкретные значения для параметров, входящих в математические модели (1) и (2):

L=0,4 Гн; R=20 ом; r=30 ом; C=0.02 Ф; го =15 рад/с; A=10 В; t0=15 с.

Для поиска аналитических решений (1) и (2) воспользуемся Maple [1-4]. Исходный текст на Maple для поиска решения (1) может выглядеть следующим образом:

> ^restort

>^L :=О.4:С,:=2.1О-²:Л_о:=1О:^     ^=30.0:

t_n — 15.0 : co •= 15 : R, — R_n + Dirac(lA -77.: >

> E= z^-sin(«>.,): ,_a:=,(0)-0,D(,)(0)-l:

^Дифференциальное уравнение в общем виде для тока в > установившемся режиме common my ode :=

L^WO) + 7? — (/(0) +77-00 dr          d t        ^c

= —(£(0) d t

> common_my_ode — L

,2                ( d       \

-^7 00 + 400 + d72      J I d?      )

d

d7

ко

= A G)cos(cof)

^Дифференциальное уравнение для конкретных значений параметров для тока в установившемся режиме myodeil_0 := subs^ J А = AQ, R = Ro, L = Lo, С = C^, co = 0)()

>

common my_ode^

my ode i l_0 == 0.4 —— /(0 + 20 — /(0 + 50 7(7) d7^{2              dz}

= 150 cos( 15 7)

# Решение дифференциального уравнения при конкретных

• >       ,е „„х  - токи в »=„,«„<,<—=,режиме

ту_i_l О init condition := rhs{dsolve{ {my ode i l О, zes}))

• >    # Решение „ри „динных ночаиькыхусоеиях

  f 15 _ 2167/J

  [ 458      45800 J

  
  

my_i_l_0_imt_c — е⁵ * ^{5 +} - 7s )'

, -5 (5 + 2 ТД t ( 15     2167 /У 'i _ 15 cos( 15 7)

• ⁶             ( 458      45800 )        229

225 sin( 15 7)

i i ( t ) = e

>

Таким образом, установившееся решение для (1) имеет вид:

5 ( -5+27 ) t  15   2167V5

^™

(458  45800 J

+ e

-5(5+27 ) t ( 15

■ (   ) — +

2167^ ) 15cos ( 15 t )   225sin ( 15 t )

---X----/ +------- -----/

^“

(458   45800 J

.

Далее, чтобы найти решение (2), необходимо знание начальных условий. Их можно определить, например, при помощи следующего исходного текста:

• >    # Решение в заданный момент времени

• >    my_i_l_0_t0 := simpli^_Sub_S(t = t₀ my_iJ_0_init.condition^

my_i_l_0_t0 — -0.4809845602

• >    # Значение производной решения в заданный момент времени

7., -7- ( mv i 7 0 init condition ) ] |

0 d 7   ----- -           ))

dmy_i_l _0_t0 — szzz/jo/z^j^sMTzs^? = t₍ dmyiJOjO— 1.792926138

Далее, находим решение (2) для t ≥15 при помощи следующего исходного текста: >  ^Добавляем дельта-функцию в уравнение

>

= co_Q , 7 = 7,1., common_my_ode^

myodeil1 — 0.4   ₂ /(^) "*" (20 + 30.0 Dirac^))

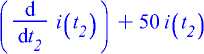
= 150cos(15 t_?^

> ics_l_l := /(0) = my_i_l_O_tOM^W=dmy_i_l_O_tO ics_l_l := /(0) = —0.4809845602, D(Z) (0) = 1.792926138

> Tny_l_l_l_init_condition := rhs^olve^my.odeJJJJcsJJ^J^y rnethod-laplace my J_1 _1 _init_condition -

1056000cos(Z7)9

+      229

245 760 cos(z?)15

432000 cos(z2)?

921600 cos(f7)13 229

90720cos^2)5

1382400 cos(f7)n

8400cos^)3

225 cos(/7)

+    229

-25t e 2 (34449062941693/Jsinh( 10 Z7/J) + 4757273214290cosh( 10 Л,л/5~)) 11450000000000

+ ^ (225 sin^7) ( (16 cos^7^4 — 16 cos^7^2 + 1)" — (8 cos(Z7)3

— 8cos(z7j) ^ ( (4cos(z7)2 — 1) — 4cos^2)2) (4cos(/7)2 — 1)} my_i_1 _0_init-Condition

my_solve :=

>

subset-, = t — tQ, my_i_l_1 _init-Condition^ t > tQ

Таким образом, решение для (2) при t ≥15 имеет вид:

i2(t)--

245760 cos ( t - 15 ) ¹⁵  921600 cos ( t - 15 ) ¹³

—

1382400cos ( t - 15 ) 11 229

1056000cos ( t - 15 ) 9   432000cos ( t - 15 ) ⁷  90720cos ( t - 15 ) 5   8400cos ( t - 15 ) 3

229               229              229             229

225cos ( t - 15 )

e -25 t ₊ ³⁷⁵ ( 34449062941693^5sinh ( 10 ( t - 15 ) 45 ) + 4757273214290cosh ( 10 ( t - 15 ) V5 ) ) 11450000000000                               ⁺

225sin ( t - 15 ) [ ( 16cos ( t - 15 ) 4 - 16cos ( t - 15 ) 2 + 1 ) 2 j +--- 458

( 8cos ( t - 15 ) ³ - 8cos ( t - 15 ) ) ^ ( 4cos ( t - 15 ) 2 - 1 ) - 4cos ( t - 15 ) 2 j ( 4cos ( t - 15 ) 2 - 1 ) 458

Таким образом, окончательный вид решения для (2) можно записать следующим обра- зом:

i (t )-

i1 (t)

i2 (t)

t <  15

t >  15

Результаты моделирования в графическом виде

Для представления полученного результата в графическом виде необходимо добавить, например, следующий исходный код на Maple:

plot^my solved = 10..^ + 3-t₀,labelfont = [18, 18],/яЛе/5 = [ 't','i(t)'], title

= typeset^ "График решения уравнения\п",5и/>»^₇ = t,my_ode_i_l_1^ ))

График решения уравнения

>

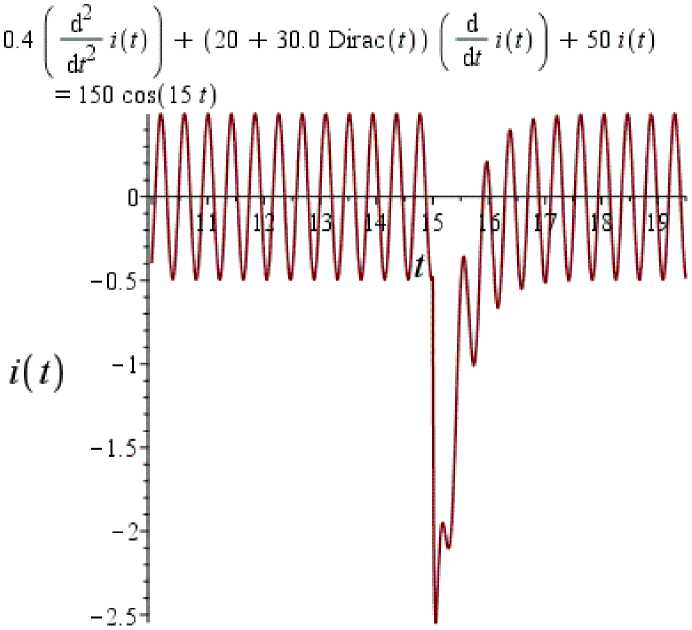
На графике видна реакция системы при импульсном воздействии на термистор во время равное t0=15 с. Увеличение тока почти в 5 раз. Время переходного процесса примерно 1.8 с.

Заключение. В статье был продемонстрирован подход, который можно применять во время обучения методам и инструментарию компьютерного моделирования. Результат дает представление о тре-

бованиях, предъявляемых к элементам электронных систем. В данном случае, для сохранения работоспособности, необходимо чтобы элементы цепи выдерживали краткосрочную нагрузку как минимум 2,5 А. Продемонстрированный исходный код достаточно легко модифицируем. Это способствует в процессе обучения хорошему закреплению обучающимися предлагаемого материала.