Применение марковских процессов при техническом обслуживании и ремонте летательных аппаратов с учетом критерия коррозионной стойкости

Сложные технические системы могут быть классифицированы в виде трех состояний:

• 1)    новая конструкция – обозначим это состояние как 0;

• 2)    зачищенная от коррозии конструкция – это состояние 1;

• 3)    замененная конструкция – обозначим как 2.

Не все указанные здесь состояния связаны с переходом друг в друга. Совершенно очевидно, что зачищенная конструкция уже не может возвратиться в состояние «новая». Зачистка производится в местах видимой коррозии, но остается еще много мест, где коррозия не видима, но уже имеет место [1].

Невозможен переход из состояния 2 в состояние 0. Это связано с тем, что замена обшивки сопровождается заменой конструктивных элементов. Кроме того, обшивка панели может быть заменена не целиком, а только частично, в местах обнаруженных коррозионных поражений.

Таким образом, схема переходов из одного состояния в другое, в общем случае, представлена на рис. 1.

Рис. 1. Схема переходов

При подсчете вероятностей переходов было учтено, что конструкция может переходить из состояния 1 в состояние 1, т. е. оставаться в состоянии 1, если производится повторная зачистка, а может переходить из состояния 2 в состояние 2, если повторная замена производится без фиксации состояния 1.

Соответственно имеет место следующая матрица переходов и переходных вероятностей (указаны в скобках):

Было Стало	0	1	2
0	00 ( Р 00 )	01 ( Р 01 )	02 ( Р 02 )
1	10 ( Р 10 )	11 ( Р 11 )	12 ( Р 12 )
2	20 ( Р 20 )	21 ( Р 21 )	22 ( Р 22 )

Вероятность перехода Р 00 означает вероятность того, что на предыдущем ремонте конструкция находилась в состоянии «новая» и при поступлении в очередной ремонт она также не нуждается в зачистке или замене.

Вероятность перехода Р 01 означает вероятность того, что на предыдущем ремонте конструкция наводилась в состояние «новая», а на следующем ремонте требует зачистки. Вероятность Р ₀₂ означает вероятность того, что на предыдущем ремонте конструкция находилась в состоянии «новая» и требует замены на следующем ремонте (без промежуточной зачистки).

Вероятность Р 11 означает вероятность того, что на предыдущем ремонте конструкция была зачищена и при поступлении в очередной ремонт вновь требует зачистки.

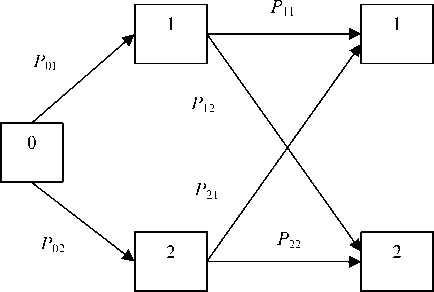
Рис. 2. Иллюстрация схемы переходов из одного состояния в другое

Аналогично: Р 12 – означает вероятность перехода из состояния 1 в состояние 2; Р 21 – вероятность перепада из состояния 2 в состояние 1 и Р 22 – вероятность перехода из состояния 2 в состояние 2.

Указанные матрицы представляли бы однородную цепь Маркова, если бы переходные вероятности Р ij зависели только от предыдущего состояния. При этом исчисления наработки панели надо было бы вести от предыдущего состояния к последующему. Пусть, например, наработка с начала эксплуатации при состоянии 2 есть Т ₂, и состояние 2 перешло в состояние 1. Пусть наработка с начала эксплуатации в состоянии 1 есть T 21 , тогда наработка при переходе 2–1 составит

( T 2i — Т ₂). Такой подход был бы правильным, если замена или зачистка полностью охватывала бы рассматриваемую зону, или если бы при дальнейшей дефектации координаты коррозии жестко фиксировались и лежали в области замены или зачистки.

На самом деле это не так. Зачистка выполняется лишь в местах появления коррозии и остается еще много площадок с необнаруженной коррозией. При дальнейшей дефектации коррозия может быть обнаружена вне зоны зачистки и нет возможности строго зафиксировать ее координаты, сказанное относится и к процессу замены (состояние 2). Это означает, что, например, переход 2-1 зависит не только от предыдущего состояния 2, но и от наработки самолета с начала эксплуатации. Здесь надо добавить, что не-обнаружение коррозии не означает ее полного отсутствия, а длительность эксплуатации оказывает существенное влияние на зачаточные коррозионные повреждения.

Сведение немарковских параметров системы к марковским. С теоретической точки зрения любой случайный процесс можно представить как процесс Маркова: для этого достаточно в понятие «состояние» включить всю предысторию поведения системы. Следовательно, о возможности аппроксимации Маркова необходимо судить с 2-х позиций: насколько точно модели Маркова отражают реальный характер случайных процессов и насколько сложны сами модели. Аппроксимация Маркова возможна, если потоки возникновения и устранения отказов и неисправностей являются простейшими, т. е. удовлетворяются условия ординарности и стационарности. Для определения вероятностей состояний P i возможна замена реальных функций распределения F i ( t ), характеризующих потоки, переводящие системы ЛА из одного состояния в другое, на экспоненциальные при условии равенства их первых моментов [2]. В некоторых случаях, вместо замены реальных законов распределения экспоненциальными путем приравнивания их математических ожиданий, можно использовать способ введения фиктивных состояний и представлений исследуемых процессов как кусочно-однородных. Зная характер изменения интенсивности потоков отказов, можно для каждого периода принять их постоянными to _1s ю ₂ и ю ₃ (что соответствует замене монотонно изменяющихся функций ступенчатыми) и решить ряд независимых задач для каждого периода. Но в этом случае возникает необходимость нахождения значений ю_ь ю ₂, ю ₃ и длительности периодов Т ₁ и Т 3 по имеющимся статистическим данным. В соответствии со сказанным, вероятность перехода Р у следует рассматривать как функцию Р у ( Т) от наработки Т с начала эксплуатации.

Фактически речь идет об условной вероятности переходов, при условии, что известна наработка с начала эксплуатации. В нашем случае производится замена вероятностных переходов Р ₀₁ и Р ₁₂( Р ₂₁) на кусочно-однородные процессы: Р ₀₁ - необслуживаемая нерезервируемая система, Р ₁₂( Р ₂₁) - как непрерывно контролируемая нерезервируемая система [3].

Модель состояний необслуживаемых нерезервированных конструктивных элементов (КЭ) летательных аппаратов (ЛА). Для необслуживаемых нерезервированных КЭ ЛА характерными состояниями являются: 1 - готовность к работе (Г); 2 - отказа (О).

В связи с невозможностью выявления и устранения возникших в процессе эксплуатации отказов будет иметь место лишь одно направление перехода: из состояния 1 в состояние 2 (1-2). Ориентированный граф состояний таких КЭ представлен на рис. 3.

Состояние 2 является поглощающим, и поведение этих КЭ описывается следующей системой дифференциальных уравнений:

dP₁( t ) dt

= ^- a 12 P ⁽ t )

dP ₂ ( t ) dt

= a 12 P ⁽ t )-

Интенсивность перехода a ₁₂ по своей физической сущности представляет собой интенсивность отказов X необслуживаемого КЭ:

a 12 = X .

Используя преобразование Лапласа, от системы дифференциальных уравнений (2) перейдем к системе алгебраических уравнений:

SP 1 ( S ) - P 1 (0) = - X Р 1 ( S );

SP 2 ( S ) - P 2 (0) = X P 1 ( S ).

Из данной системы найдем выражение для P ₁( S ):

P 1 ( S ) =

P 1 (0)

S + X .

Перейдя к оригиналу, окончательно получим

P 1 ( t ) = P 1 (0) e "^X t .                   (3)

1                                                  2

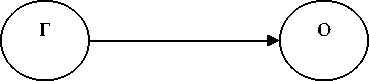
Рис. 3. График состояний необслуживаемых нерезервированных КЭ ЛА

В модели необслуживаемых КЭ (рис. 3) переменной является интенсивность отказов X . Значение вероятности P ₁(0) принимается равным оценке, полученной теоретическим путем или при заводских испытаниях. Характер изменения вероятности P ₁ застать КЭ в состоянии готовности к работе показан на графиках (рис. 4), построенных по исходным данным, приведенным в табл. 1 (значение P ₁(0) принято равным единице, что, как правило, имеет место при теоретических расчетах и является явно завышенной оценкой).

Из этих графиков видно, что даже при малых, трудно достижимых значениях X = 10-6 1/ч вероятность P1 готовности необслуживаемого КЭ к работе уже после одного года эксплуатации снижается до недопустимо малых значений (Р1(Т = 8 760 л. ч.) = = 0,9913). Это указывает на необходимость тщательной обработки статистических данных для оценки по результатам испытаний необслуживаемых КЭ с целью подтверждения правильности принятого главным конструктором решения о его необслуживаемости в процессе эксплуатации.

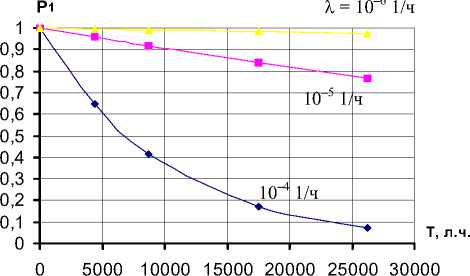
Рис. 4. Зависимость вероятности P ₁ , перехода Р (₀₁) от времени эксплуатации

Таблица 1

Вероятность P ₁ нахождения КЭ в состоянии готовности к применению

X , 1/ч	Т , л. ч.
	4 380	8760	17 520	26279
10-4	0,6453	0,4164	0,1734	0,072
10-5	0,9571	0,9161	0,8393	0,7689
10-6	0,9956	0,9913	0,9826	0,9741

Модель состояний непрерывно контролируемых нерезервированных конструктивных элементов летательных аппаратов. Для непрерывно контролируемых в процессе эксплуатации нерезервированных КЭ ЛА модель системы ТО имеет простейший вид (рис. 5). В любой произвольный момент времени такие КЭ могут находиться в одном из двух состояний: 1 - готовности к работе (Г); 2 - отказа (О).

Наличие непрерывного контроля технического состояния КЭ позволяет в случае возникновения отказа (переход 1-2) немедленно приступить к восстановлению его готовности (переход 2-1).

Рис. 5. График состояний непрерывно контролируемых нерезервированных КЭ ЛА

Система дифференциальных уравнений для представленной на рис. 5 модели будет иметь следующий вид:

dP i ^t)- = — a i2 ^p i ( t ) + a 2i ^p 2 ( t );            (4)

dt

• ^{2 (} t ) = - a P, ( t ) + a P, ( t ). 212     121

dt

Используя преобразование Лапласа, перейдем от системы дифференциальных уравнений (4) к системе алгебраических уравнений, что позволит получить выражение для вероятности P ₁( t ) нахождения КЭ в состоянии 1 готовности к работе (при начальном условии P ₁(0) = 1):

P ( t ) =

a 21

a 12 ⁺ a 21

+    a12     . e-(a12 + a21) t = a12 + a 21

^Ц + ™ нп . e ^- ( ™ нп ^{+ ц )} t ϖ _нп +µ ϖ _нп +µ

где а ₁₂ = ет _нп; а ₂₁ = 1/ Т ^нп_устр = ц ; ет _нп - параметр потока отказов непрерывно контролируемых нерезервированных КЭ; Т ^нп_устр - среднее время устранения отказов; ц - интенсивность восстановления.

В стационарном режиме эксплуатации ( t ^ » ) система уравнений (4) вырождается в систему алгебраических уравнений

• ^- a 12 ^P 1 ⁺ a 21 ^P 2 = ^{0; (6)} а 12 ^Р 1 ^- а 21 ^Р 2 = ⁰,

из которой с учетом нормировочного условия P ₁ + Р ₂ = 1 получаем

Р 1 =—^. (17) ^ϖ нп ^+µ

Выражения (5) и (7) широко известны из литературы по теории надежности и эксплуатации [4]. Но при этом модели Маркова позволяют получить еще целый ряд показателей качества систем ТО ( F i , p ij , ц i и др.).

В модели непрерывно контролируемых нерезервированных КЭ и систем ЛА вектор эксплуатационных характеристик х включает две характеристики: ю _нп и Т *^п_устр (или ц ). Графики изменения вероятности P ₁ готовности КЭ к работе приведены на рис. 6, они построены по исходным данным табл. 2. Из них видно, что при ю _нп <  10^-5 1/ч вероятность P ₁ практически не зависит от времени устранения отказов в реальном диапазоне их изменения [5].

Таблица 2

Вероятность P1 нахождения КЭ в состоянии готовности к применению

Т нпустр , ч	® , l/ч
	10-3	10-4	10-5
10	0,9901	0,9990	0,9999
25	0,9756	0,9975	0,9998
50	0,9524	0,9950	0,9995
100	0,9091	0,9901	0,9990

Так, при изменении Т“пустр на 90 % (с 10 до 100 ч) вероятность P1 изменяется всего лишь на 0,09 %. Однако при юнп > 10-5 1/ч картина меняется: изменение Тнпустр на 90 % при юнп = 10-4 1/ч приводит к изменению P1 на 0,9 %, а при юнп = 10-3 1/ч - на 8 %. Следовательно, в ходе проведения испытаний исходя из достигнутого уровня юнп требования к точности нахождения оценки времени Тнпустр и, следовательно, числу испытаний должны быть различны для значений ωнп ≤ 10–5 1/ч и ωнп ≥ 10–5 1/ч.

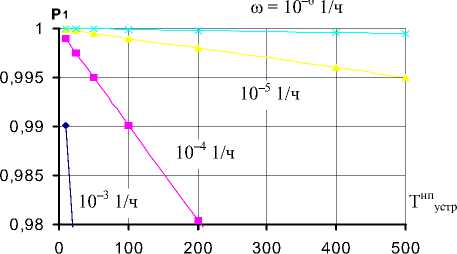
Рис. 6. Зависимость вероятности Р ₁ , перехода Р ₁₂ , от времени устранения отказов

Таким образом, создание матрицы вероятностей переходов из одного состояния в другое позволяет осуществлять прогнозирование развития коррозионных поражений и оценивать минимальный, средний, максимальный объем работ и расход материальных ресурсов, связанных с устранением коррозии при поступлении ЛА в ремонт.

Сведение немарковских параметров системы к Марковским и представление исследуемых процессов как кусочно-однородных позволило провести оценку вероятности P 1 нахождения систем панелей обшивки фюзеляжа в состоянии готовности к применению по назначенному техническому обслуживанию и определить вероятность работоспособности конструктивных элементов для самолетов типа Ан-24 .