Применение машинного обучения к планиметрическому анализу минералов как задаче классификации в различных постановках

Минералогический анализ по визуальным данным представляет собой недорогую и менее затратную по времени альтернативу сложным и дорогостоящим химическим или радиологическим методам анализа. Для определения удельного содержания некоторого минерала по визуальному изображению образца руды используется так называемый площадной анализ, суть которого заключается в оценке относительной площади минерального пятна, соответствующего интересующему нас компоненту (минералу), на плоском изображении образца и экстраполяции полученной площадной оценки на весь его объем. В свою очередь, одним из методов получения площадной оценки является планиметрический метод, в рамках которого на изображение накладывается прямоугольная, обычно квадратная, сетка и затем осуществляется отнесение каждой ячейки сетки к тому или иному компоненту руды.

Таким образом, планиметрический метод минералогического анализа можно рассматривать как задачу классификации, где в роли объектов выступают ячейки планиметрической сетки, а в роли классов — идентифицируемые минералы, присутствующие в образце руды. В «классическом» планиметрическом анализе идентификация объекта с классом осуществляется вручную экспертом-минералогом. Основная идея данной работы заключается в исследовании возможностей автоматизации этого процесса с помощью моделей машинного обучения (МО), которые используются в двух аспектах — для получения абстрактного векторного представления классифицируемого образца и для отнесения последнего к одному из заданных классов.

Мы рассматриваем три варианта постановок задачи автоматизированной идентификации ячеек планиметрической сетки с тем или иным классом: мягкая, бинарная и мультиклассовая классификация. Для каждого варианта предложены формальные постановки и проведены эксперименты по тренировке соответствующих нейросетевых классификаторов и проверке их эффективности при определении удельного содержания минерала в руде. Исследования проводились на примере апатитовых руд Хибинского месторождения различных видов. Задача минералогического анализа рассматривалась в упрощенном виде: определить удельное содержание апатита в образцах руды, представленных цифровыми изображениями. В этом прикладном аспекте задача свелась к бинарной классификации, где положительный класс представляет искомый минерал, а отрицательный класс — все прочие компоненты руды.

Специфической проблемой автоматизации планиметрического анализа является то, что в идеальном случае все ячейки планиметрической сетки должны принадлежать строго одному классу (включать в себя единственный минерал). Однако, на практике, очевидно, это недостижимо — при любом размере сетки наряду с «чистыми» представителями классов, среди ячеек будут присутствовать «пограничные» образцы, относящиеся к более, чем одному классу одновременно. Неизбежна ошибка дискретизации, связанная с тем, что реальные формы минеральных пятен аппроксимируются множеством прямоугольников. Уменьшение размера сетки снижает ошибку дискретизации, попутно снижая возможность учета морфологических и текстурных свойств минералов.

Нужен компромиссный размер сетки, сочетающий точное определения содержания минерала в образце с точной классификацией элементов. Строго говоря, планиметрический анализ является задачей мягкой классификации, когда степень принадлежности объектов классу может лежать в диапазоне от 0 до 1. Крайние значения степени принадлежности соответствуют ячейкам, целиком принадлежащим положительному или отрицательному классам, а промежуточные — ячейкам, лежащим на границе минерального пятна.

Ключом к успешному решению задачи классификации является выбор классифицирующих признаков. Для формирования вектора признаков, обеспечивающего эффективное разделение множества объектов на классы, мы использовали предобученный векторизатор изображений ResNet18, представляющий собой сверточную искусственную нейронную сеть (ИНС), выдающую на выходе 512-компонентый вектор, соответствующий входному изображению [1] . Предварительные эксперименты показали весьма хорошую разделимость рассматриваемых классов объектов в таком признаковом пространстве.

Основной вклад данной работы заключается в анализе различных постановок задач планиметрического анализа как задач классификации и в экспериментальной проверке эффективности их решения методами машинного обучения в применении к площадному анализу изображений, объекты которых обладают свойствами смежности и однородности классов. В частности, в работе адресуются следующие исследовательские вопросы:

• (1 )    Насколько эффективно использование классификационных признаков, полученных с помощью векторизатора изображений на основе предобученной сверточной ИНС, для идентификации минеральных пятен апатита на изображениях образцов руды в видимом спектре?

• (2 )    Каковы предельные размеры планиметрической сетки, обеспечивающие эффективное определение удельного содержания апатита по изображению образца руды?

• (3 )    Какие варианты постановки задачи классификации наиболее эффективны с точки зрения точности определения удельного содержания минерала в руде планиметрическим методом?

Оставшаяся часть статьи организована следующим образом: в первой части кратко рассмотрены задача площадного минералогического анализа и существующий опыт применения машинного обучения для ее решения, а также формальный анализ планиметрического анализа как задачи классификации в различных постановках. Во второй части представлены результаты экспериментов по применению планиметрического анализа в рассматриваемой постановке к определению удельного содержания полезного компонента в апатитовых рудах.

1.    Площадной минералогический анализ на базе машинного обучения

Площадной анализ образцов горной породы, впервые предложенный французским минералогом Делессе [2] , заключается в измерении площадей минеральных пятен на двумерных изображениях плоских сечений руд или препаратов, изготовленных из разрозненных частиц минералов. При этом, в соответствии с принципом Делессе, предполагается, что площадная оценка эквивалентна объемной. В проекции на задачи машинного зрения, можно, таким образом, выделить два этапа площадного анализа:

• (1 )    сегментация изображения,

• (2 )    идентификация сегментов с тем или иным минералом (классификация).

Также возможно совмещение этих двух этапов в рамках семантической сегментации на базе глубоких ИНС [3] . Рассматриваемый в данной работе планиметрический метод площадного анализа, когда изображение разбивается на равные части (ячейки планиметрической сетки) и объектом классификации является отдельно взятая ячейка, можно считать альтернативой методам, основанным на сегментации.

Для автоматизации минералогического анализа в настоящее время широко используется машинное обучение (МО). Вне зависимости от способа выделения идентифицируемых с минералом областей изображения, определяющее влияние на качество последующей классификации выделенных объектов оказывает выбор набора признаков, которые должны хорошо разделять объекты в соответствующем пространстве. Характерной особенностью ранних и некоторых современных работ в данной области является использование эвристик при формировании признаковых векторов объектов. К таким эвристикам относятся представления изображения в различных цветовых моделях, статистические характеристики изображения, съемка в различных диапазонах и др. Например, авторы [4, 5] используют различные эвристические признаки для выделения сегментов изображения и последующей их идентификации с тем или иным минералом с помощью различных моделей машинного обучения.

Эффективной альтернативой эвристическим подходам к формированию признаков являются предобученные сверточные ИНС, позволяющие выделять абстрактные векторы, наилучшим образом идентифицирующие рассматриваемые классы объектов [6] . Например, в [7] авторы используют сверточную ИНС Yolo для визуальной идентификации каменного угля на фоне пустой породы. В работе [8] с помощью глубокой ИНС авторы решают задачу идентификации образца с минералом из заданного ограниченного набора. В работе [9] авторы исследуют возможность применения различных нейросетевых классификаторов для идентификации коллекционных образцов руды, при этом в качестве векторизатора признаков также используются сверточные ИНС. Отметим, что в упомянутых работах рассматриваются образцы чистых минералов, без примесей, то есть непосредственно решается задача классификации образца, в качестве которого в данном случае выступает изображение целиком.

Одна из первых работ, посвященных минералогическому анализу на основе сегментации изображений, описана в [10] . В ней предложен алгоритм автоматической сегментации цветных изображений горных пород с использованием методов кластерного анализа (K-means) на основе цвето-яркостных признаков. В последующих работах этого исследовательского коллектива [11] к идентифицирующим признакам минералов были добавлены морфологические свойства элементов изображения — площадь и геометрические пропорции минерального пятна. В соответствии с предложенным авторами подходом, на начальном этапе осуществляется кластеризация объектов изображения по цвето-яркостным признакам, а затем с помощью алгоритмов компьютерной графики определяются морфологические признаки полученных кластеров.

В работе [9], наряду с чистыми образцами минералов, рассматриваются случаи, когда минерал представлен в образце породы отдельными вкраплениями. Применительно к таким случаям в работе предложен оригинальный алгоритм автоматической (zero-shot) сегментации изображения, основанный на GradCAM-методах [12, 13].

Привлекательной стороной методов, основанных на сегментации изображений, является их независимость от способа получения изображения: могут использоваться как обычная фотосъемка в различных световых диапазонах, так и микрофотосъемка или съемка с использованием сканирующих микроскопов. Различные условия съемки позволяют сформировать изображения с максимально контрастным разделением минералов.

Однако, сегментация изображений в применении к задаче площадного минералогического анализа сопряжена с рядом сложностей, к числу которых относятся высокая вариативность текстур и цветов минералов, зашумленность изображений и влияние освещения, сходство минеральных структур и их взаимное перекрытие. Всё это затрудняет создание универсальных алгоритмов сегментации, которые могут работать с разными типами минералов. Работы в направлении решения этой проблемы ведутся на протяжении многих лет, см., например [14 , 15] , однако кардинального решения пока не найдено.

Значительные успехи в решении задач минералогического анализа на базе машинного обучения связаны с появлением глубоких сверточных нейронных сетей, позволивших решать задачи семантической сегментации. В данном случае осуществляется не только выделение на изображении однородных областей, но и их одновременная идентификация с заданными классами. Однако, применение семантической сегментации на базе глубоких ИНС сопряжено с необходимостью в изображениях высокого качества и в большом объеме тренировочных данных. Это затрудняет получение универсальных недорогих решений, работоспособных на широком спектре различных минералов и не использующих дорогостоящие технические средства.

Например, в работе [16] для выделения минеральных пятен глины на изображениях пород из нефтегазовых месторождений использована свёрточная нейронная сеть U-Net [17]. Это обеспечило довольно высокую точность сегментации (около 92 %), однако при этом использовались изображения, полученные с помощью сканирующего электронного микроскопа (SEM), а эффективность подтверждена только на рассматриваемом минерале. В работе [18] исследована эффективность различных архитектур сверточных сетей в задаче семантической сегментации 2D и 3D изображений мульти-минеральных образцов. Результаты проведенных авторами экспериментов показали большую вариативность точности сегментации в зависимости от рассматриваемого минерала. В целом, авторы отмечают, что применение глубоких нейронных сетей обеспечивает достаточно высокую точность сегментации, но их обучение требует значительных ресурсов и размеченных данных высокого качества.

Таким образом, решение задачи площадного минералогического анализа по визуальным данным с использованием планиметрического метода с последующей классификацией ячеек планиметрической сетки представляется перспективной менее ресурсоемкой альтернативой подходам на основе сегментации.

В качестве объекта классификации в рассматриваемой задаче выступает ячейка планиметрической сетки (далее в данной статье именуемая также «секцией»). Задача заключается в отнесении каждого элемента множества объектов X = {x 1 ,... ,x n } к одному из классов из заданного множества C = {с 1 ,..., с к } . В контексте определения содержания полезного компонент а 1 в апатитовой руде нас интересует доля минерала «апатит» в общем объеме руды, поэтому, с точки зрения рассматриваемой прикладной задачи, классификация является бинарной — один класс (позитивный) составляют объекты, относящиеся к минеральным пятнам апатита, а второй (негативный) — все остальные объекты. Поскольку, как отмечалось ранее, ячейка сетки может быть пограничной и включать в себя разные минералы, при использовании планиметрического метода анализа мы имеем дело с задачей мягкой классификации, когда для каждого объекта должна быть определена степень принадлежности к классам из множества C

C i (x) е [0,1].

Одной из гипотез, рассматриваемых в работе, является то, что степень принадлежности к классу в данном случае можно интерпретировать как оценку содержания соответствующего минерала в образце. Тогда удельное содержание k-го минерала будет определяться по формуле

Е» c k (x i )

⁽¹⁾ p ⁽ c k )= i N— .

где N — общее количество объектов классификации (ячеек планиметрической сетки).

Рассматриваемую задачу определения полезного компонента в руде (задачу бинарной классификации) можно также интерпретировать как многоклассовую, если считать объекты со степенью принадлежности положительному классу, лежащей в некотором диапазоне [c min , c max ], самостоятельным i-м классом. При этом интервал степени принадлежности исходного положительного класса разбивается на K непересекающихся подинтервалов

KK

U [c min , c max ] = [о, 1],       q [c min , c max = 0 .

Иными словами, степень принадлежности рассматривается в данном случае как идентифицирующий признак класса. В этом случае удельное содержание искомого минерала (положительного класса) будет определяться по формуле

• (3)    P(c + ) = ,

где N i — количество идентифицированных объектов (ячеек) i-го класса; c i — содержание искомого минерала в ячейках i-го класса.

При такой интерпретации наряду с ошибкой классификации на точность влияет и ошибка дискретизации, возникающая из-за того, что объектам, принадлежащим промежуточным классам (со степенью принадлежности к апатиту ci(x) g]0,1[), будет приписываться некоторое усредненное содержание искомого минерала, в общем случае отличное от фактического. В предельном случае, когда все объекты класса расположены (по степени принадлежности к положительному классу) на одной из границ интервала [cmin, cmax], а в качестве ci выбрана противоположная min ci .

граница, эта ошибка будет равна c _i ^max

Особенностью рассматриваемой здесь задачи является то, что классы в нашем случае не являются произвольными независимыми множествами объектов, но упорядочены друг относительно друга по степени принадлежности их элементов исходному положительному классу. С учетом соотношения (2) , назовем это свойством смежности классов в пространстве идентифицирующих признаков. В таком случае между любой парой классов можно определить дистанцию в пространстве с, при этом

• c i — C j -----------> 1 = max .

i → K, j → 1

Эта особенность ограничивает возможность увеличения количества классов с целью уменьшения ошибки дискретизации, поскольку это ведет к возрастанию максимальной дистанции между классами в пространстве c, что негативно сказывается на точности определения содержания искомого минерала.

Обозначим через £ =1 — acc, где acc —доля правильных ответов (accuracy), общую ошибку мультиклассового классификатора, а через ξ i j — ошибку классификации объектов j -го класса в пользу i -го класса (доля объектов j -го класса, ошибочно классифицированных как объекты i -го класса). Если при тренировке классификатора не учитывается взаимное расположение классов в пространстве с, то ошибка классификации будет распределена равномерно по классам, то есть

• « K—1 V i = j,

где K — общее количество классов.

Тогда ошибка определения содержания полезного компонента (положительного класса) будет равна к t '

S S K - l N i\ c l - C i | i=1 l=i

• ⁶ =-------- N -------,

где N i — количество объектов, классифицированных как принадлежащих i -му классу, N — общее количество объектов.

Как видим, ошибка зависит от дистанции между классами в пространстве с, что обусловливает дополнительное требование к используемому классификатору на базе машинного обучения: при тренировке классификатора целесообразно использовать штрафную функцию, зависящую от дистанции между классами. Это позволит снизить вероятность ошибок классификатора в пользу классов, удаленных от заданного в пространстве с, и снизить, тем самым, ошибку определения содержания полезного компонента.

Ввиду упомянутой выше особенности задачи, оценку качества классификации в нашем случае целесообразно производить с использованием взвешенных усредненных оценок точности. Обозначим вес ошибки классификации объекта j -го класса в пользу объекта i -го класса как λ ij . С учетом того, что максимально возможная абсолютная ошибка определения удельного содержания полезного компонента (ПК) при ошибочном отнесении объекта к соседнему классу равна K , вес ошибки будет определяться по формуле

А = ^л ц

1 + \ i — j \

K

Тогда взвешенная оценка количества ложно-позитивных срабатываний для i-го класса будет равна

K

FPW = £ Xij FPij, j=i где F Pij — количество объектов j-го класса, ошибочно идентифицированных как объекты i-го класса.

В свою очередь, взвешенная усредненная оценка точности многоклассовой классификации (micro-averaging) будет определяться по формуле

P rec ^W

K

∑︁ TPi i=1

KK

£ TP + £ FP^

i=i

i=i

В контексте задачи классификации изображение апатита обладает однородностью по используемому классифицирующему признаку. Иначе говоря, фрагмент участка изображения, идентифицированного по используемому классифицирующему признаку с классом c k , будет принадлежать классу c k с той же степенью, что и исходный участок. Обозначим через x _i ^{d 0} объект классификации, полученный путем наложения на исходное изображение планиметрической сетки размером d o , а через x dj ¹ — разбиение исходного объекта путем наложения более мелкой сетки размером d 1 < d o , то есть и x dj = x d ⁰ .

j

Тогда свойство однородности объектов классификации может быть сформулировано следующим образом:

^xd0: ck (xd) ~1 ^ ck (xdj) ~ ck (xd0), где ck (x) — степень принадлежности объекта k-му классу.

Можно предположить, что существует некоторая нижняя граница размера секции, при которой условие (4) перестает выполняться и используемый для классификации набор признаков перестает давать хороший результат. В предельном случае размер секции может быть равен одному пикселю и тогда признаковый вектор вырождается до используемой цифровой модели изображения, по которой идентифицировать минерал по меньшей мере сложнее, если вообще возможно.

В отношении апатита этот факт подтверждается проведенными экспериментами. Таким образом, значение d, характеризующее размер сетки, является параметром алгоритма классификации.

2.    Экспериментальная оценка эффективности планиметрического анализа апатитовых руд с использованием машинного обучения

Для экспериментов использовались пять изображений апатитовой руды Хибинского месторождения различных видов с разной концентраци ей полезного компонента и соответствующие им изображения-маски, на которых области, соответствующие апатиту, закрашены в черный цвет, а фон— в белый (таблица 1) . Разрешение исходных фото-изображений составляет 300 dpi, размер —915 x 709 пикселей, изображения получены обычной фотокамерой. Изображения-маски формировались путем ручной разметки экспертами-минералогами.

Таблица 1. Образцы изображений апатитовой руды, использованные в экспериментах

Вид руды	Апатитовый уртит	Пятнисто-полосчатая	Пятнистая	Линзовидно-по лосчатая	- Блоковая
Индекс образца	a	b	c	d	e
Фото	Я			^^^^
Маска			Яй		^Й. X
Содержание ПК	25%	41%	50%	40%	25%

Для получения набора объектов, используемых в дальнейших экспериментах, на изображения образцов руды и соответствующие им маски накладывалась планиметрическая сетка различных размеров, после чего для каждого объекта рассчитывался показатель фактического содержания полезного компонента как доля черных пикселей в соответствующем изображении-маске в общем числе пикселей изображения. С целью увеличения размера датасетов, в дальнейших экспериментах применялись приемы аугментации — многократное наложение планиметрической сетки со смещением, а также поворот изображений.

Эталонным набором признаков, однозначно идентифицирующих минерал, по определению, является его химический состав. Очевидно, что химический состав не может быть напрямую определен по изображению образца, поэтому для визуального минералогического анализа необходимы иные наборы признаков, косвенно идентифицирующих тот или иной минерал. Если анализ интерпретируется как задача классификации, такие признаки именуются классификационными. Таким образом, нам необходим вектор признаков, значения которого, с одной стороны, позволяют максимально точно идентифицировать минерал, а с другой — могут быть оценены на основании информации, содержащейся в изображении образца руды.

В нашей работе в качестве классифицирующего признака использовались векторы изображений, полученные с помощью предобученной сверточной остаточной (residual) нейронной сети ResNet18 [1] . Отметим, что в качестве векторизатора могут рассматриваться и другие варианты сверточных сетей [9] , однако на задаче распознавания апатита уже ResNet18, с относительно небольшими количеством слоев и размером выходного вектора (512 компонентов), обеспечила достаточно высокое качество результата. Общая схема проведенных экспериментов представлена на рисунке 1.

Обучение

Разметка образцов

Секционирование

Векторизация

Обучение классификатора

Классификация

Изображение

Секционирование

Минералогическая разметка образца

Векторизация     Классификатор секций

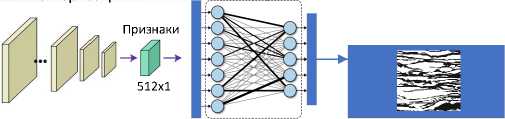
Рисунок 1. Общая схема экспериментов

В первой серии экспериментов изучалась эффективность использования векторизатора ResNet18 для идентификации ячеек планиметрической сетки с апатитом и прочими компонентами апатитовых руд различных типов. Задача интерпретировалась как задача бинарной классификации — для каждой ячейки планиметрической сетки необходимо определить принадлежность к положительному (апатит) или отрицательному (не-апатит) классам.

Для оценки возможности применения простых методов классификации, основанных на некоторой метрике в пространстве признаков, был проведен эксперимент по оценке близости векторов изображений различных размеров, полученных из фотографии одного размеченного образца. В качестве исходных данных взято изображение апатит-содержащей руды и соответствующая ей маска, представленные на рисунке 2 .

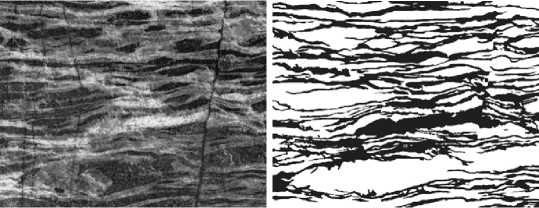
Рисунок 2. Использованное в эксперименте изображение апатитовой руды (слева) и соответствующая ему маска (справа)

На изображение была наложена планиметрическая сетка размером 50 x 50 пикселей со смещением, в результате получен набор из 902 объектов положительного и 4573 объектов отрицательного классов. Ячейки сетки, лежащие на границах минеральных пятен, из рассмотрения исключены. В качестве метрики близости объектов использовалось косинусное расстояние между векторами секций изображения, полученными с помощью ResNet18 (слой «Global Average Pool»).

Далее случайным образом был выбран эталонный объект класса «апатит» и относительно его векторного представления рассчитаны косинусные расстояния до объектов положительного и отрицательного классов. Диапазон расстояний между эталоном и объектами положительного класса составил: 0,75–0,98 со средним значением 0,8855. Аналогичный диапазон для объектов отрицательного класса составил 0,46–0,91 со средним значением 0,7523.

Мы видим, что объекты отрицательного и положительного классов могут быть достаточно близки по косинусному расстоянию. Таким образом, непосредственное использование в качестве классификационного признака дистанции в пространстве векторов, полученных с помощью ResNet18, не эффективно. Вместе с тем, хорошая разделимость объектов, полученная с помощью РСА2 (в силу ограниченности объема, эти эксперименты в данной статье не рассмотрены), указывает на возможность тренировки достаточно точного нейросетевого классификатора.

Для проверки этой возможности проведен эксперимент по бинарной классификации планиметрических ячеек с помощью ИНС прямого распространения. Использовались несколько эталонных (размеченных) образцов апатитовой руды с различной морфологией, классификатор тренировался на изображениях одних типов руд и тестировался на других. Это обеспечило наряду с кроссвалидацией проверку на внешних данных.

Задача распознавания апатита на изображениях руды также решалась как задача бинарной классификации фрагментов изображения. Для получения образцов данных, используемых для обучения модели, на исходные изображения накладывалась планиметрическая сетка с ячейкой 10 x 10 пикселей. Каждый образец затем получал бинарную метку («апатит/не-апатит») в соответствии с имеющейся маской. Пограничные образцы, маска которых содержала количество черных или белых пикселей менее заданного порога, из выборки исключались (рисунок 3) .

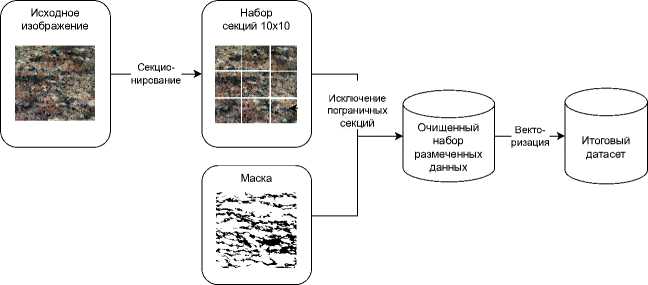
Рисунок 3. Схема формирования датасета для обучения бинарного классификатора

В соответствии с содержанием ПК (см. таблицу 1) , для большинства исходных изображений имело место разбалансирование выборки

(преобладание класса «не-апатит» в образцах). Для балансировки выборки в проведенных экспериментах использовалась субдискретизация (under-sampling) [19] методом случайного сокращения мажоритарного класса.

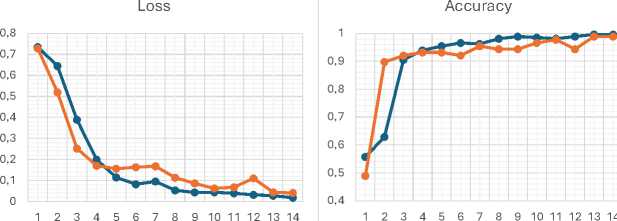
Классификатор тренировался на трех разных выборках, полученных из образцов (a), (b) и на всех изображениях, за исключением образца (c). Использовалась ИНС прямого распространения с пятью полносвязными слоями: начальный слой принимает 512-мерные векторы ResNet18, с последующими нелинейными преобразованиями через слои с активациями softmax, relu и sigmoid. Выходной слой имеет одну нейронную единицу с активацией sigmoid, интерпретируемую как вероятность принадлежности объекта положительному классу. Сеть обучена с использованием функции потерь binary-crossentropy и оптимизатора Adam. Общее количество тренируемых параметров: 618660. Кривые точности и функции потерь на обучающей и валидационной выборке представлены на рисунке 4.

—•—обучение —•—валидация           —•—обучение —•—валидация

Рисунок 4. Кривые точности и функции потерь на обучающей и валидационной выборке

Наряду с валидационной частью выборки, полученные классификаторы тестировались также на внешних данных, в качестве которых выступали изображения образцов руды, не участвовавшие в обучении. Результаты тестирования (оценивалась точность классификации) представлены в таблице 2.

Результаты показывают, что нейросетевой классификатор хорошо справляется с идентификацией апатита в рамках одного типа руды или некоторого набора руд со схожими морфологическими признаками. Вместе

Таблица 2. Результаты экспериментов с классификатором, обученным на образцах (a), (b) и на всех изображениях

Образец Точность (Precision), % Классификатор, обученный на образце (b) Классификатор, обученный на образце (a) Классификатор, обученный на всех образцах, исключая (с) b U •      аЛШ.-^*    ■<_ 99,87 a 93,776 98,5 d 95,071 85,417 e гч^. .у х ' 93,532 51,087 a FW^^ 59,77 98,64 c 38,552 36,471 98,824 a Жирным выделены оценки точности на валидационной части обучающей выборки.

с тем, добавление в обучающую выборку изображений различных типов руд не снижает точность классификации.

Для оценки влияния на эффективность классификации размера ячейки планиметрической сетки была проведена тренировка и тестирование классификаторов на датасетах, сформированных аналогичным описанному выше образом из всех имеющихся размеченных изображений, с размерами ячейки 2x2, 5x5, 10x10 и 20x20 пикселей. Выборки с малым размером были искусственно расширены путем смещения планиметрической сетки и вращения ячеек. Для исключения влияния размера датасетов для различных размеров ячейки используемые для тренировки наборы данных были выровнены путем случайного отбора равного количества объектов положительного и отрицательного классов (по 50 тысяч экземпляров каждого класса). Результаты экспериментов приведены в таблице 3.

Таблица 3. Эффективность бинарной классификации при различных размерах ячейки

Размер ячейки	2x2	5x5	10x10	20x20
Точность классификации на валида-ционной части выборки	0,7771	0,9023	0,9863	0,9994

Как видим, точность классификации предсказуемо растет с увеличением размера ячейки. Это можно объяснить более полной представленностью морфологических признаков минерала при большем размере ячейки (читай — большем размере изображения минерала). Верхнее ограничение размера ячейки, на практике, обусловливается физическим размером минеральных пятен.

Таким образом, использование нейросетевого векторизатора ResNet18 (без дообучения и модификации архитектуры) обеспечивает возможность эффективной бинарной классификации минерала апатит. Точность идентификации апатита приближается к единице уже при размере ячейки 20 x 20 пикселей и является достаточно высокой и при меньших размерах ячейки.

Для определения удельного содержания ПК в образце руды в целом необходимо учитывать как «чистые» представители позитивного и негативного классов, так и «пограничные» объекты. Далее в статье рассмотрены два варианта решения этой задачи: (1) интерпретация значений выходов бинарного классификатора как степеней принадлежности к классу и (2) мультиклассовая классификация.

Для проверки возможности непосредственного использования бинарного классификатора в задаче мягкой классификации с последующей интерпретацией значения принадлежности классу как удельного содержания искомого минерала использовалось размеченное изображение апатита повышенного разрешения с размером секции 20x20 пикселей. Бинарному нейросетевому классификатору, натренированному на размеченном датасете, включающем объекты положительного и отрицательного классов, были предъявлены 99 пограничных объектов с различным содержанием минерала, представляющих промежуточный класс. В результате, классификатор показал тенденцию к однозначному отнесению объекта к положительному классу при удельном содержании целевого минерала в нем 50% и более. Расчетное значение предсказанного содержания ПК в рассмотренных пограничных объектах, вычисленное по формуле (1), составило 0,84, при истинном значении 0,55. Таким образом, возможность непосредственной интерпретации выходных значений бинарного классификатора как степеней принадлежности классу (при использованной архитектуре и технологии обучения нейросетевого классификатора) не подтвердилась.

Для исследования эффективности решения задачи в мультиклассовой постановке осуществлялась тренировка многоклассовых нейросетевых классификаторов на имеющихся размеченных изображениях апатитовой руды, представленных в таблице 1. Множество объектов классификации формировалось путем наложения на изображения квадратной планиметрической сетки размером 10 x 10 пикселей. Были проведены две серии экспериментов с количеством классов 4 и 10. Границы классов определялись путем равномерного деления интервала удельного содержания ПК на 4 и 10 отрезков, соответственно. В полученных выборках доминировали объекты граничных классов, поэтому была произведена балансировка обучающей выборки методом чересстрочного удаления данных избыточного класса. Для увеличения количества объектов в миноритарных классах обучающей выборки также использовалась аугментация данных путем смещения планиметрической сетки на 5 пикселей, за счет чего обеспечено удвоение размера классов с малым количеством объектов. Общее число объектов обучающей выборки составило 12892.

В таблице 4 представлены параметры качества классификации, полученные в экспериментах с четыльмя классами. Можно отметить

Таблица 4. Параметры качества классификации для четырёх классов

Класс 1 2 3 4 Macro Micro Содержание ПК 0,75–1 0,5–0,75 0,25–0,5 0–0,25 Average Average Recall 0,635 0,718 0,678 0,738 0,692 0,691 Precision 0,813 0,340 0,335 0,707 0,549 0,453 Accuracy 0,872 0,531 0,575 0,877 0,691 n/a Weighted Precision 0,842 0,629 0,751 0,896 0,780 0,755 ожидаемо худшую точность классификации промежуточных классов (класс 2 и класс 3) в сравнении с пограничными классами. В целом низкая усредненная точность классификации, вычисленная без учета специфики классов в рассматриваемой задаче, и достаточно высокая взвешенная оценка точности объясняется тем, что большая часть ошибок классификатора происходит между соседними классами.

Для экспериментов с 10 классами получены схожие параметры качества классификации.

Для проверки эффективности многоклассовой классификации в задаче определения удельного содержания ПК в руде обученным классификаторам были предъявлены полные выборки объектов, полученные путем наложения планиметрической сетки на имеющиеся образцы изображений. Размер полных выборок составил 31850 и 126700 объектов для экспериментов с четырьмя и десятью классами, соответственно (больший размер выборки для 10 классов обеспечен аугментацией набора данных путем последовательного смещения планиметрической сетки на 5 пикселей).

Предсказанный удельный объем ПК по всему набору объектов вычислялся по формуле (3) . Значения усредненного удельного содержания ПК для каждого класса (параметр c i ) приведены в таблице 5 .

Таблица 5. Параметр c i для различных классов

Класс	1	2	3	4	5	6	7	8	9	10
4 класса	0,875	0,625	0,375	0,125	-	-	-	-	-	-
10 классов	0,95	0,85	0,75	0,65	0,55	0,45	0,35	0,25	0,15	0,05

Фактическое содержание ПК по всей выборке составляло 37,24%. Предсказанные значения содержания ПК при использовании 4-классового и 10-классового классификаторов составили 45,6% и 39,54% соответственно. Величина абсолютной ошибки, таким образом, составила 8,5% для 4-классового и 2,3% для 10-классового классификаторов. В таблице 6 представлены результаты применения 10-классового классификатора для определения удельного содержания ПК в каждом образце руды и по всей выборке в целом.

По экспертным оценкам, опытный рудничный геолог способен без использования инструментальных методов анализа оценить удельное содержание апатита в руде с абсолютной ошибкой до 8%. Таким образом, многоклассовая классификация обеспечивает точность определения содержания ПК, сопоставимую с точностью экспертных оценок, а при достаточно большом количестве классов—значительно превышающую таковую.

Таблица 6. Результаты применения многоклассовой классификации для определения удельного содержания ПК в образцах

Индекс	a	b	c	d	e	a–e
Образец			IB
Фактическое содержание ПК, %	31,45	39,14	50,30	40,63	24,69	37,24
Предсказанное содержание ПК, %	36,44	43,66	48,59	38,45	30,55	39,54
Абсолютная ошибка, %	4,99	4,52	1,71	2,18	5,85	2,30

Заключение

В работе исследована возможность и эффективность реализации планиметрического минералогического анализа как задачи классификации с использованием методов машинного обучения. Предложены и проанализированы, в применении к рассматриваемой прикладной задаче, формальные постановки и потенциальная эффективность задач мягкой, бинарной и мультиклассовой классификации. Экспериментальная проверка эффективности предложенных подходов осуществлена на примере пяти различных видов апатитовых руд Хибинского месторождения.

Эксперименты показали высокую эффективность использования предобученной ИНС ResNet18 для извлечения из изображений, полученных обычной камерой, классификационных признаков целевого минерала. Причем использованный признаковый вектор обеспечивает высокую точность классификации даже при относительно малых размерах ячейки планиметрической сетки и существенно деградирует лишь при размере секции 2 x 2 пикселя.

Реализация планиметрического анализа как задачи классификации в различных постановках показала, что применение мультиклассового классификатора обеспечивает точность определения удельного содержания целевого минерала в образцах, сопоставимую с точностью экспертных оценок опытным рудничным геологом. При этом планиметрический подход к минералогическому анализу руд представляется более универсальным и менее требовательным к качеству обучающих данных и сложности используемых моделей и технических средств в сравнении с подходами на основе семантической сегментации изображений.

Несмотря на то, что в работе рассмотрен лишь один целевой минерал — апатит, результаты могут быть распространены и на задачи анализа других видов минеральных руд, изображения которых обладают свойствами однородности и смежности классов, сформулированными в данной статье. Следует отметить, что подобными свойствами могут обладать и изображения, анализируемые в контексте других прикладных задач, отличных от минералогического анализа. Это открывает возможности для использования аналогичного (планиметрического) подхода к решению широкого спектра задач анализа изображений, где требуется определять удельную площадь визуальных объектов некоторого класса. При этом могут использоваться любые источники исходных данных — от специализированных микроскопов до данных дистанционного зондирования Земли.